Методика решения задач

При решении задач на данную тему надо пользоваться общей методикой решения задач, но существуют тонкости, которые необходимо учитывать в этом разделе электромагнетизма. Порядок решения задач на нахождение индукции или напряженности магнитного поля от одного или нескольких источников магнитного поля следующий.

1. Записать условия задачи кратко и перевести все численные данные в единую систему единиц.

2. Нарисовать рисунок. При этом следует помнить, что индукция или напряженность магнитного поля – величины векторные, которые характеризуются как величиной, так и направлением.

3. Для изображения вектора магнитной индукции или напряженности магнитного поля необходимо нарисовать силовые линии магнитной индукции, проходящие через точку пространства, в которой необходимо определить магнитную индукцию, и изобразить их направление по правилу буравчика.

4. Вектор магнитной индукции, так же как и вектор напряженности поля будет совпадать с касательной к силовым линиям в данной точке.

5. Если поле создается несколькими проводниками с током или несколькими частями проводника с током, имеющим сложную геометрию, то результирующую магнитную индукцию или напряженность следует искать по принципу суперпозиции как векторную сумму всех напряженностей или магнитных индукций поля..

6. Величину каждой магнитной индукции или напряженности определяют апо закону Био-Савара-Лапласа в соответствии с геометрией проводника.

Примеры решения задач

Задача 1. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I₁ = 60 А и I₂ = 30 А, расположены на расстоянии d = 10 см друг от друга в воздухе . Определить магнитную индукцию B в точках:

1. А₁, расположенной между проводниками с током на расстоянии d/2 от каждого из них;

2. А₂, расположенной на расстоянии d/2 от проводника с током I₁ и на расстоянии 3d/2 от проводника с током I₂;

3. А₃,, расположенной на расстоянии R₁ = 5 см от первого тока и на расстоянии R₂ = 12 см от второго тока.

I ₁ = 60 А Найдем магнитную индукция в точке А₁.

I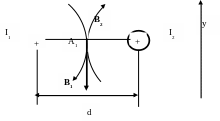 ₂ = 30 А Для этого нарисуем рисунок.

R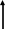 ₁ = 5 см = 5^.10^-2 м

R₂ = 12 см = 12^. 10^-2 м

d = 10 см = 10^-1 м

B = ?

Согласно принципу суперпозиции

B = B₁ + B₂

В проекции на выбранную ось y это уравнение примет вид:

B = B₂ – B₁.

прямого бесконечно длинного провода

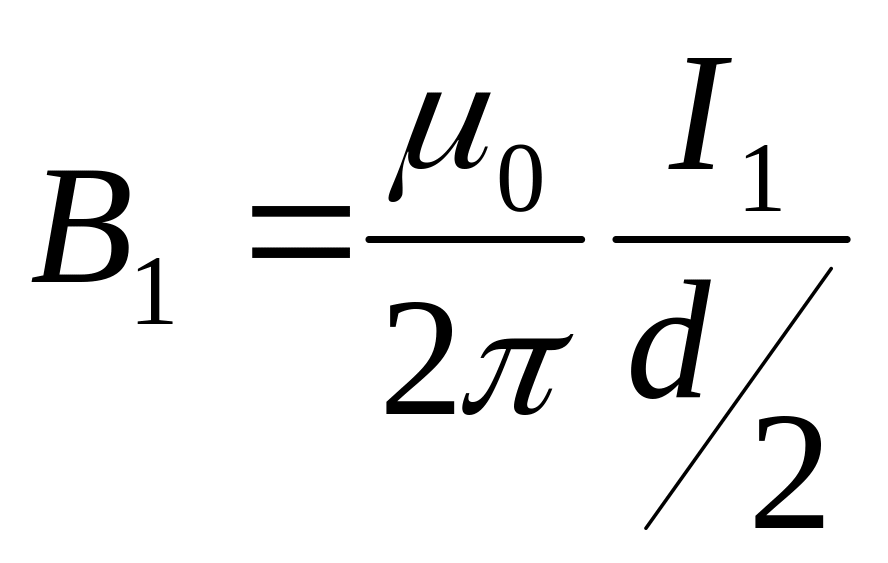
Подставив численные значения величин, получим значение магнитной индукции в точке А_1..

B = - 120 мкТл

Знак минус означает, что направление результирующей магнитной индукции противоположно выбранной оси y.

Найдем магнитную индукция в точке А₂

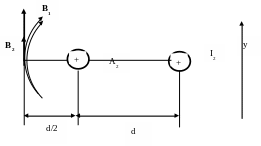
I₁

По принципу суперпозиции магнитная индукция в точке А₂ равна

B = B₁ + B_2,

а в проекции на ось y это уравнение примет вид:

B = B₁ + B₂.

Величина магнитной индукции от первого и второго тока определяется по закону Био-Савара-Лапласа для прямого бесконечно длинного проводника с током:

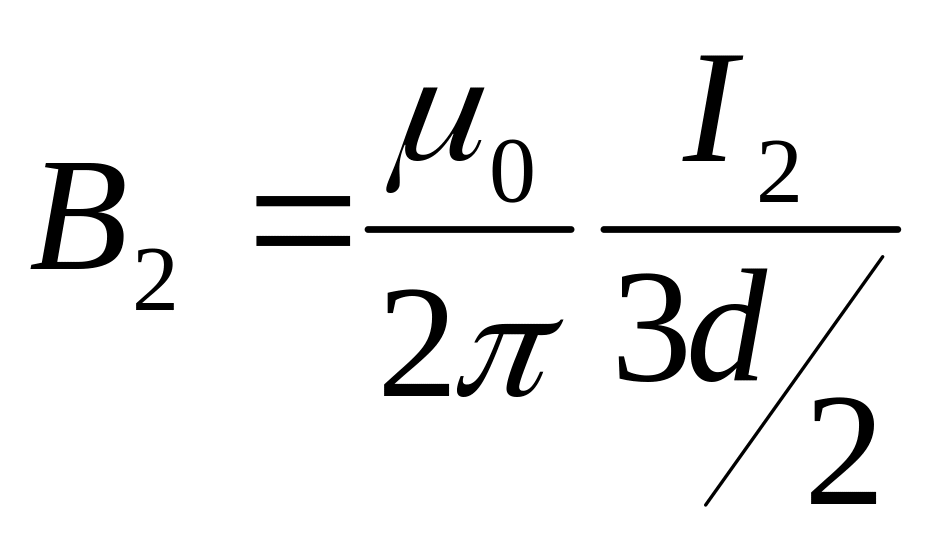
Подставив численные значения величин, получаем:

B=200 мкТл.

Найдем магнитную индукция в точке А_3.

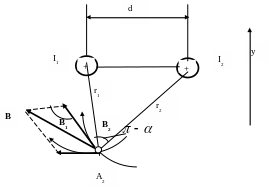
По принципу суперпозиции результирующая магнитная индукция равна векторной сумме магнитных индукций:

B = B₁ + B₂

Модуль результирующей магнитной индукции можно получить по теореме косинусов:

,

где  - угол между векторами B₁ и B_2. Cos  из геометрического треугольника:

Величины каждой магнитной индукции получим из закона Био-Савара-Лапласа для прямого бесконечно длинного проводника с током:

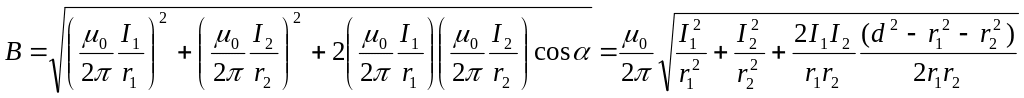
Подставив численные значения, получим:

B =

Задача 2. Длинный провод с током I = 50 А изогнут под углом =2/3 и находится в воздухе. Определить магнитную индукцию в точке А₁, находящуюся на продолжении одной из сторон угла на расстоянии d = 5 см от его вершины, и в точке А₂,, находящейся на биссектрисе угла на расстоянии d = 5 см от его вершины.

Д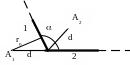 ля определения индукции магнитного поля в точке А₁ нужно разбить фигуру на два участка 1 и 2. По принципу суперпозиции результирующая магнитная индукция будет равна векторной сумме магнитных индукция от первого и второго участков провода:

Магнитная индукция В₂ = 0, как следует из закона Био-Савара-Лапласа ,согласно которому в точках, лежащих на оси проводника dВ = 0 ( ).Магнитную индукцию B₂ найдем, воспользовавшись формулой закона Био-Савара-Лапласа для проводника конечной длины с несимметричной точкой, в которой ищем магнитную индукцию,

Для этого надо найти величину r₀ – кратчайшего расстояния от точки до проводника.

,

Для точки А₁ магнитная индукция равна:

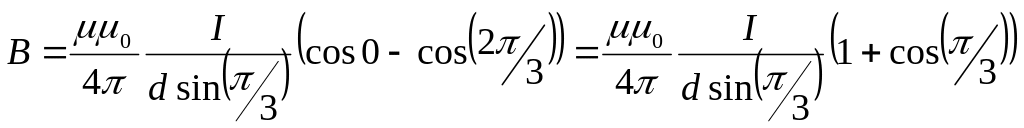
B = 17 мТл.

Найдем магнитную индукцию в точке А₂. По принципу суперпозиции В = В₁ + B₂/ По правилу буравчика магнитная индукция будет лежать вдоль прямой, перпендикулярной плоскости чертежа, и направлена на нас.

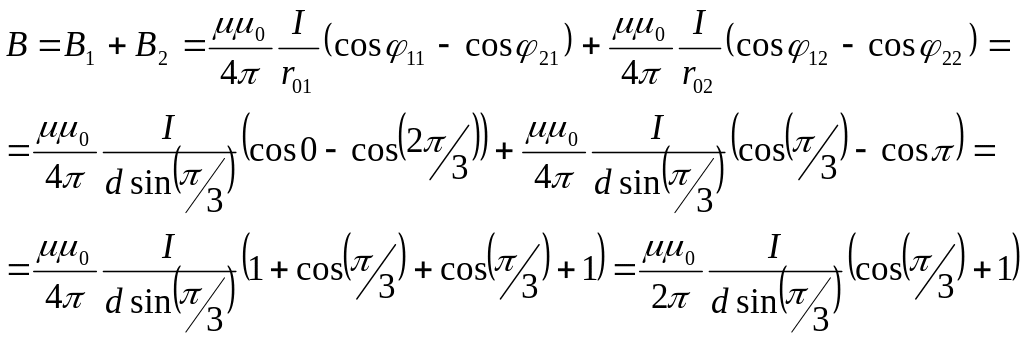
B = 35 мТл.

Задача3.Бесконечно длинный проводник, находящийся в воздухе, изогнут так, как это показано на рисунке. Радиус дуги R = 10 см. Определить магнитную индукцию поля, создаваемого в точке О током I = 80 А, текущем в этом проводнике.

I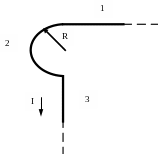 = 80 А

R = 0,1 м

B = ?

Рисунок

Для решения задачи разделим проводник на три участка. Тогда по принципу суперпозиции результирующая индукция поля будет равна векторной сумме магнитных индукций от каждого участка. Применив правило буравчика для каждого участка проводника можно увидеть, что все они направлены вдоль прямой, перпендикулярной плоскости чертежа на нас и следователь векторное сложение можно заменить скалярным сложением: B = B₁ + B₂ + B₃ Причем B₃ = 0 (см. предыдущую задачу).Найдем индукцию магнитного поля для каждого участка

B = 4,14 мкТл.

Задача 4.По тонкому проводящему кольцу, находящемуся в воздухе, радиуса R = 10 см течет ток I = 80 А. Найти магнитную индукцию в точке А, Равноудаленной от всех точек кольца на расстояние, а = 20 см.

R = 0,1 м Для решения задачи воспользуемся законом Био-Савара-Лапласа:

I = 80 А ,

а = 0,2 м где dB – магнитная индукция поля, создаваемого элементом тока Idl в точке, определяемой радиусом-вектором r.

B = ?

Выделим на кольце элемент dI и от

него в точку А проведем радиус-вектор r. Вектор dB направим в

с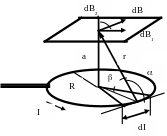 оответствии с правилом буравчика.

Согласно принципу суперпозиции

Магнитных полей, магнитная

индукция B в точке А определяется

интегралом

,где

Разложим вектор dB на две

составляющие: перпендикулярную

плоскости кольца dB₂ и

параллельную этой плоскости dB₁.

Тогда

Заметив, что из соображений симметрии и что от различных элементов dl сонаправлены, заменим векторное суммирование (интегрирование) скалярным:

(поскольку dl перпендикулярен r и, следовательно ). Таким образом,

; ;

Окончательно получим

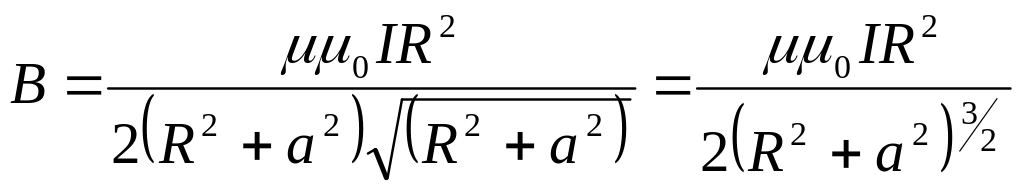
Подставив численные значения, получим

B = 6,3 мкТл.

Задача 5.Определить магнитную индукцию поля, созданного соленоидом длиной L=5 см и радиусом витка R =2 см , в точке, отстоящей от конца соленоида на расстояние а = 0,5 см, если по соленоиду протекает ток I = 50 А.Cоленоид имеет N =20 витков.

R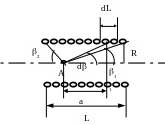 = 0,02 м = 2^.10^-2 м

L = 0,05 м = 5^.10^-2 м

а = 0,005 м = 5^.10^-3 м

I = 50 А

Рассчитаем магнитную индукцию в точке А.Для этого выберем на соленоиде элемент dL, содержащий n = N/L витков на единицу длины. При токе I его можно рассматривать как круговой ток IndL, для которого магнитная индукция равна (см. предыдущую задачу):

,

так как

, и

Окончательно получаем:

,

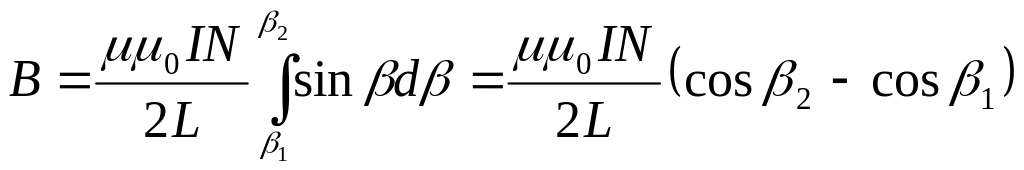где и

Подставив численные значения, получим B = 2,5 мТл.