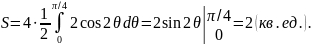- •Элементы интегрального исчисления функций одной переменной л.С. Маергойз
- •§1. Предварительные сведения из курса дифференциального исчисления
- •§2. Неопределенный интеграл.
- •2.1. Понятие неопределенного интеграла и его свойства.
- •2.2. Замена переменной
- •2.3. Интегрирование по частям
- •2.4. Интегрирование рациональных функций
- •2.5. Интегрирование иррациональных функций
- •2.6. Интегрирование тригонометрических функций
- •§3. Определенный интеграл
- •3.1. Основные сведения об определенном интеграле
- •3.2. Правила вычисления определенных интегралов
- •Формула интегрирования по частям.
- •3.3. Несобственные интегралы
- •4. Вычисление площади плоской фигуры
- •§ 5. Приложение определенных интегралов к решению физических задач.
- •§ 6. Варианты расчетных заданий Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Оглавление
4. Вычисление площади плоской фигуры
1.
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
функции
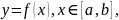 где
где
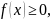 прямыми
,
прямыми
,
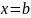 и
отрезком
оси
и
отрезком
оси
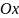 ,
вычисляется
по формуле
,
вычисляется
по формуле
Дадим доказательство формулы (17). Оно служит иллюстрацией метода решения прикладных задач на суммирование бесконечно малых величин.
◄ Пусть
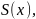 где
где
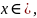 – площадь "переменной" криволинейной
трапеции, ограниченной графиком функции
– площадь "переменной" криволинейной
трапеции, ограниченной графиком функции
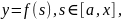 вертикальными прямыми
вертикальными прямыми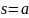 и
и
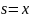 и отрезком
и отрезком
 оси
оси
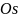 .
Значение S
= S(b)
функции S(x)
в точке b
– искомая
площадь заданной криволинейной трапеции.
.
Значение S
= S(b)
функции S(x)
в точке b
– искомая
площадь заданной криволинейной трапеции.
Покажем,
что функция
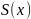 – первообразная для
Приращение
– первообразная для
Приращение
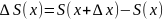 функции
при фиксированном
функции
при фиксированном
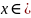 и достаточно малом
и достаточно малом
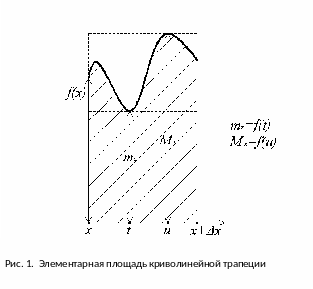
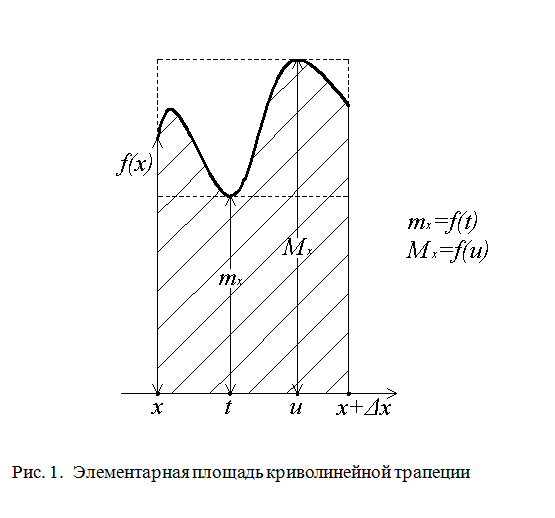
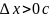 геометрической точки зрения представляет
собой “элементарную площадь криволинейной
трапеции” (см. рисунок 1). В данных на
этом рисунке обозначениях имеем:
геометрической точки зрения представляет
собой “элементарную площадь криволинейной
трапеции” (см. рисунок 1). В данных на
этом рисунке обозначениях имеем:
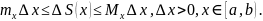
Здесь
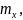
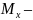 соответственно
минимум, максимум функции f
на отрезке [x,
x
+
],
причем
соответственно
минимум, максимум функции f
на отрезке [x,
x
+
],
причем
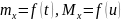 для
некоторых t,
u
[x,
x
+
]
(см. свойство 4 непрерывных функций).
Поэтому
для
некоторых t,
u
[x,
x
+
]
(см. свойство 4 непрерывных функций).
Поэтому
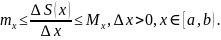
Последнее
неравенство верно и при
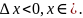 Далее поступаем по аналогии с рассуждениями
в пункте 2 доказательства формулы
Ньютона-Лейбница. Если
,
то
Далее поступаем по аналогии с рассуждениями
в пункте 2 доказательства формулы
Ньютона-Лейбница. Если
,
то
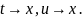 Поэтому, учитывая непрерывность функции
и переходя к пределу в найденном
неравенстве при
Поэтому, учитывая непрерывность функции
и переходя к пределу в найденном
неравенстве при
 приходим
к выводу
приходим
к выводу
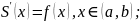
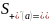
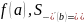
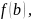 (*)
(*)
где
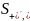
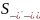 соответственно правая и левая производные
функции
соответственно правая и левая производные
функции
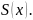
Без
ограничения общности можно считать,
что функция
задана на интервале
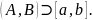 Например,
это выполняется, если вне отрезка
определить
так:
Например,
это выполняется, если вне отрезка
определить
так:
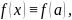 x
x
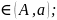
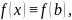 x
x
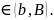
Для определения функции вне отрезка полагаем:
S(x) = (x - a) f (a), x S(x) = (x - b) f (b) + S(b), x
Отсюда
и из соотношения (*) заключаем, что в
точках a
и
b
правая
и левая производные функции
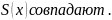 Поэтому справедливо равенство
Поэтому справедливо равенство
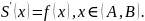
Итак,
функция
– одна из первообразных для
на
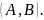 По формуле Ньютона-Лейбница получаем:
По формуле Ньютона-Лейбница получаем:
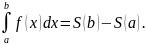
Но
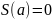 ,
а
,
а
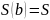 –
искомая площадь. Формула (17) доказана.
►
–
искомая площадь. Формула (17) доказана.
►
2.
Площадь
фигуры, ограниченной графиками непрерывных
функций
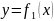 ,
,
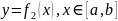 ,
где
,
где
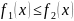 ,
и
прямыми
,
и
прямыми
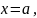
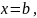
определяется по формуле
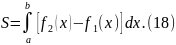
◄ Из
свойства 4 непрерывных функций, следует,
что
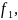
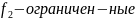 функции. Поэтому найдется постоянная
С
такая, что
функции. Поэтому найдется постоянная
С
такая, что
f
(x)
:=
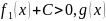 :=
:=
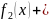 C
> 0 для всех
C
> 0 для всех
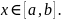
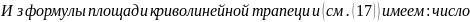
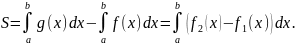
разность
площадей двух криволинейных трапеций,
определяемых графиками функций
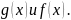 Поэтому оно равно площади фигуры,
отличающейся от рассматриваемой лишь
параллельным переносом. Т.е. формула
(18) верна. ►
Поэтому оно равно площади фигуры,
отличающейся от рассматриваемой лишь
параллельным переносом. Т.е. формула
(18) верна. ►
3.
Пусть кривая задана параметрическими
уравнениями
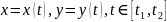 ,
где
,
где
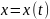 – монотонная
непрерывная функция, имеющая непрерывную
производную и такая что
– монотонная
непрерывная функция, имеющая непрерывную
производную и такая что
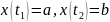 ,
а
,
а
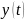 – непрерывная
функция со свойством
– непрерывная
функция со свойством
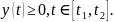 Тогда
площадь криволинейной трапеции,
ограниченной этой кривой, прямыми
и
отрезком
оси
,
выражается формулой
Тогда
площадь криволинейной трапеции,
ограниченной этой кривой, прямыми
и
отрезком
оси
,
выражается формулой
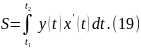
◄ У
монотонной непрерывной функции
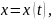
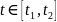 существует
непрерывная обратная функция
существует
непрерывная обратная функция
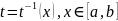 (см. свойство 5 непрерывных функций).
Из свойства 2 этих функций заключаем,
что непрерывной является и функция
(см. свойство 5 непрерывных функций).
Из свойства 2 этих функций заключаем,
что непрерывной является и функция
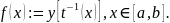 Искомая площадь определяется формулой
(17). Делая в этом интеграле замену
переменой
Искомая площадь определяется формулой
(17). Делая в этом интеграле замену
переменой
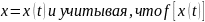 = y(t),
= y(t),
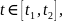 приходим к формуле (19). ►
приходим к формуле (19). ►
4.
Площадь S
криволинейной фигуры, ограниченной
кривой, заданной в полярных координатах
уравнением
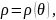 где
где
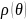 – непрерывная функция,
и
двумя полярными радиусами
– непрерывная функция,
и
двумя полярными радиусами
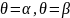 ,
,
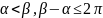 ,
находится по формуле
,
находится по формуле
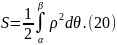
Доказательство этого равенства предоставляется читателю в качестве упражнения, опираясь на метод доказательства формулы (17).
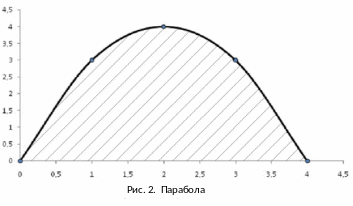
Пример
1. Найти
площадь S
фигуры, ограниченной параболой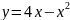 и осью
.
и осью
.
Парабола
пересекает ось
в точках
 и
и
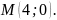 Следовательно, по формуле (17) имеем:
Следовательно, по формуле (17) имеем:
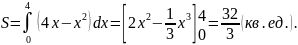
Пример
2. Найти
площадь фигуры, ограниченной параболой
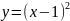 и гиперболой
и гиперболой
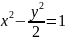 .
.
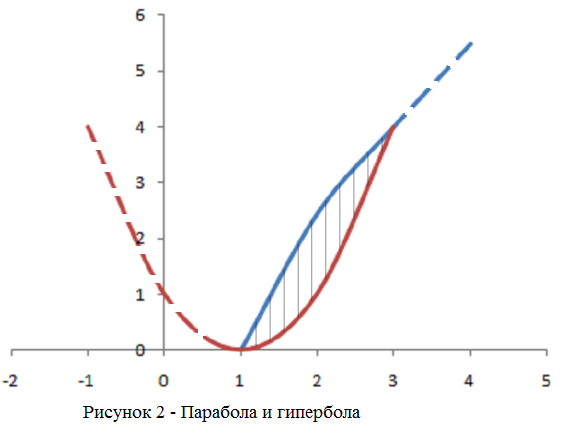
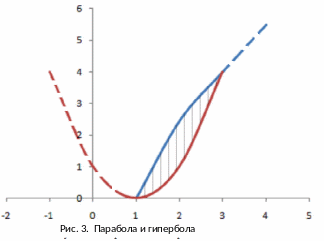
Найдем точки пересечения параболы и гиперболы, для этого решим систему уравнений:
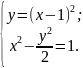
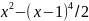 или
или
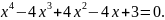
Левую
часть последнего уравнения можно
разложить на множители:
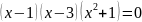 ,
откуда
,
откуда
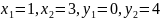 .
Таким
образом, заданные кривые пересекаются
в точках
.
Таким
образом, заданные кривые пересекаются
в точках
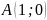 и
и
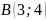 .
Отсюда, используя формулу
.
Отсюда, используя формулу
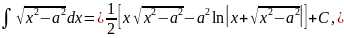
получаем (см. (18))
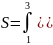

Пример
3. Вычислить
площадь плоской фигуры, ограниченной
одной аркой циклоиды 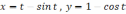 и осью
и осью 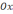 ,
,
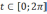 .
.
Здесь
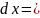 ,
а
,
а
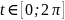 .
Поэтому по формуле (17) находим:
.
Поэтому по формуле (17) находим:
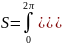
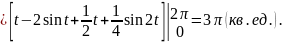
Здесь
использовалась формула
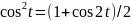 .
.
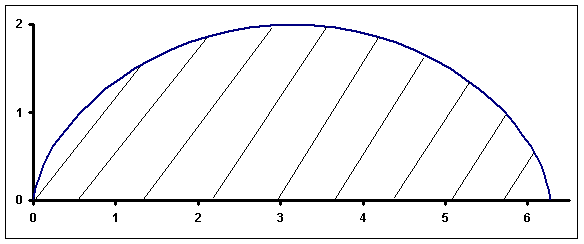
Рис.4. Арка циклоиды
Пример
4. Найти
площадь плоской фигуры, ограниченной
лемнискатой
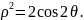
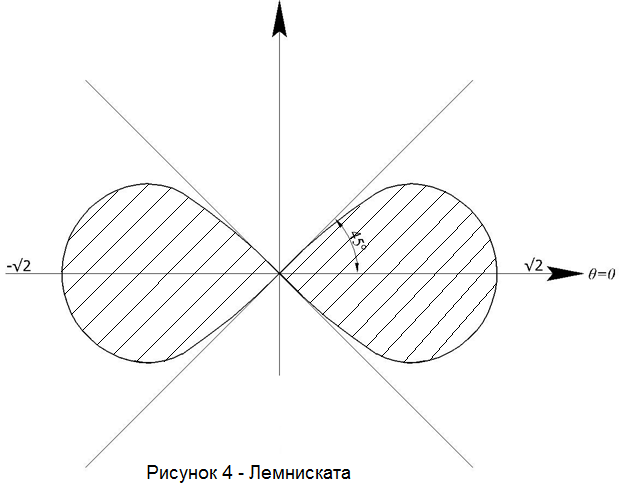
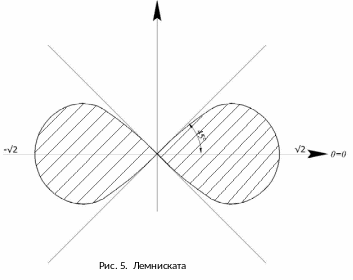
Четвертая
часть искомой площади фигуры расположена
между полярными радиусами
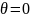 и
и
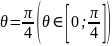 .
Из
(20) имеем:
.
Из
(20) имеем: