- •Элементы интегрального исчисления функций одной переменной л.С. Маергойз
- •§1. Предварительные сведения из курса дифференциального исчисления
- •§2. Неопределенный интеграл.
- •2.1. Понятие неопределенного интеграла и его свойства.
- •2.2. Замена переменной
- •2.3. Интегрирование по частям
- •2.4. Интегрирование рациональных функций
- •2.5. Интегрирование иррациональных функций
- •2.6. Интегрирование тригонометрических функций
- •§3. Определенный интеграл
- •3.1. Основные сведения об определенном интеграле
- •3.2. Правила вычисления определенных интегралов
- •Формула интегрирования по частям.
- •3.3. Несобственные интегралы
- •4. Вычисление площади плоской фигуры
- •§ 5. Приложение определенных интегралов к решению физических задач.
- •§ 6. Варианты расчетных заданий Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Оглавление
§2. Неопределенный интеграл.
Объектом
внимания в этом разделе является функция
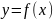 ,
заданная на интервале
,
заданная на интервале
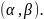
2.1. Понятие неопределенного интеграла и его свойства.
Функция
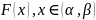 называется первообразной
для
функции
называется первообразной
для
функции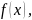
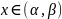 ,
если
,
если
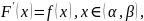
т.
е. в каждой точке интервала
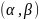 значение функции
значение функции
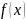 совпадает
с производной функции
совпадает
с производной функции
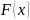 в
той же точке.
в
той же точке.
Теорема.
Любые
две первообразные
и
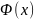 для функции
для функции
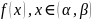 отличаются на некоторую постоянную
величину, т. е.
отличаются на некоторую постоянную
величину, т. е.
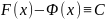 ,
где C = const.
,
где C = const.
◄Рассмотрим
функцию
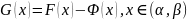 .
Тогда из определения понятия первообразной
получаем
.
Тогда из определения понятия первообразной
получаем
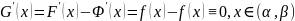 .
.
Зафиксируем
точку
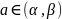 .
Учитывая свойство производной функции
G
и
используя формулу Лагранжа с замечанием
к ней, имеем для каждой точки
.
Учитывая свойство производной функции
G
и
используя формулу Лагранжа с замечанием
к ней, имеем для каждой точки
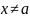 этого
интервала:
этого
интервала:
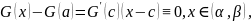
где
c
– некоторая точка интервала
,
расположенная между точками a
и x.
Это означает, что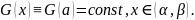 ►
►
В дальнейшем для простоты изложения опускается область определения функций и их первообразных.
Определение.
Совокупность всех первообразных для
заданной функции
называется неопределенным
интегралом от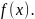 Эта совокупность обозначается
символом
Эта совокупность обозначается
символом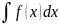 (читается:
интеграл
(читается:
интеграл
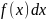 ).
).
Поскольку,
согласно теореме, все функции этой
совокупности отличаются на постоянную
величину, то для нахождения
достаточно
знать одну первообразную
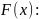
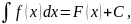
где
C
– произвольное число. При этом,
называют подынтегральной
функцией,
а
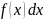 - подынтегральным
выражением (дифференциальной
формой).
Фактор
называют
переменной
интегрирования.
Процесс отыскания неопределенного
интеграла называют интегрированием
функции.
- подынтегральным
выражением (дифференциальной
формой).
Фактор
называют
переменной
интегрирования.
Процесс отыскания неопределенного
интеграла называют интегрированием
функции.
Свойства неопределенного интеграла (правила интегрирования)
1)

2)
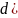
3)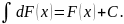
4)
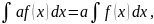 где
где
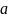 - постоянная.
- постоянная.
5)
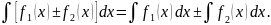
6)
Если функция
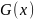 является произведением сложной функции
является произведением сложной функции
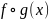 и производной
внутренней функции
,
а
и производной
внутренней функции
,
а
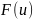 – первообразная внешней функции
,
то
– первообразная внешней функции
,
то
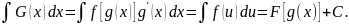
Таблица основных интегралов
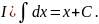 IX)
IX)
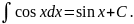
II)
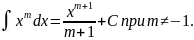 X)
X)
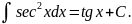
III)
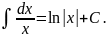 XI)
XI)
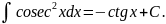
IV)
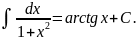 XII)
XII)
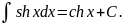
V)
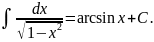 XIII)
XIII)

VI)
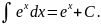 XIV)
XIV)
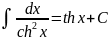
VII)
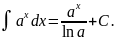 XV)
XV)
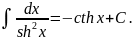
VIII)
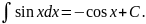
Здесь
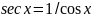 ,
,
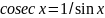 ,
,
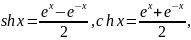
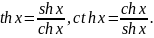
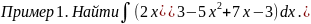
Используя свойства 4) и 5), получаем
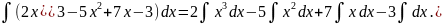
К первым трем интегралам в правой части применим формулу II), а к четвертому интегралу – формулу I):
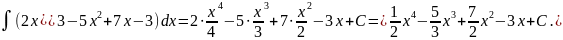
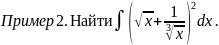
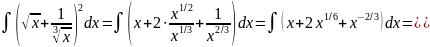
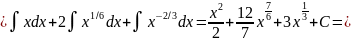
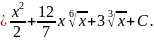
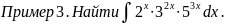
Используя формулу VII), получаем
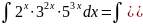
2.2. Замена переменной
Один из способов вычисления интегралов связан с заменой переменной в подынтегральном выражении.
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
1)
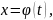 где
где
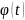 – монотонная, непрерывно дифференцируемая
функция новой переменной
– монотонная, непрерывно дифференцируемая
функция новой переменной
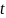 .
Формула замены переменной в этом случае
имеет вид
.
Формула замены переменной в этом случае
имеет вид
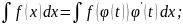
2)
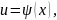 где
где
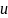 - новая переменная, а функция
представима в виде
- новая переменная, а функция
представима в виде
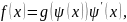
т.
е. подынтегральная функция – это
произведение сложной функции, где
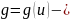 внешняя функция,
внешняя функция,
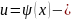 внутренняя функция,
внутренняя функция,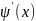 – ее производная. Формула замены
переменной при такой подстановке имеет
вид (см. свойство 6) интегралов):
– ее производная. Формула замены
переменной при такой подстановке имеет
вид (см. свойство 6) интегралов):
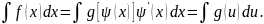
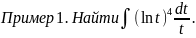
Выражение
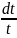 можно записать как
,
поэтому из свойства 6) интегралов и
формулы II)
находим
можно записать как
,
поэтому из свойства 6) интегралов и
формулы II)
находим

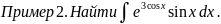
Заданный интеграл можно представить как:
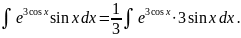
Учитывая,
что
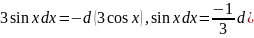 ,
имеем из свойства 4)
,
имеем из свойства 4)
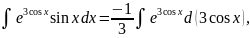
т.
е. новой переменной интегрирования
является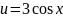 .
Следовательно, интеграл вычисляется с
помощью свойства 6), в котором
.
Следовательно, интеграл вычисляется с
помощью свойства 6), в котором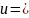
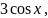 F(u)
=
F(u)
=
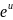 и формулы VI):
и формулы VI):
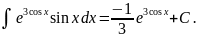
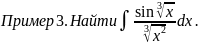
Воспользуемся
подстановкой
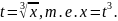 Эта подстановка приведет к тому, что
под знаком синуса окажется новая
переменная интегрирования
.
Найдем дифференциал
Эта подстановка приведет к тому, что
под знаком синуса окажется новая
переменная интегрирования
.
Найдем дифференциал
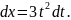 Отсюда имеем (см. формулу VIII))
Отсюда имеем (см. формулу VIII))
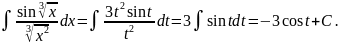
Ответ
нужно выразить через старую переменную
.
Подставляя в результат интегрирования
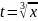 ,
получим
,
получим
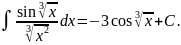
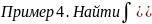
Полагая
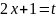 ,
имеем
,
имеем
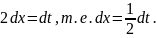 Отсюда получим
Отсюда получим
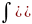
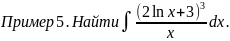
Так
как производная выражения
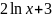 равна
равна
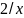 ,
а второй множитель 1/x
отличается от этой производной только
постоянным коэффициентом 2, то нужно
применить подстановку
,
а второй множитель 1/x
отличается от этой производной только
постоянным коэффициентом 2, то нужно
применить подстановку
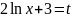 .
Тогда
.
Тогда
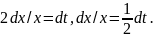 Следовательно,
Следовательно,
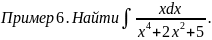
Преобразуя
знаменатель дроби, получим
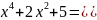 Воспользуемся подстановкой
Воспользуемся подстановкой
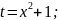 тогда
тогда
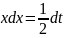 .
Отсюда
.
Отсюда
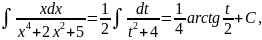
учитывая что,
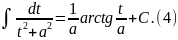
Таким образом,
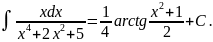

Положим
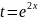 ,
тогда
,
тогда
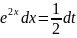 .
Используя формулу (4), находим
.
Используя формулу (4), находим