
- •Курсовая работа
- •Системы координат, применяемые в геодезии.
- •1.1. Система прямоугольных пространственных координат (X,y,z).
- •1.2.Система геодезических пространственных координат (b,l,h).
- •1.3. Система геоцентрических широт и геодезических долгот (ф,l).
- •1.4. Система плоских прямоугольных координат Гаусса-Крюгера (X,y).
- •Технологические схемы преобразования координат из одной системы в другую.
- •Вычисление пространственных прямоугольных координат по геодезическим координатам.
- •Вычисление плоских прямоугольных координат Гаусса-Крюгера по геодезическим координатам.
- •Местная система плоских прямоугольных координат Гаусса-Крюгера.
1.2.Система геодезических пространственных координат (b,l,h).
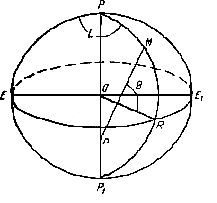
Рис .1.2.
Геодезической широтой точки М называется острый угол В, образованный нормалью Мп к поверхности эллипсоида в данной точке и плоскостью экватора ERE1 .
Геодезическая широта обозначается буквой В. Широты отсчитываются от экватора к северу и югу и называются, соответственно, северными и южными широтами. Пределы измерения от 00 до 900.
Геодезическая долгота L точки М - двугранный угол РМР1Е, образованный плоскостью начального меридиана РЕР1 и плоскостью меридиана данной точки.
Долгота измеряется от 00 до 3600 или от 00 до 1800 на восток и запад от гринвичского меридиана.
В качестве начального меридиана для счета долгот в настоящее время повсеместно принят меридиан, проходящий через Гринвичскую обсерваторию.
Геодезическая высота Н – отрезок нормали к поверхности эллипсоида вращения, заключенный между этой поверхностью и данной точки.
Иначе говоря, предварительно редуцируя результаты измерений на поверхность референц-эллипсоида, мы приводим их к нулевой высоте (Н — 0). Этим существенно упрощается решение геодезических задач: от вычисления трех координат (B, L, H), определяющих положение точки в пространстве, переходят к вычислению двух (B, L). Это целесообразно для точек земной поверхности, для которых Н всегда мало, а следовательно малы и редукции. При значительных высотах Н указанное редуцирование измеренных величин становится нецелесообразным, чем и вызывается необходимость перехода в этом случае к системе пространственных прямоугольных координат.
Достоинства системы:
Едина для всей поверхности эллипсоида и, таким образом, объединяет в общей для всей земной поверхности координатной системе геодезические, съемочные и картографические материалы.
Геодезическая широта и долгота определяют положение нормали к эллипсоиду, проходящей через данную точку.
) Координатные линии в этой системе (параллели и меридианы) являются основными линиями любой картографической проекции.
Недостатки системы:
Сложность решения всех геодезических задач.
Из-за необходимости редуцирования результатов на поверхность эллипсоида накладно использовать для обработки результатов спутниковых наблюдений.
1.3. Система геоцентрических широт и геодезических долгот (ф,l).
Одной из координат в этой системе является геодезическая долгота L, которая определяет меридианный эллипс, проходящий через точку М. Положение точки М на этом эллипсе в рассматриваемой системе координат определяется геоцентрической широтой Ф. Геоцентрическая широта определяется как угол между радиусом-вектором р точки М и плоскостью экватора или, что все равно, большой полуосью меридианного эллипса. На рис.1.3. ОМ — радиус-вектор р меридианного эллипса, проведенного через точку М; угол МОЕ1 — геоцентрическая широта Ф точки М.
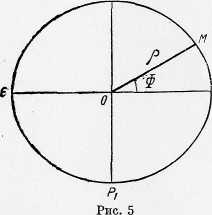 Рис.1.3.
Рис.1.3.
Эта система координат в высшей геодезии применяется редко; чаще в астрономии, теории фигуры Земли и математической картографии.
Достоинства системы:
Позволяет однозначно определить положение точки в пространстве.
В этой системе координат иногда формулы сфероидической геодезии записываются короче, выглядят проще, чем формулы геодезической.
Эта система имеет вспомогательные значения.
