
- •Курсовая работа
- •Системы координат, применяемые в геодезии.
- •1.1. Система прямоугольных пространственных координат (X,y,z).
- •1.2.Система геодезических пространственных координат (b,l,h).
- •1.3. Система геоцентрических широт и геодезических долгот (ф,l).
- •1.4. Система плоских прямоугольных координат Гаусса-Крюгера (X,y).
- •Технологические схемы преобразования координат из одной системы в другую.
- •Вычисление пространственных прямоугольных координат по геодезическим координатам.
- •Вычисление плоских прямоугольных координат Гаусса-Крюгера по геодезическим координатам.
- •Местная система плоских прямоугольных координат Гаусса-Крюгера.
Сибирская Государственная Геодезическая Академия
Кафедра высшей геодезии
Курсовая работа
На тему: Системы координат и преобразования между ними.
Выполнил: Проверил:
Ст. гр. ПГ-31 Афонин К. Ф.
Шевченко Г.В.
Новосибирск 2012
Цель работы: Изучить способы преобразования координат в различных системах: референцной и общеземной; геодезической, прямоугольной плоской и пространственной.
Исходные данные:
1) Задание на выполнение курсовой работы.
2) Прямоугольные пространственные координаты точки в системе координат ПЗ-90.02.
Вариант №66
X1=27842.679
Y1=3344066.463
Z1=5414150.223
h1=-22.784
3) Параметры эллипсоидов Красовского и ПЗ-90:
а=6378245м, е2=0.00669342162,
а=6378136.3м, е2=0.00669436619.
4) Элементы ориентирования системы координат СК-42 относительно системы ПЗ-90.02:
x=23.93м, y=-141.03м, z=-79.98м,
ωx=0, ωy=-0.35, ωz=-0.79, Δm=-0.22*10-6.
5) Элементы ориентирования системы координат СК-95 относительно системы ПЗ-90.02:
x1=24.83м, y1=-130.97м, z1=-81.74м,
ω’x=0, ω’y=0, ω’z=-0.13, Δm’=-0.22*10-6.
Системы координат, применяемые в геодезии.
Положение точек на поверхности земного эллипсоида, на поверхности Земли и в пространстве может быть определено с помощью следующих систем координат. В геодезии наибольшее распространение получили следующие системы:
система прямоугольных пространственных координат (X,Y,Z).
система геодезических пространственных координат (B,L,H).
система геоцентрических широт и геодезических долгот (Ф,L).
система плоских прямоугольных координат Гаусса-Крюгера (x,y).
1.1. Система прямоугольных пространственных координат (X,y,z).
За начало координат принимается центр эллипсоида О (рис.1.1.). Ось OZ располагается но полярной оси эллипсоида РОР1, ось ОХ — в плоскости экватора в меридиане РЕР1, который принимается за начальный; ось OY — в плоскости экватора, но в меридиане РКР1: плоскость которого составляет с плоскостью начального меридиана угол в 90°.
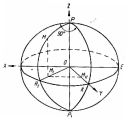
Рис.1.1.
Таким образом, положение точки М поверхности эллипсоида определяется координатами: X=MIMII, Y=OMII, Z=MMI.
Пространственные координаты X, У, Z до последнего времени имели небольшое применение как в теоретических выводах, так и в практических вычислениях. Это объясняется тем, что как сами измерения, так и вычисления производились на поверхности Земли и заключались в вычислении координат ее точек, расстояний между этими точками.
В этом случае наиболее удобной была система координат, непосредственно связанная с поверхностью Земли. Однако в связи с космическими исследованиями возникли геодезические задачи по определению координат точек во внешнем пространстве Земли. При этом система поверхностных координат становится неудобной. Наоборот, система прямоугольных пространственных координат, позволяющая выражать положение точек независимо от поверхности земного эллипсоида, оказывается наиболее целесообразной для решения возникающих задач. Поэтому эта система координат X, Y, Z в настоящее время приобретает большое теоретическое и практическое значение. Метод решения геодезических задач при помощи этой системы координат получил наименование «трехмерной геодезии».
Достоинства системы:
Позволяет однозначно определять положение точки в пространстве.
Для вычисления координат не нужно редуцировать результаты измерений на поверхности эллипсоида. Эту систему удобно применять при математической обработки результатов спутниковых измерений.
Недостатки системы:
Нельзя разорвать тройку координат.
Нельзя уменьшить размерность вектора координат, как в системе геодезических и пространственных координат.
Нет формул прямого перехода к плоским прямоугольным координатам.
