Функциональные связи. Построение уравнения регрессии

Если значение коэффициента свидетельствует о наличии связи, можно переходить к построению модели линейной регрессии, устанавливающей функциональную связь меж­ду признаками.

Определение 15.6. Функциональные связи характеризуются полным соответствием между изменением причины (фак­торного признака х) и изменением результативной ве­личины у, и каждому значению признака-фактора х_i со­ответствует вполне определенное значение результатив­ного признака у_i.

Устанавливая функциональные связи, обычно выполня­ют следующие задачи:

• построение регрессионной модели, т.е. нахождение ана­литического выражения связи;

• прогнозирование по регрессии;

• оценка адекватности модели, ее экономическая интерпре­тация и практическое использование.

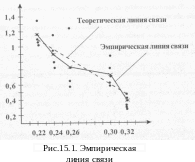
Приблизительное представление о линии связи можно получить на основе эмпирической линии регрессии. Эмпири­ческая линия обычно является ломаной линией, имеет бо­лее или менее значительный излом. Объясняется это тем, что влияние прочих неучтенных причин в средних погаша­ется не полностью в силу недостаточно большого количе­ства наблюдений, поэтому для выбора и обоснования типа кривой эмпирической линией связи можно воспользовать­ся при условии, что число эмпирических данных будет дос­таточно велико.

Одним из элементов конкретных исследований является сопоставление различных уравнений зависимости, основан­ное на использовании критериев качества аппроксимации эмпирических данных конкурирующими вариантами мо­делей. Наиболее часто для характеристики связей экономи­ческих явлений используют следующие типы функций:

• линейную

гиперболическую

• показательную

• параболическую

• степенную

• логарифмическую

Эмпирическая линия регрессии все же больше всего при­ближается к прямой (см. рис. 15.1), и, следовательно, теоре­тическая линия регрессии может быть представлена прямой:

(15.3)

Для нахождения параметров a₀ и а₁ уравнения регрес­сии используется метод наименьших квадратов.

Определение 15.7. Метод наименьших квадратов исполь­зуется для нахождения такой функции, которая наилуч­шим образом соответствует эмпирическим данным, то есть, сумма квадратов отклонений эмпирических точек от теоретической линии регрессии минимальна.

Критерий метода наименьших квадратов можно запи­сать таким образом:

(15.4)

или, поскольку , подставим в правую часть равенства (15.4) и получим:

(15.5)

Применение метода наименьших квадратов для опреде­ления параметров прямой a₀ и a₁ наиболее соответствующей эмпирическим данным, сводится к задаче отыскания экстремума.

Функция двух переменных S(a₀, а₁) может достигнуть экстремума в том случае, когда первые частные производ­ные этой функции равняются нулю,

Вычисляя эти общие производные, получим:

(15.6)

Из уравнений (15.6) получим систему нормальных урав­нений для определения величины параметров а₀ и а_i урав­нения линейной регрессии:

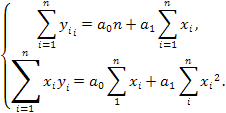(15.7)

Решив систему нормальных уравнений, получаем зна­чения а₀ и а₁, которые подставляются в уравнение линейной регрессии

Определение 15.8. Параметр а₁ в уравнении называют коэффициентом регрессии. При наличии прямой корре­ляционной зависимости коэффициент регрессии имеет по­ложительное значение, а в случае обратной зависимости коэффициент регрессии отрицательный.

Коэффициент регрессии показывает, на сколько в сред­нем изменяется величина результативного признака у при изменении факторного признака х на единицу. Геометрически коэффициент регрессии оценивает степень наклона прямой линии, изображающей уравнение корреляционной зависимости, относительно оси х.

Другому параметру уравнения a₀ не имеет смысла при­давать какое-то определенное толкование, и он, как прави­ло, не имеет независимого значения.

Можно получить значения параметров а₀ и а₁ уравне­ния линейной регрессии более простым способом, зная линейный коэффициент корреляции r.

Для определения коэффициентов линейной регрессии используются следующие формулы:

(15.8)

где r — коэффициент корреляции:

— средние арифметические значений результативного и факторного признаков;

— средние квадратические отклонения значений результативного и факторного признаков.

Наличие соотношения (15.8) дает возможность производить вычисление коэффициента корреляции и параметров уравнения регрессии одновременно.

Коэффициент регрессии применяют для определения коэффициента эластичности.

Определение 15.9. Коэффициент эластичности показывает, на сколько процентов в среднем изменится величина результативного признака у при изменении признака х фактора на один процент.

Для определения коэффициента эластичности используется формула:

(15.9)