
- •Конспекты лекций
- •Содержание
- •1.1. Функция спроса и предложения. Наклон кривой.
- •1.2. Наклон кривой спроса для нормальных товаров.
- •1.3. Наклон кривой предложения для нормальных товаров.
- •Литература
- •Динамические модели рынка одного товара
- •2.1. Паутинообразная модель рынка одного товара Дискретная модель.
- •2.2. Устойчивость равновесия. Сдвиг равновесия.
- •Контрольные вопросы
- •ПроизводствЕнная функция как модель процесса производства
- •3.1. Производственная функция и ее свойства.
- •3.2. Производство с одним переменным фактором.
- •3.3. Замещаемость производственных факторов.
- •3.4. Капиталоемкость технологии.
- •3.5. Эластичность замены одного фактора другим
- •3.6. Два крайних и общий случаи замещения факторов производства.
- •3.7. Изокоста (прямая равных издержек). Правило минимизации издержек фирмы.
- •3.8. Производство с двумя переменными факторами.
- •Контрольные вопросы
- •4.1. Издержки производства в краткосрочном периоде.
- •4.2. Издержки производства в долгосрочном периоде.
- •4.3. Доход фирмы: валовой, средний и предельный.
- •Контрольные вопросы
- •5. Деятельность фирмы на товарных рынках
- •5.1 Равновесие фирмы в условиях совершенной конкуренции.
- •5.2. Рынок чистой монополии. Основные признаки монополии.
- •5.3. Спрос, цена и предельный доход монополиста.
- •5.4. О кривой предложения монополиста.
- •5.5. Необходимое и достаточное условия максимизации
- •5.6. Показатель монопольной власти.
- •5.7. Ущерб, приносимый монополией.
- •5.8. Ценовая дискриминация
- •5.9. Регулирование деятельности монополии с помощью налогов.
3.7. Изокоста (прямая равных издержек). Правило минимизации издержек фирмы.
В
соответствии с производственной функцией
фирма стремится произвести максимальный
объем продукции. Но существуют ограничения:
цены факторов производства:
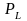 – цена труда,
– цена труда,
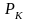 – цена капитала заданы рынком,
– общие издержки фирмы. Фирма расходует
все имеющиеся в ее распоряжении средства
на покупку труда в количестве
– цена капитала заданы рынком,
– общие издержки фирмы. Фирма расходует
все имеющиеся в ее распоряжении средства
на покупку труда в количестве
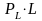 и капитала в количестве
и капитала в количестве
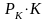 .
Тогда бюджетное ограничение производителя
имеет вид:
.
Тогда бюджетное ограничение производителя
имеет вид:
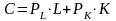 или
или
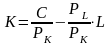 .
Это уравнение изокосты (isocost
line)
(рис. 19а).
Ее наклон отрицателен и равен
.
Это уравнение изокосты (isocost
line)
(рис. 19а).
Ее наклон отрицателен и равен
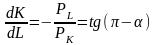 соотношению цен факторов производства.
соотношению цен факторов производства.

Точки на изокосте представляют все возможные сочетания затрат факторов производства, имеющие одинаковую рыночную стоимость.
При перемещении изокосты 2 в положение линии 3 цена капитала растет. На линиях 1 и 2 цены труда и капитала одинаковы.
Фирма
может производить продукцию в точке
в объеме
,
или в точке
в объеме
.
Выпуск
-
максимально возможный. В точке
изокоста касается изокванты. В этой
точке наклон изокосты равен наклону
изокванты. Наклон изокванты измеряется
 ,
а наклон изокосты
,
а наклон изокосты
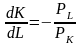 .
Приравняв наклоны изокосты и изокванты,
получим условие минимизации издержек:
.
Приравняв наклоны изокосты и изокванты,
получим условие минимизации издержек:
 или
или
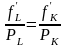 .
В данном случае будут минимальными
средние общие издержки фирмы, так как
при заданном объеме использованных
ресурсов в денежной форме получен
максимально возможный объем выпуска.
.
В данном случае будут минимальными
средние общие издержки фирмы, так как
при заданном объеме использованных
ресурсов в денежной форме получен
максимально возможный объем выпуска.
3.8. Производство с двумя переменными факторами.
Теорию фирмы можно изложить либо с помощью предельных категорий (классический подход), либо с помощью линейного программирования. Эти подходы являются взаимодополняющими.
Используя
предельные категории, рассмотрим
деятельность фирмы в коротком периоде,
когда ее организационная структура
остается стабильной. Производится один
продукт с помощью двух факторов,
производственная функция
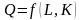 .
В условиях чистой конкуренции фирма
покупает факторы производства по ценам
и
,
и
продает продукт по цене
.
Задача состоит в том, чтобы найти такую
комбинацию
и
,
при которой получают максимум прибыли:
.
В условиях чистой конкуренции фирма
покупает факторы производства по ценам
и
,
и
продает продукт по цене
.
Задача состоит в том, чтобы найти такую
комбинацию
и
,
при которой получают максимум прибыли:

Необходимое
условие максимума прибыли - равенство
первых частных производных нулю:
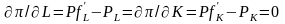 .
Отсюда находим:
.
Отсюда находим:
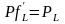 ;
;
 .
(3.3)
.
(3.3)
В
полученных условиях
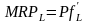 представляет предельный продукт труда,
а
представляет предельный продукт труда,
а
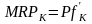 - предельный продукт капитала в денежной
форме. Из условий максимизации прибыли
следует, что фирма увеличивает объем
производства до тех пор, пока предельный
продукт каждого фактора в денежной
форме станет равным цене соответствующего
фактора, т.е. предельным издержкам на
ресурс. Последние равны цене соответствующего
ресурса.
- предельный продукт капитала в денежной
форме. Из условий максимизации прибыли
следует, что фирма увеличивает объем
производства до тех пор, пока предельный
продукт каждого фактора в денежной
форме станет равным цене соответствующего
фактора, т.е. предельным издержкам на
ресурс. Последние равны цене соответствующего
ресурса.
Из
уравнений (3.3) определяем расходуемые
количества
и
как
функции цен
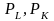 и
.
Запишем необходимое условие максимума
прибыли в виде:
и
.
Запишем необходимое условие максимума
прибыли в виде:
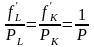 или
или
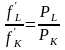 .
.
Оно означает, что для достижения максимума прибыли необходимо, чтобы предельная норма технологического замещения факторов MRTS была равна заданному соотношению их цен.
Достаточное
условие максимизации прибыли заключается
в том, что для любого отклонения, при
котором
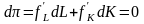 (или
(или
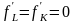 )
дифференциал второго порядка
)
дифференциал второго порядка
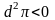 .
.
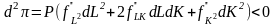 .
(3.4)
.
(3.4)
Положение
фирмы, характеризуемое уравнениями
(3.3) и (3.4), достигается в два этапа.
Во-первых, если наряду с ценами
и
задан объем выпуска
,
которые представляют собой ограничения
в деятельности фирмы, тогда величины
затрачиваемых факторов
и
определяются
таким
образом, чтобы минимизировать издержки
производства
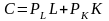 при условии
.
при условии
.
Решение
может быть таким. Из
выразим
как
функцию
и заданного
.
Тогда
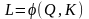 .
Подставляем
в функцию издержек
,
и она становится функцией от одной
переменной
,
т.е.
.
Подставляем
в функцию издержек
,
и она становится функцией от одной
переменной
,
т.е.
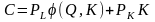 .
Приравниваем к нулю первую производную
.
Приравниваем к нулю первую производную
 и находим K.
Убедимся, что найденное
действительно является минимальной
величиной затрат капитала. Зная
,
из
находим
.
Но этот метод не всегда применим. Не
всегда бывает легко с помощью
производственной функции выразить одну
переменную через другую, например
через
.
В таких случаях пользуются методом
множителей Лагранжа.
и находим K.
Убедимся, что найденное
действительно является минимальной
величиной затрат капитала. Зная
,
из
находим
.
Но этот метод не всегда применим. Не
всегда бывает легко с помощью
производственной функции выразить одну
переменную через другую, например
через
.
В таких случаях пользуются методом
множителей Лагранжа.
Запишем условия максимизации прибыли, если продукт реализуется на рынке несовершенной конкуренции. Заданы функции предложения ресурсов и спроса на продукцию фирмы.
Функция
спроса имеет однородную форму
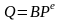 ,
где
,
где
 ,
-
цена продукта,
-
ценовая эластичность спроса. Если
,
-
цена продукта,
-
ценовая эластичность спроса. Если
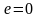 ,
то цена продукта становится постоянной
величиной и имеем условия совершенной
конкуренции. Обратная функция спроса
,
то цена продукта становится постоянной
величиной и имеем условия совершенной
конкуренции. Обратная функция спроса
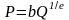 ,
где
,
где
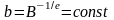 .
Валовой доход фирмы
.
Валовой доход фирмы
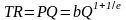 .
Если
.
Если
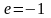 ,
то валовой доход является постоянным,
не зависящим от
и
.
Это значит, что объем производства
является заранее заданной величиной
,
то валовой доход является постоянным,
не зависящим от
и
.
Это значит, что объем производства
является заранее заданной величиной
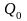 ,
а, следовательно, и цена
в выражении (
)
также постоянна.
,
а, следовательно, и цена
в выражении (
)
также постоянна.
Функции
предложения труда
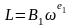 ,
капитала
,
капитала
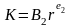 также
однородны,
также
однородны,
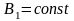 и
и
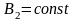 ,
,
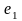 и
и
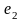 - эластичности предложения факторов
производства,
- эластичности предложения факторов
производства,
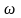 и
и
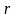 ,
соответственно, ставка заработной платы
и процент на единицу капитала.
,
соответственно, ставка заработной платы
и процент на единицу капитала.
Определим
и
,
соответствующие предложению труда и
капитала при названных условиях. Тогда
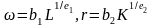 ,
где
,
где
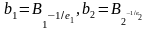 .
Затраты труда и капитала равны:
.
Затраты труда и капитала равны:
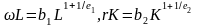 .
.
Запишем функцию Лагранжа для экономической прибыли:
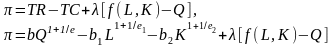 ,
где
- множитель Лагранжа.
,
где
- множитель Лагранжа.
Необходимые условия максимизации прибыли:

Последнее уравнение добавляется, если является переменной величиной. Из системы уравнений находим:
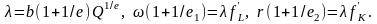
Если
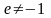 ,
то
,
то
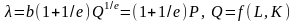
Если
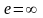 ,
то
,
то
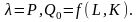
Определим факторные цены в условиях несовершенной конкуренции:
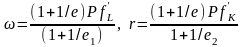
Полученные выражения отражают характер зависимости заработной платы и ставки процента от рыночных параметров – цены товара, ценовой эластичности спроса на товар, ценовой эластичности предложения труда и капитала, а также предельной производительности труда и капитала. Решая систему уравнений, представляющую необходимое условие максимизации прибыли, находим значения , , и .
Достаточное
условие максимизации прибыли
 <0.
Если оно выполняется при найденных
значениях
,
,
и
,
то фирма получает максимальную прибыль.
<0.
Если оно выполняется при найденных
значениях
,
,
и
,
то фирма получает максимальную прибыль.
Задания для практических занятий
1.
Определить отдачу от масштаба для
следующих производственных функций:
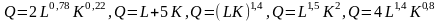 .
.
2.
Выпуск продукта задается формулой
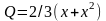 ,
где
- количество единственного используемого
ресурса. Определить предельный продукт
ресурса для
,
где
- количество единственного используемого
ресурса. Определить предельный продукт
ресурса для
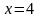 .
.
3.
Дана производственная функция
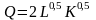 .
Найти предельный продукт труда
(предельную производительность труда
),
предельный продукт капитала
.
Найти предельный продукт труда
(предельную производительность труда
),
предельный продукт капитала
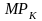 (предельную производительность капитала
)
при
(предельную производительность капитала
)
при
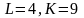 .
Определите предельную норму замещения
капитала трудом (
)
при расходе ресурсов
.
Определите предельную норму замещения
капитала трудом (
)
при расходе ресурсов
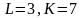 .
.
4. Какого типа производственная функция характеризует производственный процесс, в котором эластичность замещения факторов производства неизменна?
Определить эластичность замены одного фактора производства другим для производственных функций:
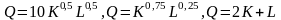 .
.Технология производства продукта в 2000 году воплощалась в производственной функции
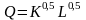 ,
в 2001 году – в функции
,
в 2001 году – в функции
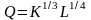 .
Как следует охарактеризовать технический
прогресс в таком случае? При
.
Как следует охарактеризовать технический
прогресс в таком случае? При
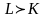 и
и
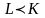 ?
При
?
При
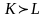 и
?
и
?Траектория увеличения выпуска стала более крутой. Причиной этого может быть
технический прогресс, расходующий капитал и экономящий труд;
повышение цены капитала, так как потребление капитала увеличивается;
повышение цены труда, так как труд замещается капиталом.
Если в результате технологических нововведений выпуск при неизменном количестве ресурсов возрастает,
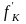 и
снижаются, причем
снижается быстрее, чем
,
то
и
снижаются, причем
снижается быстрее, чем
,
то
- нововведения технически неэффективны;
средний продукт труда снижается;
средний продукт капитала снижается;
имеет место капиталоинтенсивный технический прогресс. Какое утверждение верно?
Компания использует только эффективные способы производства. Недавно она внесла изменения в процесс производства, в результате которых
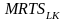 увеличилась, хотя выпуск не изменился.
Это означает, что капиталоемкость
производства понизилась, возросла, не
изменилась; могла снизиться, могла
возрасти, но изменилась; капиталоемкость
продукции
увеличилась, хотя выпуск не изменился.
Это означает, что капиталоемкость
производства понизилась, возросла, не
изменилась; могла снизиться, могла
возрасти, но изменилась; капиталоемкость
продукции
 понизилась. Найдите верный ответ.
понизилась. Найдите верный ответ.
10. Наборы ресурсов (11,6), (8,8) имеют стоимость 40 руб. каждый. Определить цены труда , капитала и наклон изокосты.
11.
Дано: производственная функция фирмы
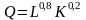 ,
издержки составляют
,
издержки составляют
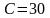 руб.,
цена труда
руб.,
цена труда
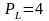 руб.,
цена капитала
руб.,
цена капитала
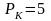 руб. Найти равновесный набор ресурсов,
при котором издержки фирмы на единицу
продукции минимальны.
руб. Найти равновесный набор ресурсов,
при котором издержки фирмы на единицу
продукции минимальны.
12.
Производственная функция фирмы
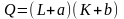 .
Цена труда
.
Цена труда
 ,
цена капитала
,
цена капитала
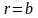 ,
цена продукта
,
цена продукта
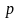 .
Определить значения
и
,
при которых прибыль фирмы максимальна.
.
Определить значения
и
,
при которых прибыль фирмы максимальна.
