10.5 Кинетика коагуляции.

Скорость коагуляции является основным фактором, по которому судят об агрегативной устойчивости, может изменяться в широких пределах.

Количественная теория была развита в трудах М. Смолуховского, Г. Мюллера, Н. Фукса. Наиболее разработанной и одной из первых была теория Смолуховского:

- для монодисперсных золей со сферическими частицами

- столкновение частиц – результат броуновского движения

- критическое расстояние при взаимодействии d=2r

- столкновение только 2 частиц (одинарная с одинарной, одинарная с двойной, двойная с тройной).

Такое представление позволило свести коагуляцию к теории бимолекулярной хим. реакции. В результате скорость коагуляции может быть найдена:

;

P – стерический фактор

- суммарное число r

Д – коэффициент диффузии

После интегрирования в пределах от при τ=0 до ν_τ при τ:

к – определить трудно, поэтому Смолуховским было введено понятие времени половинной коагуляции – времени, в течении которого число частиц уменьшается в 2 раза ( ).

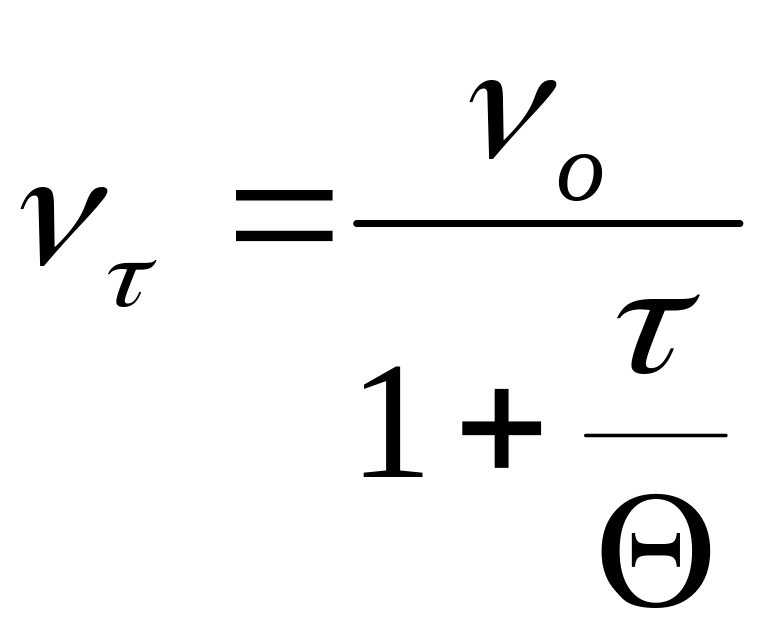
Приравняв эти уравнения, получим:

, ;

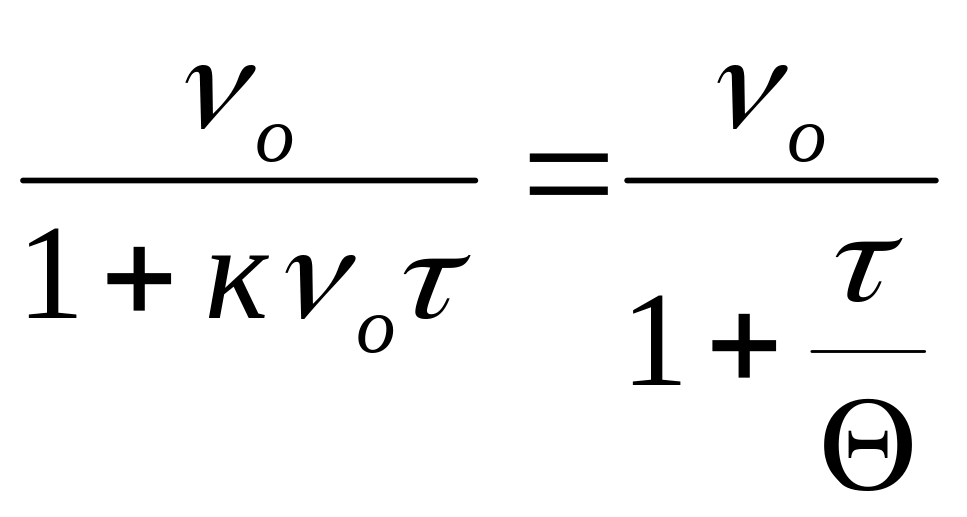Решение кинетических уравнений коагуляции можно проводить графически:

; .

Согласно теории кинетики коагуляции, различают быструю и медленную коагуляцию. При быстрой коагуляции все столкновения частиц заканчиваются их слипанием. Такому положению отвечает условие: и Р=1. Тогда

; ; , то

, а , т.е.

при быстрой коагуляции К зависит только от η и Т. Экспериментально доказано Зигмонди. При медленной коагуляции , Р≠1 (необходимо учитывать эффективность соударений). Фуксом был введен коэффициент замедления.

10.6 Коагуляция золей электролитами

Т.к. одним из основных факторов устойчивости золей (гидрофобных) является электростатический, то введение в систему электролита может привести к сжатию ДЭС и усилению притяжения частиц. Наименьшая концентрация электролита «с_м» при которой начинается коагуляция (медленная), называется порогом коагуляции. Быстрая коагуляция начинается при , когда скорость остается const. С_м – сильно зависит от метода его определения, от концентрации золя и т.д. Коагулирующее действие электролита сильно зависит от Z противоионов. По ДЛФО соотношение С_м для зарядов .

Экспериментально было установлено:

1. (порог коагуляции)

2. коагулирующей способностью обладают лишь те электролиты, знак заряда ионов которых противоположен заряду коллоидных частиц и тем сильнее, чем больше Z

3. для неорганических ионов одинаковой валентности коагулирующая активность увеличивается с уменьшением степени их гидратации.

Ряды Тофмейстера:

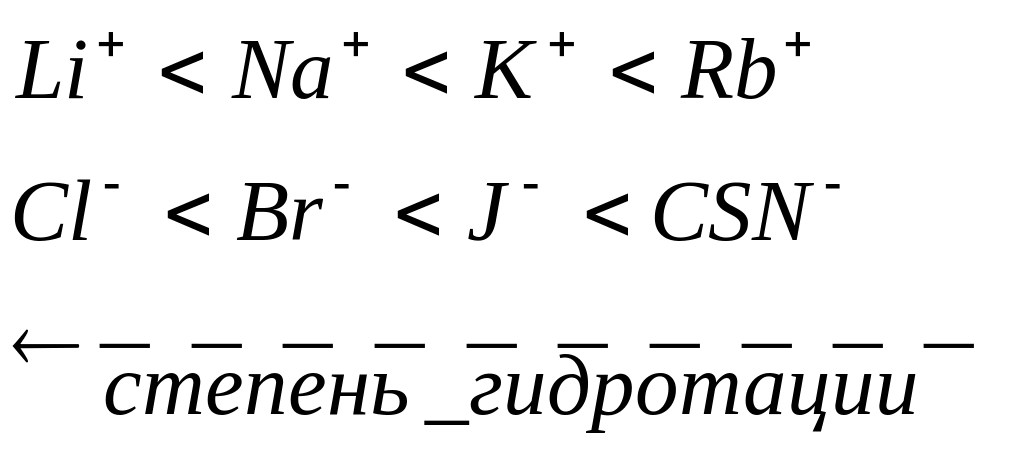
4. коагулирующее действие смеси электролитов часто бывает неаддитивным (либо хуже, либо значительно лучше)

5. более сильное влияние электролитов, вступающих в химическую реакцию с противоионами.

10.7 Условие термодинамической устойчивости дисперсных систем

1. т.к. равновесное состояние системы отвечает min G. Изменение энергии Гиббса при образовании таких систем должно быть <0, ∆G<0.

2. ультрамикрогетерогенность. Только в таких системах избыточная поверхностная энергия может компенсироваться составляющей в связи с возможностью теплового движения (броуновского) частиц. Максом Фольмером (нем.) это было доказано экспериментально 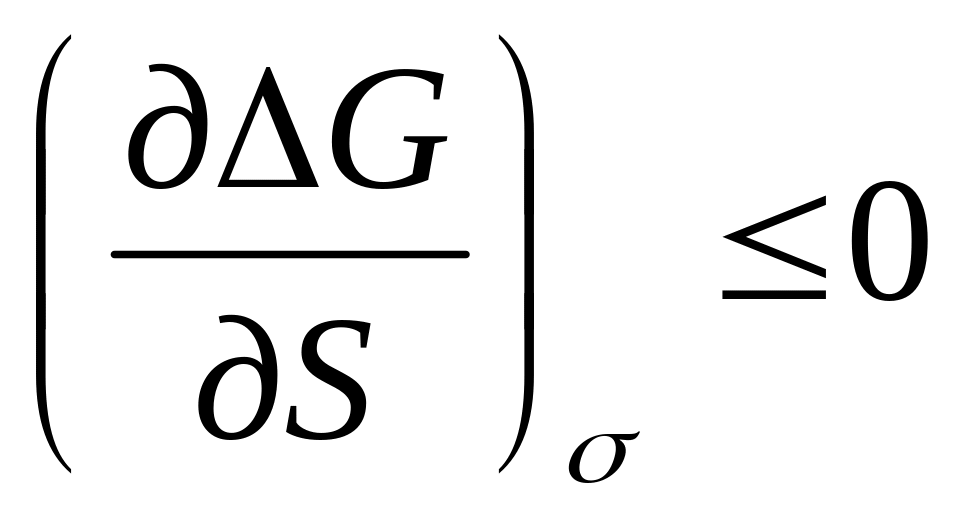; , т.е. энергия Гиббса не должна увеличиваться с увеличением межфазной поверхности или с уменьшением размера частиц.

3. необходимость жидкой дисперсной среды, т.к. малое значение σ возможно только при значительном межфазном взаимодействии, что характерно для жидкой среды.

4. стремление системы к самодиспергированию, т.к. самопроизвольный рост межфазной поверхности может иметь место при компенсировании σ, при увеличении энтропии системы (что возможно в жидких средах из-за малых σ).

5. соответствие мах возможных значений σ уравнению Ребиндера-Щукина. 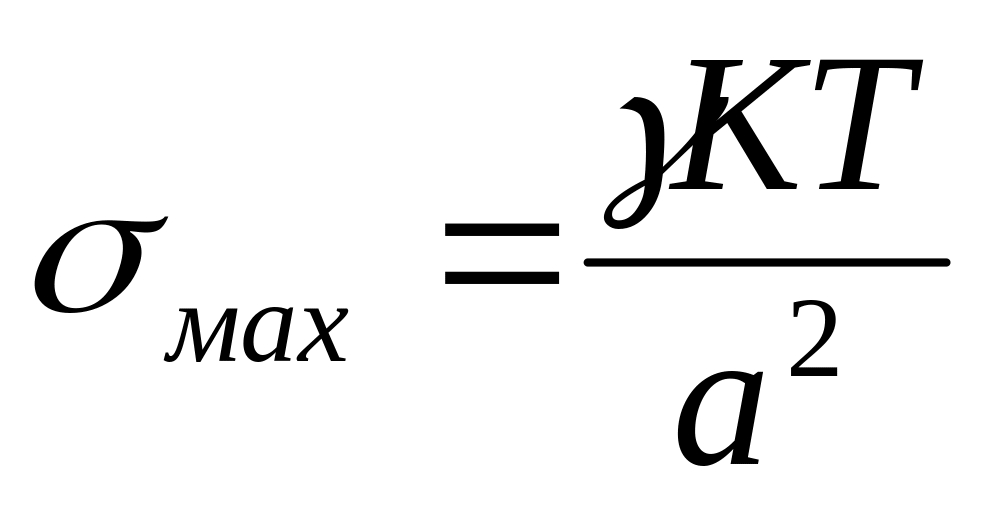, К – коэффициент, а – средний размер частиц.

6. равенство скоростей двух противоположных процессов – коагуляции и пептизации .
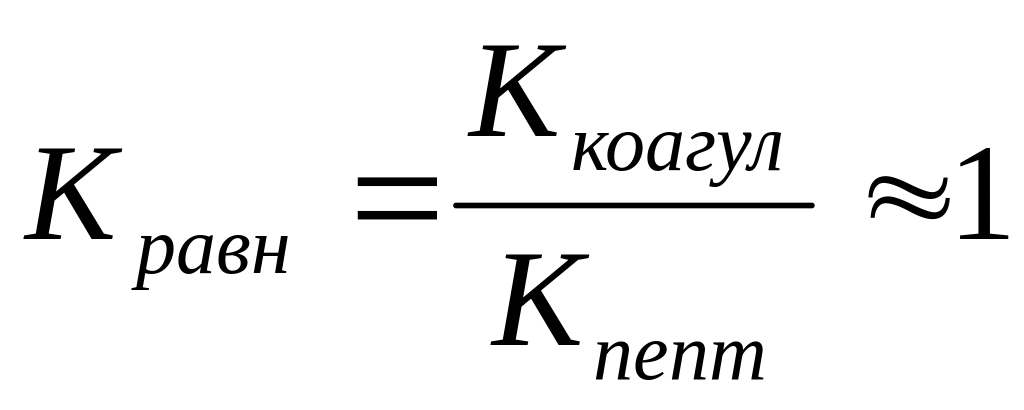