Лабораторная работа № 6 Устойчивость разомкнутых и замкнутых систем
Цель работы
1. Ознакомление со свойствами частотных характеристик разомкнутых систем автоматического управления, исследование устойчивости линейных систем по их частотным характеристикам;
2. Ознакомление с методиками построения корневых годографов и получение навыков оценки переходных характеристик замкнутых систем по расположению корней характеристического уравнения;
3. Получение навыков определения качественных показателей временных характеристик замкнутых систем по частотным характеристикам разомкнутых систем.
Теоретическое обоснование
Если передаточная функция разомкнутой системы известна
, (6.1)
то полюсами замкнутого контура являются корни уравнения
KB(s) + A(s) = 0.
Качество переходных процессов зависит от расположения корней характеристического уравнения замкнутой системы. Чем дальше корень (полюс) расположен от мнимой оси, тем меньше время переходного процесса. Колебательная составляющая определяется отношением мнимой части корня к действительной части, и чем больше это отношение, тем больше колебательная составляющая.
Корневым годографом характеристического уравнения по вещественному параметру называют совокупность траекторий, которые прочерчивают на комплексной плоскости корни этого уравнения при изменении параметра от нуля до бесконечности. Корневой годограф обладает свойствами.
1. Корневой годограф уравнения (6.1) имеет несколько траекторий.
2. Траектории корневого годографа симметричны относительно действительной оси, так как уравнение (6.1) имеет действительные коэффициенты и, следовательно, его комплексные корни должны быть сопряжёнными парами.
3. Каждый корень уравнения si является, в общем случае, неявной функцией от параметра . Траектория, которую прочерчивает этот корень на комплексной плоскости при изменении частоты от нуля до бесконечности, является параметрическим графиком функции si().
4. Началом траектории называют точку, в которой находится корень при = 0. Следовательно, все i траекторий корневого годографа начинаются в начальных точках si(=0).
5. Направление траектории определяют по направлению перемещения корня при увеличении и обычно указывают стрелкой.
6. Концом траектории называют точку, к которой стремится корень при ∞.
7. Траектория корней не может иметь точек самопересечения.
При передвижении по кривой годографа можно определить значения корней, коэффициента демпфирования и величины перерегулирования замкнутой системы. Если на кривой корневого годографа выбрать определенную точку, то в этой точке будет получен соответствующий коэффициент усиления разомкнутой системы, который будет определять временные характеристики замкнутой системы.
В Matlab существует возможность построения корневого годографа и выбора коэффициента усиления разомкнутой системы, определяющего заданные качества переходного процесса, по передаточным функциям одноконтурных разомкнутых систем. Команда rlocus(h) строит корневой годограф замкнутой системы по модели разомкнутой системы.
Качество переходных процессов можно определить с помощью запасов устойчивости по амплитуде и фазе.
Запас устойчивости по амплитуде – это величина модуля логарифмической амплитудно-частотной характеристики разомкнутой системы на частоте, при которой фазовая частотная характеристика имеет значение –180.
Запас устойчивости по фазе – это разность между значением фазовой частотной характеристики и значением –180 по частоте среза. Частота среза – это частота, при которой значение амплитудно-частотной характеристики равно 1.0 или 0 дБ.
Определение устойчивости линейной системы также производят с помощью критерия Найквиста.
Для этого на комплексной плоскости строят АФХ разомкнутой системы, полученную теоретическим или экспериментальным путем, по виду которой с помощью критерия Найквиста определяют поведение исследуемой системы в замкнутом состоянии. Если АФХ разомкнутой системы не охватывает точку с координатами (–1, ј0), то замкнутая система, полученная из разомкнутой устойчивой системы, будет устойчива. Если АФХ разомкнутой системы охватывает точку с координатами (–1, ј0), то замкнутая система, полученная из разомкнутой устойчивой системы, будет неустойчива. Если АФХ разомкнутой системы проходит через точку (–1, ј0), то замкнутая система, полученная из разомкнутой устойчивой системы, будет находиться на границе устойчивости.
Все положения критерия Найквиста сформулированы также и относительно ЛАЧХ и ЛФЧХ, разомкнутой системы. Если ЛАЧХ разомкнутой системы пересекает линии 0 дБ раньше, чем ЛФЧХ пересекает линию –180°, то замкнутая система будет устойчивой. Если ЛАЧХ разомкнутой системы пересекает линию 0 дБ позже, чем ЛФЧХ пересекает линию –180°, то замкнутая система будет неустойчивой. Если ЛАЧХ разомкнутой системы пересекает линию 0 дБ на частоте, при которой ЛФЧХ пересекает линию –180°, то система находится на границе устойчивости. Это означает, что на частоте ω система регулирования не изменяет по амплитуде входной сигнал, а вносит фазовое запаздывание равное –180°.
Команда margin определяет запасы устойчивости по амплитуде и фазе.
Описание работы
Для заданной передаточной функции построение корневого годографа (рис. 6.1) выполняется с помощью команд:
h=tf([1,0.5,1],[1,0.4,2,0]); %Передаточная функция системы
rlocus(h) %Построение корневого годографа.
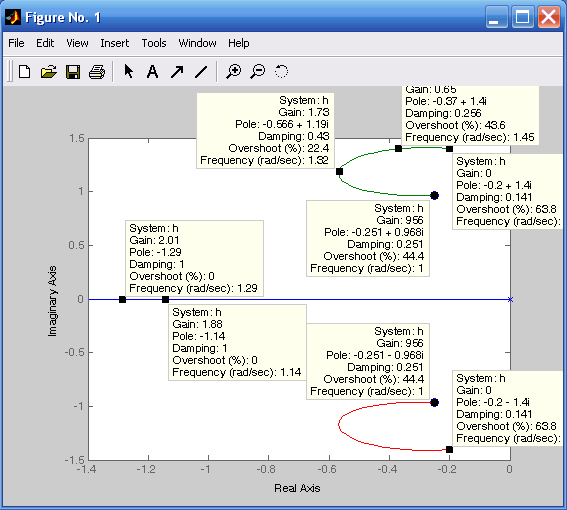
Рис.6.1. Корневой годограф с динамическими параметрами системы в выбранной точке
При щелчке по кривой корневого годографа кнопкой мыши выбирается точка корневого годографа (рис. 6.1). Каждая точка характеризуется коэффициентом усиления разомкнутой системы (Gain), значением полюсов замкнутой системы (pole), коэффициентом демпфирования замкнутой кривой системы (Damping), величиной перерегулирования в % (overshot), частотой среза системы (Frequency).
Для определения запасов по амплитуде и фазе выбраны коэффициенты k: 100; 10; 1; 0,1, для которых определены запасы по фазе и амплитуде, а затем построены переходные характеристики
k1=100;h1=k1*h; %Передаточная функция разомкнутой системы при k1=100
k2=10;h2=k2*h; %Передаточная функция разомкнутой системы при k2=10
k3=1;h3=k3*h; %Передаточная функция разомкнутой системы при k3=1
k4=0.1;h4=k4*h; %Передаточная функция разомкнутой системы при k4=0.1
figure(2),bode(h1,h2,h3,h4),grid %ЛАЧХ, ЛФЧХ систем
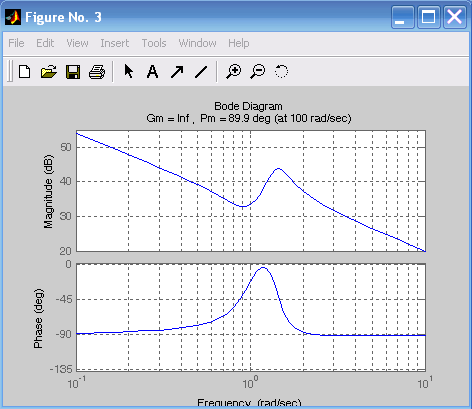
figure(3),margin(h1),grid %Определение запаса по фазе
figure(4), margin(h2),grid %и амплитуде для h1, h2, h3, h4
figure(5),margin(h3),grid
figure(6),margin(h4),grid
h10=feedback(h1,1) %Определение передаточных
h20=feedback(h2,1) %функций замкнутых систем
h30=feedback(h3,1)
h40=feedback(h4,1)
figure(7) %Переходные характеристики замкнутых систем
step(h10,h20,h30,h40,10),grid.
Так как передаточные функции h1, h2, h3 и h4 отличаются только коэффициентом усиления, то логарифмическая фазовая частотная характеристика будет у них общая (рис. 6.2). Переходные характеристики, иллюстрирующие динамику поведения системы, показаны на рис. 6.3.
Команда margin определяет запасы устойчивости по амплитуде и фазе, а команда step строит переходные характеристики.
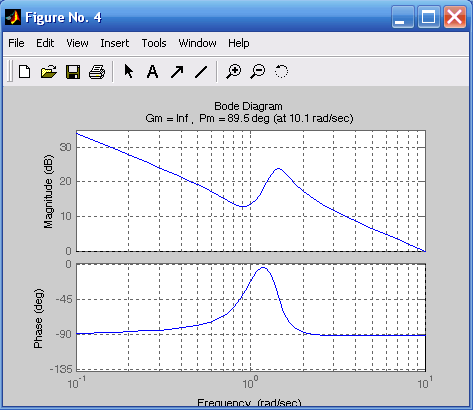
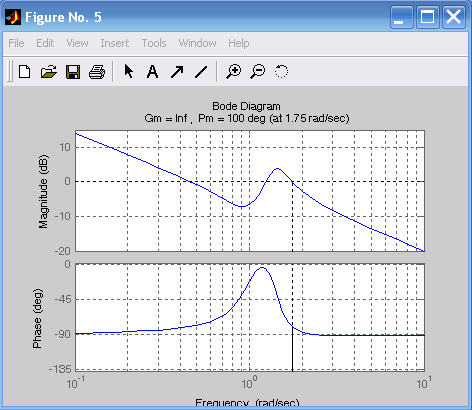
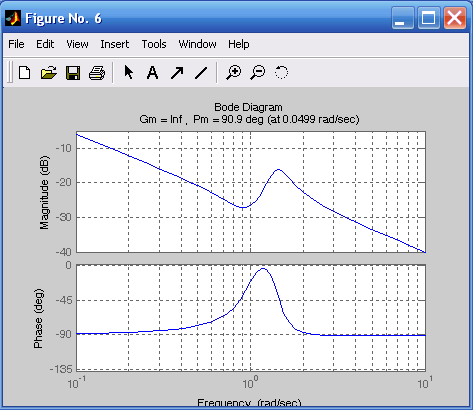
На рис. 6.4 приведены ЛАЧХ и ЛФЧХ исследуемой системы и указаны запасы по амплитуде и по фазе. При этом для k1 = 100 (рис. 6.4а) запас устойчивости по фазе составляет 89,6 на частоте 100с–1, для k2 = 10 (рис. 6.4б) запас устойчивости по фазе составляет 89,6 на частоте 10,1с–1, для k3 = 1 (рис. 6.4в) запас устойчивости по фазе составляет 100 на частоте 1,75с–1, для k4 = 0,1 (рис. 6.4г) запас устойчивости по фазе составляет 90,9 на частоте 0,050с–1. Так как ЛФЧХ не пересекает значение = –180, то запас по амплитуде не определяют.
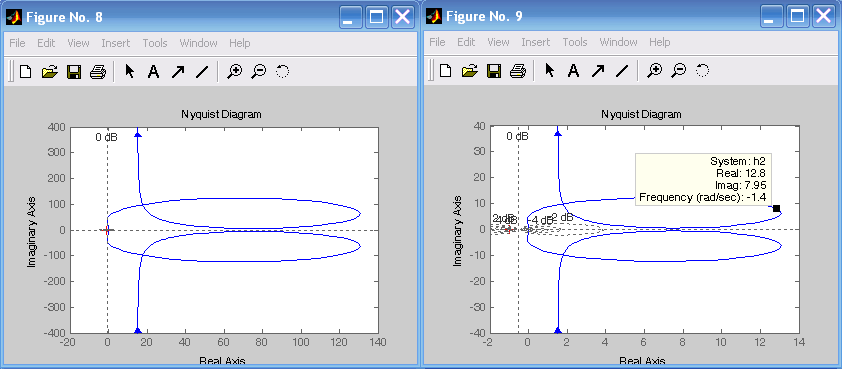
Для рассмотрения устойчивости системы по критерию Найквиста строят АФХ. Так как АФХ разомкнутых систем не охватывает точку (–1, j0), то системы устойчивы в замкнутом состоянии (рис. 6.5).
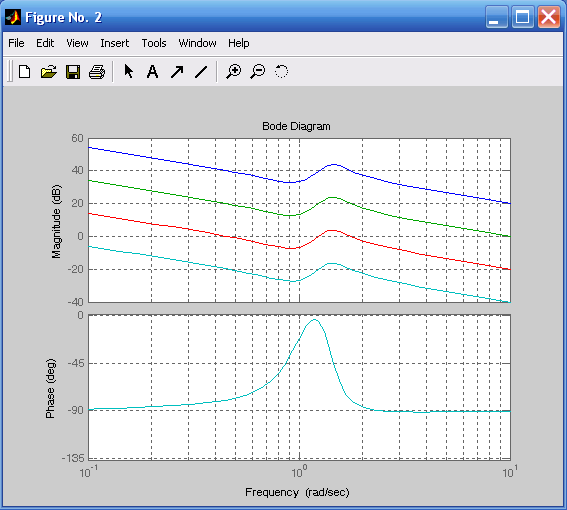
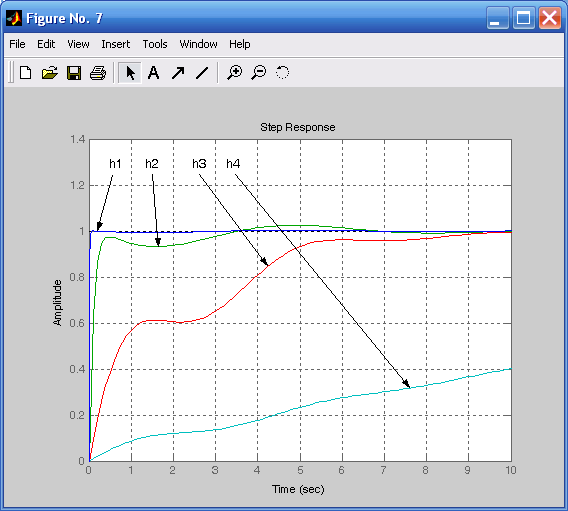
Рис. 6.2. ЛАЧХ и ЛФЧХ Рис. 6.3. Переходные характеристики
а) б)
в) г)
Рис. 6.4. ЛАЧХ и ЛФЧХ, соответствующие передаточным функциям h1, h2, h3, h4
а) б)
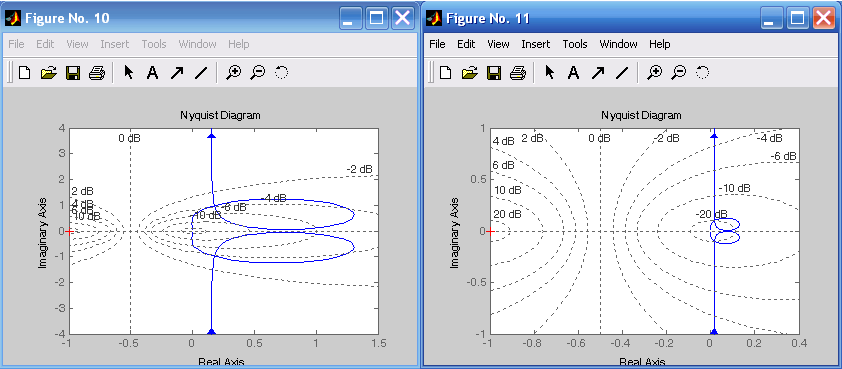
в) г)
Рис. 6.5. АФХ, соответствующие передаточным функциям h1, h2, h3, h4
figure(8), nyquist(h1),grid
figure(9), nyquist(h2),grid
figure(10), nyquist(h3),grid
figure(11), nyquist(h4),grid.
Приведенные характеристики позволяют установить связь между ЛАЧХ и качеством переходного процесса: при значительном запасе по фазе и значительной частоте среза системы переходной процесс характеризуется большим быстродействием и малым перерегулированием (кривая h1). При уменьшении частоты среза системы перерегулирование возрастает, а быстродействие падает (кривые h1, h2, h3, h4). Анализируя ЛАЧХ, ЛФЧХ и АФХ разомкнутой системы можно оценить качество переходных процессов замкнутых систем.
Задание
1. Для заданной передаточной функции построить корневой годограф, по корневому годографу (рис. 6.1) определить изменение динамических параметров системы при изменении частоты .
2. Определить критические значения коэффициентов усиления передаточной функции.
3. Построить логарифмические частотные характеристики системы при коэффициентах усиления k = 100, 10, 1, 0,1 (рис. 6.2).
4. Построить переходные характеристики (рис. 6.3)
5. Определить запасы устойчивости по амплитуде и фазе (рис. 6.4).
6. Построить амплитудно-фазные характеристики (рис. 6.5).
7. Используя критерий Найквиста составить прогноз на поведение системы в замкнутом состоянии. Если АФХ разомкнутой системы охватывает точку (–1, j0), то изменением параметров добиться устойчивости системы в замкнутом состоянии.
8. Определить частоту среза ωc1 и фазовый сдвиг 1 для устойчивой системы h1.
9. Изменением параметров звена h1 добиться того, чтобы АФХ разомкнутой системы охватывала точку с координатами (–1, j0), что соответствует неустойчивой системе в замкнутом состоянии.
10. Определить частоту среза ωc2 и фазовый сдвиг 2 для неустойчивой системы.
11. В пакете Simulink собрать модель разомкнутой системы с параметрами, соответствующими устойчивой системе. На вход подать гармонические колебания с частотой ωc1 и определить комплексный коэффициент передачи.
12. Сравнить данные пакета Simulink и пакета Control Toolbox и сделать выводы.
13. В пакете Simulink собрать модель разомкнутой системы с параметрами, соответствующими неустойчивой системе. На вход подать гармонические колебания с частотой ωc2 и определить комплексный коэффициент передачи.
Содержание отчета
1. Результаты построений по пунктам заданий 1 – 13.
2. Выводы по результатам построений.
Контрольные вопросы
1. По каким уравнениям строится корневой годограф и как его можно использовать при оценке качества переходного процесса.
2. Дайте определение запаса устойчивости по амплитуде и фазе.
3. Как будут располагаться логарифмические характеристики системы, находящейся на грани устойчивости.
4. По какой команде определяется запас по фазе и амплитуде.
5. Найдите передаточную функцию замкнутой системы.
6. Какой командой определяется замкнутая система с положительной и отрицательной обратной связью.
7. Как формируется критерий Найквиста по АФХ разомкнутой системы?
8. Как формируется критерий Найквиста по логарифмическим характеристикам разомкнутой системы?
9. Как определить АФХ экспериментальным путем?
10. Как определить фазовый сдвиг экспериментальным путем?
11. Как определить запас по фазе и амплитуде?
12. Чем отличаются АФХ статической и астатической систем?
13. Какие условия нахождения системы на границе устойчивости?
14. В чем отличие графиков логарифмических характеристик статических и астатических систем?