
- •Лабораторная работа № 1 Исследование типовых динамических звеньев
- •Impulse(h1,h2,h3),grid %Весовые функции
- •Лабораторная работа №2 Определение коэффициентов дифференциальных уравнений и частотных характеристик в Simulink
- •Лабораторная работа № 3 Решение дифференциальных уравнений в пакете Simulink
- •Лабораторная работа № 4 Моделирование систем автоматического управления методом вариации постоянных
- •Лабораторная работа № 5 Представление линейных моделей систем регулирования в пакетах Matlab и Simulink
- •Лабораторная работа № 6 Устойчивость разомкнутых и замкнутых систем
- •Лабораторная работа № 7 Исследование связей между законами регулирования и требованиями к качеству регулирования
- •Лабораторная работа № 8 Исследование систем регулирования в siso Design Tool
- •Лабораторная работа № 9 Исследование системы регулирования с корректирующими звеньями
- •Лабораторная работа № 10 Синтез систем автоматического управления по заданному расположению корней
- •Лабораторная работа № 11 Способы представления дискретных систем автоматического управления
- •Лабораторная работа № 12 Определение амплитудно-фазовых характеристик дискретных систем
- •Лабораторная работа № 13 Исследование устойчивости дискретных систем на плоскостях p, z и w
- •Vpa(hh); %Точность вычисления функции
- •Лабораторная работа № 14 Исследование дискретных систем регулирования
- •Лабораторная работа № 15 Определение структурных схем дискретных систем по уравнениям пространства состояния аналогового эквивалента
- •Лабораторная работа № 16 Определение параметров цифрового регулятора линейных и нелинейных систем методом пространства состояний
- •Описание работы Определение фундаментальной матрицы линейной системы (рис. 16.1) проводится по алгоритму
- •Откуда получаем
Лабораторная работа № 4 Моделирование систем автоматического управления методом вариации постоянных
Цель работы
1. Аналитическое вычисление фундаментальных матриц при моделировании системы методами прямого, параллельного и последовательного программирования.
2. Решение дифференциальных уравнений методом вариации постоянных.
Теоретическое обоснование
Лабораторная работа выполняется на основе моделей и индивидуального задания лабораторной работы №3.
Непрерывная линейная система также может быть описана дифференциальным векторно-матричным уравнением
(4.1)
где А – матрица коэффициентов состояний размером kk; В – матрица коэффициентов управления размером kn; С – матрица коэффициентов наблюдения размером mk и D – матрица коэффициентов выхода размером mn; X – вектор состояния (матрица-столбец размером kl); U – вектор управления (матрица-столбец размером nl); Y – вектор наблюдения (матрица-столбец размером ml).
Решение уравнения (4.1) можно выразить через фундаментальные матрицы, определенные несколькими методами.
Первый метод основан на взятии конечного числа элементов разложения
![]() ,
,
где
![]()
Второй способ основан на аналитическом вычислении матрицы Ф(t).
Преобразование
Лапласа векторного дифференциального
уравнения
![]() дает sX(s)
− X(0)
=
AX(s).
Откуда
X(s)
[Is
−
A]
= X(0)
или
X(s)
= [Is
–
A]-1X(0),
где
I
– единичная
матрица.
дает sX(s)
− X(0)
=
AX(s).
Откуда
X(s)
[Is
−
A]
= X(0)
или
X(s)
= [Is
–
A]-1X(0),
где
I
– единичная
матрица.
При применении к обеим частям последнего уравнения обратного преобразования Лапласа X(t) = L-1{[Is − A]-1}X(0).
Выражение L-1{[Is − A]-1} = eAt = Ф(t) определяет фундаментальную матрицу системы.
Множество решений
однородного векторно-матричного
дифференциального уравнения
![]() где каждому начальному условию
где каждому начальному условию
![]() соответствует только одно решение
дифференциального уравнения, образует
N-мерное
векторное пространство. Среди множества
решений всегда может быть выбрано n
линейно независимых. Матрица X(t)[nn],
столбцами которой являются n
линейно
независимых решений системы, называется
фундаментальной матрицей этой системы
дифференциальных уравнений.
соответствует только одно решение
дифференциального уравнения, образует
N-мерное
векторное пространство. Среди множества
решений всегда может быть выбрано n
линейно независимых. Матрица X(t)[nn],
столбцами которой являются n
линейно
независимых решений системы, называется
фундаментальной матрицей этой системы
дифференциальных уравнений.
Общее решение матричного дифференциального уравнения для известной фундаментальной матрицы Ф(t) определяется формулой Коши (формулой вариации постоянных)
![]() (4.2)
(4.2)
где – собственные значения матрицы Ф.
Описание работы
Рассмотрим систему с передаточной функцией (4.3)
![]() (4.3)
(4.3)
Метод прямого программирования
Рис. 4.1. Схема моделирования системы методом прямого программирования
 (4.4)
(4.4)
 C
= [3 4 1], D
= 0.
C
= [3 4 1], D
= 0.
Аналитическое вычисление фундаментальной матрицы заключается в определении матрицы состояния A, разности [Is − A], нахождении обратной матрицы и применении обратного преобразования Лапласа к каждому элементу обратной матрицы.
В пакете MatLab эти операции выполняются следующим образом.
A=[0,1,0;0,0,1;0,-10,-7] %Матрица состояния А
syms s %Символьная переменная
Is=[s,0,0;0,s,0;0,0,s] %Единичная матрица
F=inv([Is]-[A]) %Обратная матрица в частотной области
F1=ilaplace(F) %Обратная матрица во временной области.
В результате выполнения программы получают фундаментальную матрицу в частотной области
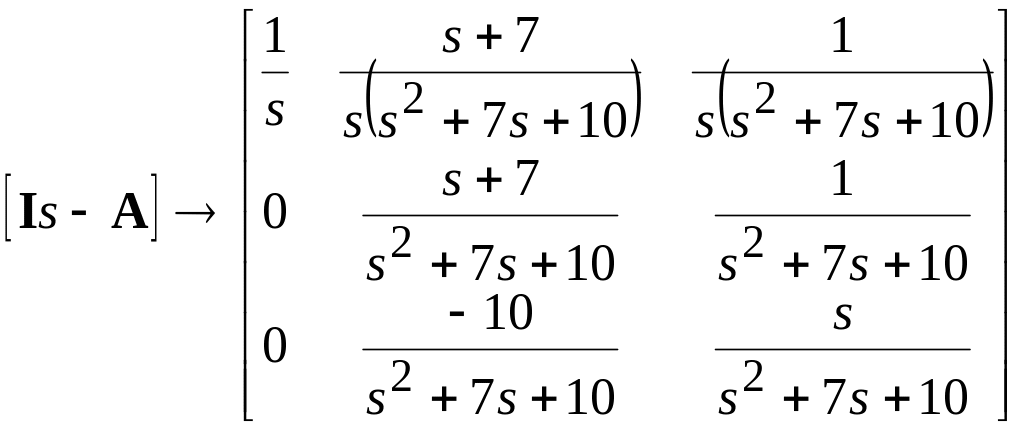 (4.5)
(4.5)
и во временной области
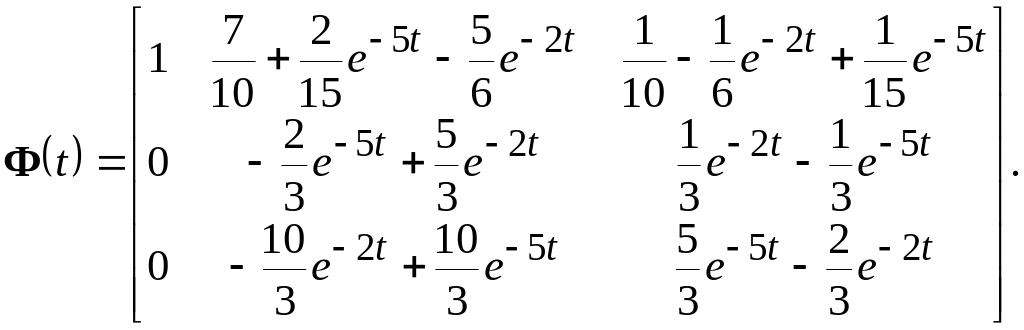 (4.6)
(4.6)
Выражение (4.6) получено из (4.5) с помощью обратного преобразования Лапласа применительно к каждому элементу матрицы. В случае нулевых начальных условий X(0) = 0 и нулевой матрицы выхода системы D = 0 первое и второе слагаемое формулы Коши (4.2) равны нулю, откуда
![]() (4.7)
(4.7)
Фундаментальная матрица в символьной форме выглядит как
 .
.
Для определения подынтегрального выражения (4.7) вычисляют:
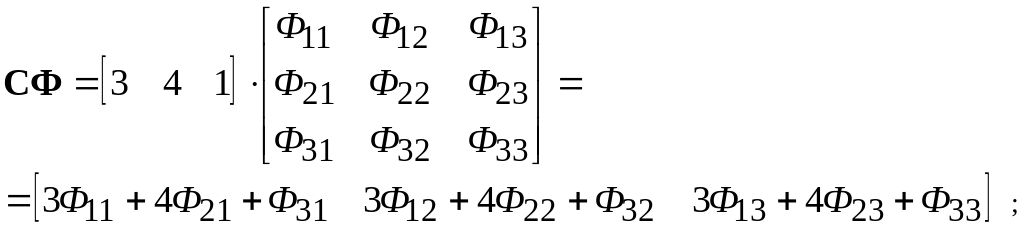
 СФВU
= [3Ф13
+ 4Ф23
+ Ф33][1]
= [3Ф13
+ 4Ф23
+ Ф33]
=
СФВU
= [3Ф13
+ 4Ф23
+ Ф33][1]
= [3Ф13
+ 4Ф23
+ Ф33]
=
=
![]() .
.
Выходную величину системы определяют из выражения (4.7):
![]()
Решение матричного интегрального уравнения
![]()
![]()
График переходной функции (рис. 4.2) определяют следующим образом
t=0:0.01:1;
y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);
plot(t,y).
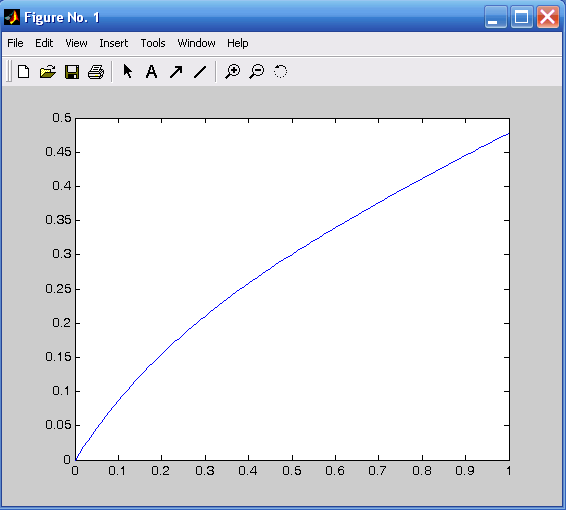
Рис. 4.2. Переходная функция модели, определенная методом прямого программирования
Метод параллельного программирования
При разложении передаточной функции (4.3) методом Хевисайда:
![]() (4.8)
(4.8)
(4.9)
С учетом выражения (4.8) получена схема моделирования (рис. 4.3).

Рис. 4.3. Схема моделирования системы методом параллельного программирования
 (4.10)
(4.10)
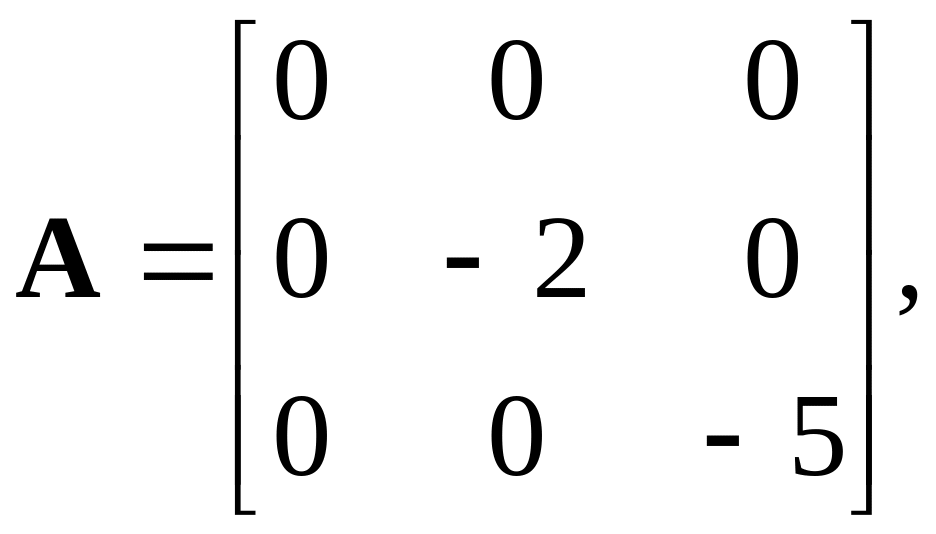
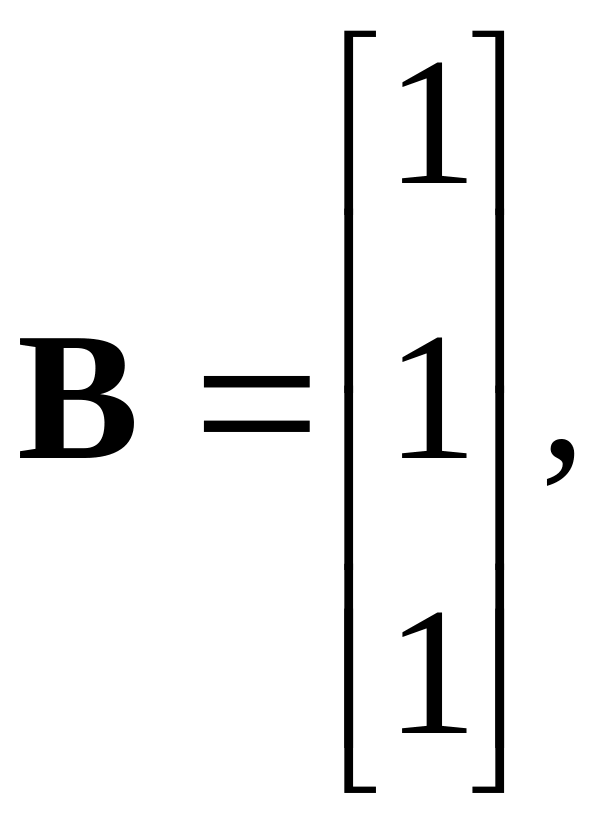
![]() D
= 0.
D
= 0.
Матрица A при параллельном программировании имеет диагональный вид, что достигается выбором базиса, при котором фазовые координаты не влияют друг на друга.
Определяют фундаментальную матрицу Ф(t):
A=[0,0,0;0,-2,0;0,0,-5] %Матрица состояния
syms s %Символьная переменная
Is=[s,0,0;0,s,0;0,0,s] %Единичная матрица
F=inv([Is]-[A]) %Обратная матрица в частотной области
F1=ilaplace(F) %Обратная матрица во временной области.
Фундаментальная матрица в частотной области

и во временной области
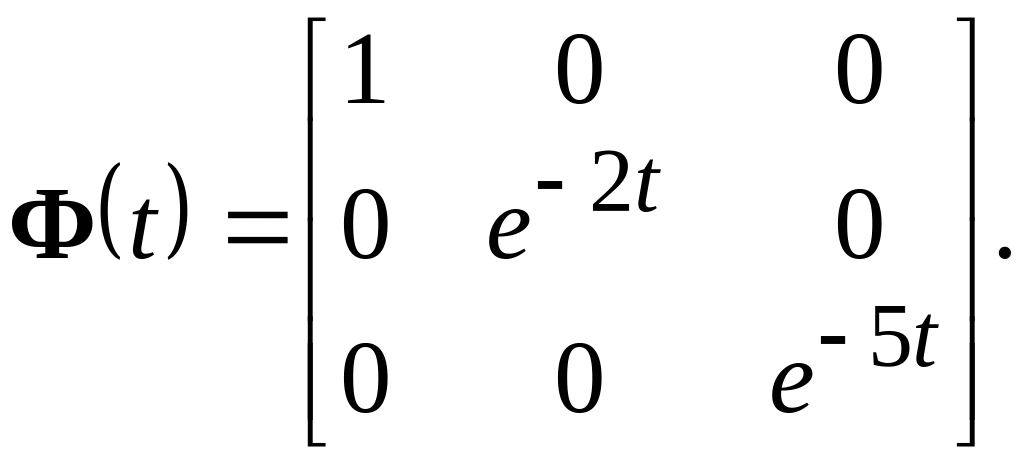

![]()
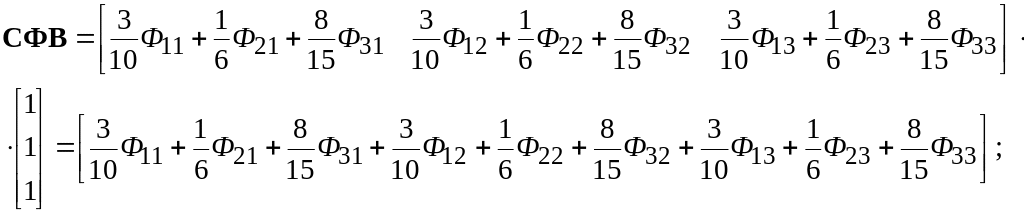

Решение матричного интегрального уравнения
![]()
График переходной функции (рис. 4.4) определяют следующим образом
t=0:0.01:1;
y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);
plot(t,y).
Метод последовательного программирования
Структурную схему для последовательного программирования получают из передаточной функции (4.5), если ее разбить на блоки и для каждого блока представить схему моделирования
![]() (4.11)
(4.11)
По блочной передаточной функции (4.11) составляют схему моделирования (рис. 4.5)
Из схемы моделирования (рис. 4.5) получена матрица коэффициентов состояния А и матрица коэффициентов наблюдения С
или
![]()
Рис. 4.4. Переходная функция модели, определенная методом параллельного программирования
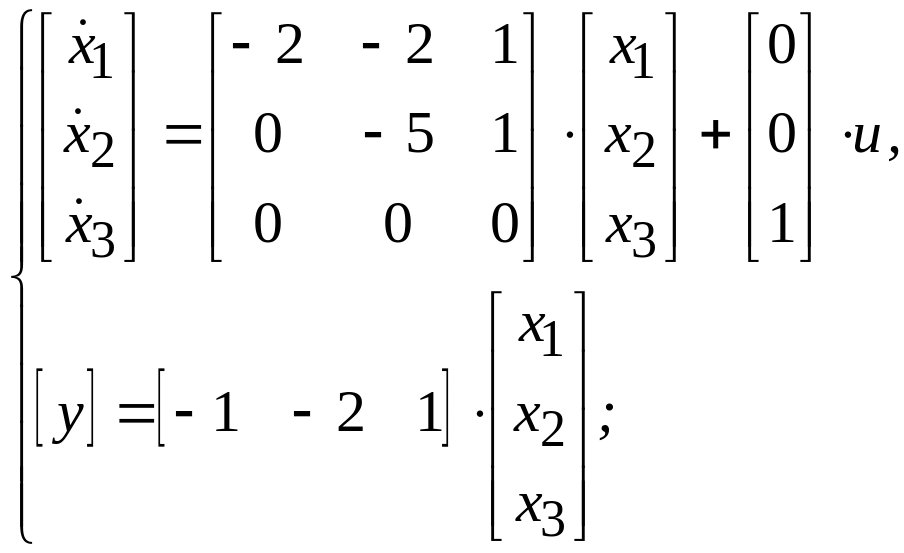 (4.12)
(4.12)
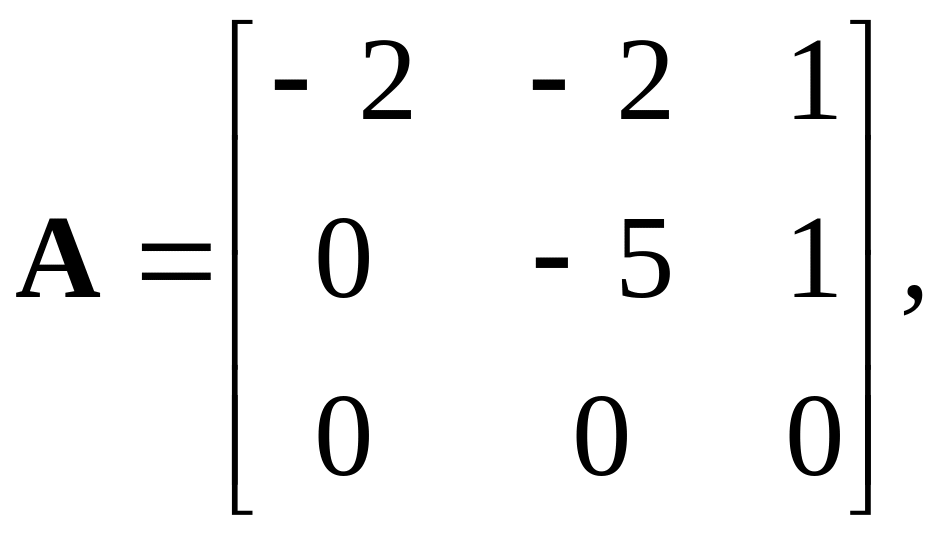 C
= [-1 -2 1],
D
= 0.
C
= [-1 -2 1],
D
= 0.
Определяют фундаментальную матрицу Ф(t):
A=[-2,-2,1;0,-5,1;0,0,0] %Матрица состояния
syms s %Символьная переменная
Is=[s,0,0;0,s,0;0,0,s] %Ввод единичной матрицы
F=inv([Is]-[A]) %Обратная матрица в частотной области
F1=ilaplace(F) %Обратная матрица во временной области.
Рис. 4.5 Схема моделирования системы методом последовательного программирования
Фундаментальная матрица в частотной области

и во временной области




Решение матричного интегрального уравнения
График переходной функции (рис. 4.6) определяют следующим образом
t=0:0.01:1;
y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);
plot(t,y).
Рис. 4.6. Переходная функция модели по методу последовательного программирования
Задание
1. По полученным в лабораторной работе №3 схемам моделирования заданной передаточной функции и матрицам состояния А для методов прямого, параллельного и последовательного программирования определить обратные матрицы в частотной и временной области.
2. С помощью полученных ранее матриц коэффициентов А, В, С и обратных матриц в частотной и временной области для методов прямого, параллельного и последовательного программирования определить произведение матриц CФBU, используя Matlab.
2. Определить
![]() для
методов прямого, параллельного и
последовательного программирования.
Построить графики Y(t).
для
методов прямого, параллельного и
последовательного программирования.
Построить графики Y(t).
Содержание отчета
Структурные схемы исследуемой системы, полученные методами прямого, параллельного и последовательного программирования.
Расчет обратных матриц в частотной и временной области для методов прямого, параллельного и последовательного программирования.
Расчет выходного сигнала для методов прямого, параллельного и последовательного программирования.
Графики выходного сигнала для методов прямого, параллельного и последовательного программирования.
Контрольные вопросы
1. Дайте сравнительную характеристику фундаментальных матриц, полученных по методу параллельного программирования и методу прямого программирования.
2. Дайте сравнительную характеристику фундаментальных матриц, полученных по методу параллельного программирования и методу последовательного программирования.
3. Основные свойства фундаментальной матрицы.
4. С помощью какой команды может быть получена обратная матрица в частотной области?
5. С помощью какой команды может быть получена обратная матрица во временной области?
6. Каким образом с помощью Matlab может получено подинтегральное выражение для определения выходного сигнала системы?
7. Каким образом можно записать фундаментальную матрицу в символьном виде?
