Лабораторная работа № 12 Определение амплитудно-фазовых характеристик дискретных систем

Цель работы

1. Рассмотрение методов определения АФХ дискретных систем.

2. Построение виртуальных моделей устройств определения АФХ дискретных систем.

3. Изучение процессов, происходящих в дискретных системах при квантовании сигнала по времени.

4. Экспериментальное определение АФХ дискретных систем.

Теоретическое обоснование

По частотным характеристикам дискретных систем, так же как и по частотным характеристикам непрерывных систем, определяется устойчивость и оценивается качество переходных процессов.

Используя критерий Найквиста можно определить устойчивость непрерывных САР по АФХ разомкнутой системы W(jω). Согласно этому критерию непрерывная система, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом состоянии, если АФХ разомкнутой системы не охватывала точку (–1, j0) при изменении ω от 0 до ∞. Этот же критерий можно применить и при исследовании дискретных систем, определив АФХ дискретной системы через АФХ непрерывной системы

, (12.1)

где W(jω), – АФХ непрерывной и дискретной систем.

Так как АФХ дискретной системы является периодической функцией частоты дискретизации ω_П, то для анализа устойчивости дискретной САР необходимо рассматривать АФХ только для частотного диапазона от 0 до ω_П/2. При подаче на вход дискретной системы круговой частоты, например ω, система, будет реагировать на комбинацию частот: ω, ω + ω_П, ω + 2ω_П, …, ω – ω_П, ω – 2ω_П, …

Таким образом, один вектор АФХ дискретной системы может быть построен по нескольким векторам АФХ непрерывной системы.

. (12.2)

Так как с возрастанием частоты амплитуда стремится к нулю, то в выражении (12.2) присутствуют конечное число слагаемых. Убывание составляющих выражения (12.2) определяется частотными свойствами непрерывной системы и частотой прерывания ω_П. В большинстве случаев без большой потери точности АФХ дискретной системы можно аппроксимировать первыми тремя членами, образующими выражение (12.2).

Проекции векторов, по которым строятся частотные характеристики непрерывных систем, определяются путем реализации выражений

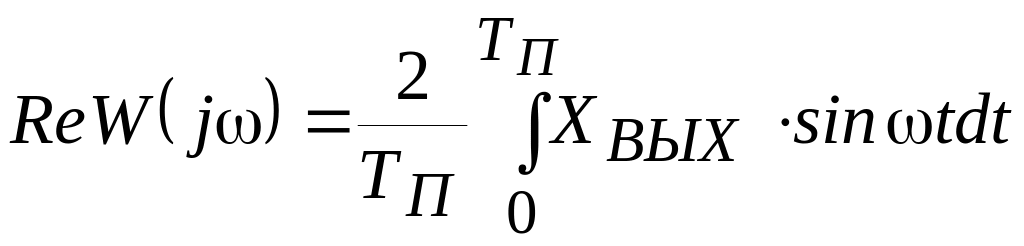(12.3)

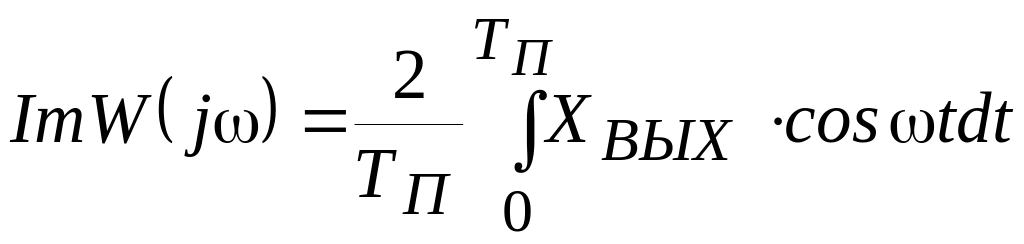(12.4)

где – это амплитуда выходного синусоидального сигнала.

Дискретная система также может быть исследована с помощью частотных характеристик, которые определяются через дискретное преобразование Лапласа.

Определим АФХ дискретной системы через АФХ непрерывной системы

. (12.5)

Выражение (12.5) можно представить через действительную и мнимую части спектра

, (12.6)

. (12.7)

Для построения соответствующих частотных характеристик дискретных систем необходимо выражения (12.5 – 12.7) преобразовать

, (12.8)

, (12.9)

, (12.10)

где n – натуральный ряд чисел n = 0, ±1, ±2, …, Т_П – интервал дискретности, _П – круговая частота работы дискретного элемента. Причём _П и Т_П связаны соотношением .

Сравнения выражений (12.5 – 12.7) с соответствующими выражениями (12.9 – 12.10) показывает, что если частотные характеристики непрерывных систем являются функциями частоты  и параметров системы, то частотные характеристики дискретных систем зависят от частоты , параметров системы, частоты работы дискретного элемента _П и натурального ряда чисел n. При подаче гармонического сигнала непрерывная система, согласно выражениям (12.5 – 12.7), реагирует на одну частоту и её реакция определяется параметрами системы регулирования. При подаче гармонического сигнала непрерывная часть дискретной системы согласно выражениям (12.8 – 12.10) реагирует на сумму частот , ( + _П), ( + 2_П), …, ( – _П), ( – 2_П), …, которые появилась в системе в результате работы дискретного элемента, и выходной сигнал непрерывной части дискретной системы определяется суммой реакций на ряд частот, полученных в результате модуляции. Наибольший вклад в реакцию дискретной системы вносят низкие частоты, и по мере увеличения порядкового номера гармоники n вклад соответствующей частоты уменьшается.

Выражения (12.8 – 12.10) позволяют обосновать метод экспериментального определения частотных характеристик дискретных систем. Реакция дискретной системы на гармонические колебания частоты , равносильна реакции непрерывной системы на комбинацию частот , ( + _П), ( + 2_П), …, ( – _П), ( – 2_П), …. Таким образом, для определения АФХ дискретной системы надо в этой системе оставить только непрерывную часть, на вход которой подать комбинацию частот.

Таким образом, устройство для определения АФХ дискретных систем состоит из нескольких устройств, определяющих АФХ непрерывной системы. Причем, одно устройство определяет частотные характеристики непрерывной системы на частоте ω, второе устройство – на частоте (ω + ω_П), третье – на частоте (ω + 2ω_П) и т. д.

Для непрерывной системы коэффициент передачи на частоте ω определяется как отношение вектора выходного сигнала к вектору входного сигнала. Так же определяется и коэффициент передачи дискретной системы, но вектор выходного сигнала определяется как векторная сумма n векторов, каждый из которых определяемая реакцией на свою частоту. Причём, вектора (коэффициенты ряда Фурье), амплитудой которых можно пренебречь, отбрасываются.

Определим АФХ дискретной системы через дискретное преобразование Лапласа, которое запишем через дискретную импульсную переходную функцию. Для рассматриваемого примера дискретная импульсная переходная функция определяется как решетчатая функция от непрерывной импульсной переходной функции

. (12.11)

Выражение для определения дискретного преобразования Лапласа

. (12.12)

Подставляя в формулу (12.12) выражение (12.11) определим изображение выходной величины

. (12.13)

Осуществляя замену s = jω определяем частотные характеристики дискретных систем

, (12.14)

, (12.15)

. (12.16)

Хотя по внешнему виду выражения (12.8 – 12.10) отличаются от соответствующих выражений (12.14 – 12.16), выполненные по ним расчеты будут одинаковы. Для выражений (12.8 – 12.10) исходными данными являются АФХ непрерывной системы, а для выражений (12.14 – 12.16) исходными данными являются параметры непрерывной системы.

Описание работы

Согласно выражениям (12.3) и (12.4) на рис. 12.1 приведена структурная схема устройства по определению АФХ непрерывной системы лабораторная работа № 2). Устройство содержит: 1 – блок задающего сигнала; 2 – исследуемую систему, заданную передаточной функцией; 3, 4 – блоки умножения; 5 – блок задания коэффициента 2/Т_П; 6, 7 – блоки, определяющие периоды тестового сигнала; 8, 9 – пороговые устройства, определяющие период интегрирования; 10 – логический блок; 11, 12 – интеграторы; 13,14 – блоки, фиксирующие результаты измерения; 15 – блок формирования косинусного сигнала.

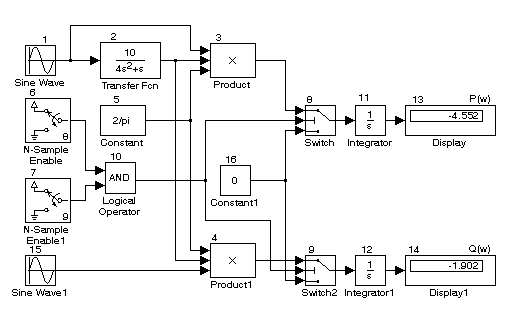
Рис. 12.1. Структурная схема устройства по определению АФХ непрерывной системы

с определением периода интегрирования

На рис. 12.2а представлена структурная схема устройства для определения проекций АФХ дискретных систем только в одной точке.

Устройство состоит из трех подсистем, в которых определяются проекции АФХ непрерывных систем на действительную и мнимую оси для трех частот: ω₁ = ω, ω₂ = ω + ω_П, ω₃ = ω + 2ω_П (ω =2, ω_П = 4). Подсистемы отличаются параметрами настройки, определяемыми частотой тестового сигнала.

Входящие в подсистемы блоки Subsystem (рис. 12.2б) выполнены в соответствии со структурной схемой рис.12.1.

Так как всегда ω_П > ω, то при n < 0 аргумент функции W(jω) принимает отрицательные значения. Учитывая, что Р() четная функция, то изменение знака аргумента не изменяет знак Р(). В то же время проекция АФХ дискретной системы на мнимую ось Q() при n < 0 изменяет свой знак.

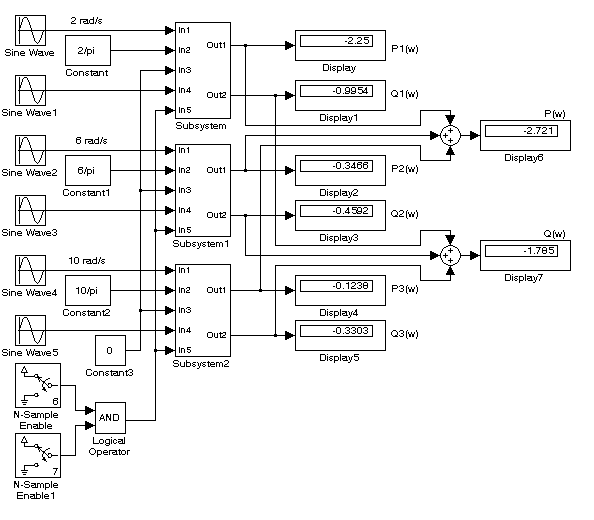
а)

б)

Рис. 12.2. Структурная схема устройства для определения проекций АФХ дискретной системы на действительную и мнимую оси при n > 0.(ω₁ = 2 рад/с; ω_П = 4 рад/с)

Таким образом, для определения действительной и мнимой составляющих вектора АФХ дискретной системы на одной частоте ω при n > 0 необходимо в структурной схеме (рис. 12.2) выполнить следующие операции:

– в генераторах тестовых сигналов задать частоты ω, ω + ω_П, ω + 2ω_П;

– в блоках Sine Wave в параметрах настройки фазы установить pi/2;

– в соответствии с заданными частотами ввести константы в блоки Constant;

– определить проекции вектора АФХ дискретной системы на действительную и мнимую оси;

– определить суммы проекций вектора АФХ дискретной системы на действительную и мнимую оси.

Для определения действительной и мнимой составляющих вектора АФХ дискретной системы на одной частоте ω при n < 0 необходимо в структурной схеме (рис. 12.2) выполнить следующие операции:

– изменить частоты в генераторах тестовых сигналов согласно выражениям ω, ω – ω_П, ω – 2ω_П;

– в соответствии с новыми частотами ввести константы в блоки Constant;

– изменить параметр настройки фазы косинусного блока с pi/2 на –pi/2;

– определить проекции вектора АФХ дискретной системы на действительную и мнимую оси;

– определить суммы проекций вектора АФХ дискретной системы на действительную и мнимую оси.

Для определения второй точки необходимо изменить частоту тестового сигнала, пересчитать параметры устройств и провести измерения, используя вышеописанный алгоритм.

Частотные характеристики непрерывных и дискретных систем можно получить не только экспериментальным, но и теоретическим путем. С помощью пакета Control System Toolbox можно строить частотные характеристики систем в обычном и логарифмическом масштабах рис. 12.3 и 12.4.

h=tf(10,[4,1,0]) %Исходные данные, заданные в форме TF

wp=4; %Частота дискретизации

t=2*pi/wp; %Интервал дискретности

hd=c2d(h,t) %Преобразование непрерывной передаточной

%функции в дискретную

figure(1) %Построение логарифмических характеристик

bode(h,hd),grid on %непрерывной и дискретной систем

figure(2) %Построение АФХ характеристик

nyquist(h,hd),grid on %непрерывной и дискретной систем.

На рис. 12.4 представлены структурные схемы, состоящие из апериодического звена и запоминающего элемента нулевого порядка, на который подается гармонический сигнал. Период дискретизации у всех формирующих элементов одинаков и равен 0,628 с, что соответствует частоте 10 рад/с.

.

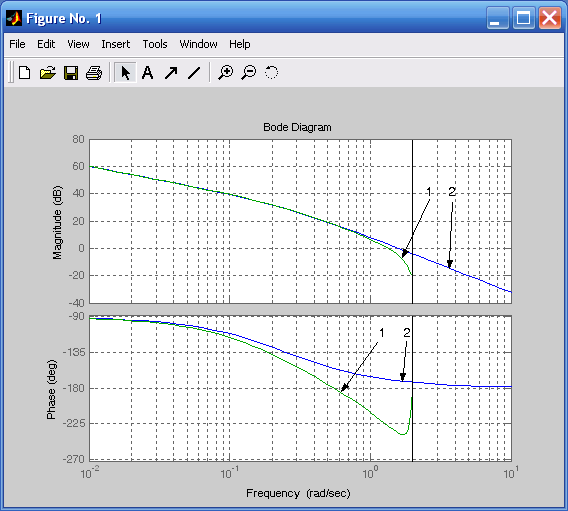
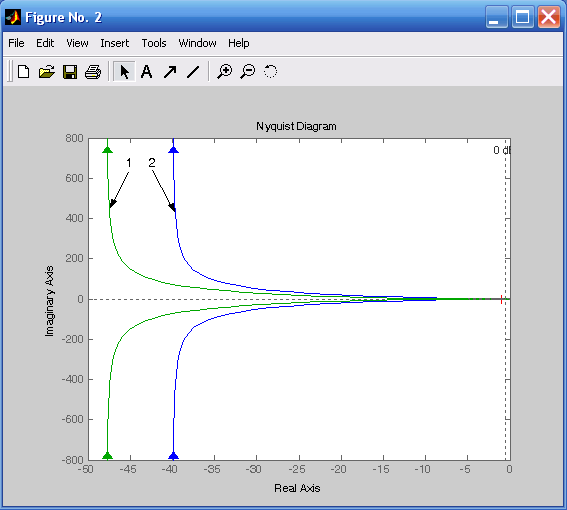
1 – дискретная система, 2 – непрерывная система

Рис. 12.3. Частотные характеристики непрерывных и дискретных систем

Рис.12.4. Определение АФХ дискретной системы

Исходя из основного тестового сигнала 1 рад/с и частоты дискретизации, равной 10 рад/с, на рис. 12.4 представлены схемы, на входы которых подаются частоты ω, ω + ω_П, ω + 2ω_П, ω – ω_П, ω – 2ω_П. Осциллограммы показывают (рис. 12.5), что реакция системы на разные частоты одинакова, то есть изменение частоты входного сигнала в низкочастотном диапазоне вызовет такую же реакцию, как соответствующее изменение входной частоты в области высоких частот.

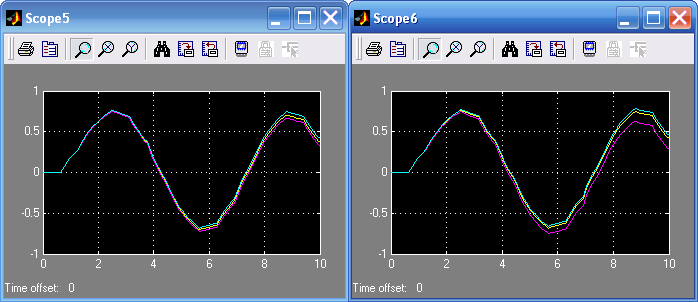
Рис. 12.5. Результаты моделирования дискретной системы

Запоминающий элемент (устройство выборки-хранения) вносит искажения в систему. Для определения частотных характеристик запоминающего элемента нулевого порядка перейдем от передаточной функции

(12.17)

к частотным характеристикам

. (12.18)

Из выражения (12.18) определяем фазовую

и амплитудную

(12.19)

характеристики запоминающего элемента нулевого порядка.

На рис. 12.6 представлена структурная схема устройства, позволяющая определять частотные характеристики запоминающего элемента экспериментальным путем.

Рис. 12.6. Структурная схема устройства для определения частотных характеристик

запоминающего элемента

Устройство, изображенное на рис. 12.6А, позволяет определять частотные характеристики исследуемых блоков по упрощенному алгоритму, а устройство, изображенное на рис. 12.6В, определяет частотные характеристики по более точному алгоритму.

Задание

1. Для заданной передаточной функции и заданных частотах работы дискретной системы (табл.1) определить параметры настраиваемых блоков (рис. 12.2).

2. Построить структурные схемы устройств, определяющие АФХ дискретной системы.

3. Определить частотные характеристики исследуемой системы.

4. С помощью пакета Control System Toolbox построить частотные характеристики дискретной системы, полученной путем преобразования заданной непрерывной системы (рис. 12.3).

5. Определить АФХ заданной системы (табл. 2) по схеме (рис. 12.4).

6. Для заданного варианта определить параметры устройства (рис. 12.6), определяющего частотные характеристики запоминающего элемента.

Содержание отчета

1. Структурные схемы устройств, определяющих АФХ дискретных систем.

2. Теоретические расчёты частотных характеристик дискретных систем с использованием непрерывных передаточных функций и импульсных переходных функций.

3. Результаты моделирования частотных характеристик.

4. Временные диаграммы, поясняющие работу формирующего (запоминающего) элемента нулевого порядка.

5. Частотные характеристики запоминающего элемента нулевого порядка, полученные экспериментальным и теоретическим путем.

6. Выводы.

Контрольные вопросы

1. Как изменяются параметры гармонического сигнала при прохождении через линейную систему (звено)?

2. Как строится АФХ непрерывных систем?

3. Как определяются проекции вектора выходного сигнала непрерывной системы?

4. Как определяются проекции вектора выходного сигнала дискретной системы?

5. Как можно определить АФХ дискретной системы, если известны АФХ непрерывной системы?

6. Как изменится связь между АФХ дискретной системы и АФХ непрерывной системы, если увеличится частота работы дискретного элемента?

7. Какими свойствами характеризуется Р(ω) и как эти свойства используются в устройствах по определению АФХ дискретной системы?

8. Какими свойствами характеризуется Q(ω) и как эти свойства используются в устройствах по определению АФХ дискретной системы?

9. Как отразится на результатах эксперимента малое время задержки?

10. Как по АФХ дискретной разомкнутой определить её устойчивость в замкнутом состоянии?

11. Как определяются частотные характеристики на выходе дискретной системы, по её непрерывной передаточной функции?

12. Обоснуйте методику экспериментального определения амплитудно-фазовой характеристики дискретной системы.

13. Какие изменения вносит запоминающий элемент нулевого порядка в частотные свойства передаточного сигнала.