3.3 Основные особенности реализации мкэ в SolidWorks

Разработчики конечно-элементных программных комплексов (и любых других), как правило, заботясь об оригинальности и конфиденциальности кода, не предоставляют подробную информацию о реализованных в них вычислительных методах, что превращает программу в своеобразный “черный ящик”. Однако использование программы в отсутствие представлений о происходящих в ней процессах может привести к неадекватным результатам ее использования даже при наличии соответствующей математической подготовки пользователя.

Поэтому для увеличения степени прозрачности производимых вычислений необходимо предоставить некоторую информацию, которую возможно получить либо используя навыки программирования, либо обращаясь в службу поддержки разработчика, либо на основании литературы по интересуемому и смежному программному обеспечению, сопутствующих руководств, справок, статей [91].

Ниже, опираясь на последний способ, будет прояснены некоторые особенности реализации МКЭ для решения статической задачи в SolidWorks:

1) деформации по умолчанию принимаются упруго малыми; конструктивная нелинейность не поддерживается;

2) дискретизация объема на конечные элементы происходит: для объемного тела – на тетраэдры с гранями, аппроксимируемыми линейными и параболическими функциями координат; для поверхностных моделей – плоскими или криволинейными треугольниками;

3) перемещения и усилия вычисляются в вершинах КЭ (для линейных КЭ), а также около середин сторон или ребер КЭ (для параболических КЭ);

4) для пространственных КЭ степенями свободы являются 3 перемещения вдоль осей системы координат (рис. 23а), для оболочечных КЭ – степенями свободы являются также 3 угла поворота нормали к срединной поверхности (рис. 23б), для балочных КЭ – 3 перемещения и 3 поворота вокруг осей (рис. 23в), для стержневых КЭ – 3 перемещения вдоль осей (рис. 23г);

Рис. 23 – Конечные элементы SolidWorks: а – тетраэдальный КЭ второго порядка; б – треугольный КЭ второго порядка; в – балочный КЭ; г – стержневой КЭ

5) матрица жесткости образуется на основании модуля Юнга и коэффициента Пуассона ;

6) на основе компонентов напряженно-деформированного состояния и параметров прочности материала производится вычисление эквивалентных напряжений по избранному критерию прочности [90];

7) результаты удовлетворяют принципу минимума потенциальной энергии деформации;

8) проблема интегрирования по объему сложной формы или криволинейной поверхности разрешается выражением элементарного объема в локальной системе координат, связанной с КЭ:

, (74)

где , , - локальные координаты, связанные с КЭ; - матрица Якоби (якобиан преобразования), использующаяся также для оценки правильности КЭ [92].

3.3.1 Решатели в SolidWorks

В SolidWorks доступны прямой и итерационный решатели.

Итерационный решатель обладает большей скоростью вычислений (особенно с числом узлов более ), позволяет решать нелинейные задачи. Согласно МКЭ нелинейные проблемы формулируются системой нелинейных алгебраических уравнений вида:

, (76)

где - неизвестные перемещения; - общие внешние воздействия в узлах. Задача состоит в определении неизвестных , зависящих от .

В итерационных методах аппроксимация решения проводится при общем нагружении, без разбиения нагрузки на части, имеющей место быть в инкрементальных методах. В каждом последующем шаге (итерации) предполагается, что матрица жесткости постоянна. В связи с этим появляются неуравновешенные (остаточные) нагружения, отступления от равновесия. После каждой итерации определяют неуравновешенные нагружения и учитывают при следующей итерации. Действия повторяют, пока все условия равновесия не будут удовлетворены с необходимой точностью.

В итерационном решателе SolidWorks реализованы обычный и модифицированный методы Ньютона-Рафсона для корректировки параметров, описывающих состояние системы.

Если - приближенное решение системы нелинейных уравнений, то его улучшают, если вектор-функция остаточных сил раскладывается в ряд Тейлора вблизи :

, (77)

где - функция остаточных сил, - инкрементное (приращенное) перемещение.

Также учитывается условие, что исправленное решение отвечает условиям равновесия, т.е.:

. (78)

Тогда справедливо:

(79)

где - тангенциальная матрица жесткости.

После определения определяют из выражения:

. (80)

Итерационный метод Ньютона-Рафсона ведет к быстрой сходимости решения и обладает высокой устойчивостью. Но при каждом повторном шаге необходимо вычислять матрицу жесткости системы и решать новую систему уравнений, что увеличивает его вычислительную стоимость. Для устранения этого недостатка используется модифицированный метод Ньютона-Рафсона, предполагающего, что матрица в ходе итерации не меняется:

, (81)

где - тангенциальная матрица нулевой итерации и вектора .

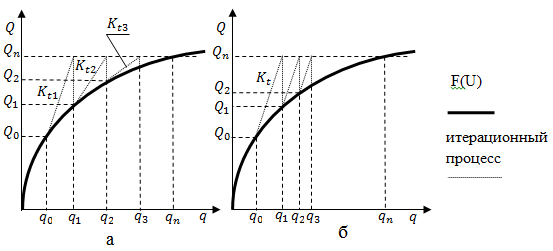
Рис. 24 – Пояснительные иллюстрации к итерационному методу Ньютона-Рафсона: а – обычный метод; б - модифицированный

Порядок итерации формально остается прежним с той разницей, что вместо применяется . Различие состоит в том, что в этом случае необходимо также на первом шаге решить систему уравнений, а в каждой следующей итерации выполнять поправку правой части уравнения с :

. (82)

Модифицированный метод Ньютона-Рафсона значительно экономичнее обычного несмотря на более медленную сходимость, потому чаще используется [84, 92].

Описание методики расчетов в программах анализа динамики

Динамические модели, используемые для исследования вибронагруженности двухосных автомобилей.

Одной из первых работ, где на теоретическом уровне была поставлена проблема снижения вибронагруженности конструкций автомобилей, является учебник Е. А. Чудакова [ ]. В нем приведена простейшая одномассовая модель автомобиля, представляющая собой массу, совершающую вертикальные колебания на пружине. Одномассовая модель, ввиду своей простоты, удобна для детального исследования и поэтому широко использовалась в последующих исследованиях, вплоть до настоящего времени [ ].

Например, в работе [ ] рассматриваются различные варианты одномассовых моделей: без учета неподрессоренной массы и амортизатора, с учетом амортизатора, без учета и с учетом жесткости шины. При этом воздействие со стороны дороги не учитывается. Проведенное сравнение показывает, что расчеты по подобным упрощенным схемам позволяют получить только низшую частоту, на которой влияние неподрессоренных масс и сопротивления амортизатора незначительно [ ].

При использовании одномассовой схемы необходимо учитывать следующие допущения [ ]. Все неподрессоренные массы автомобиля составляют в среднем 12-20 % от массы подрессоренных частей, а жесткость подвески в 5-10 раз меньше жесткости шин. В результате собственная частота колебаний неподрессоренных масс выше, чем подрессоренных. Поэтому их влияние при тех частотах, когда перемещения кузова значительны, мало, и им можно в первом приближении пренебречь. Тогда подрессоренная масса совершает колебания на двух последовательно соединенных пружинах разной жесткости, одна из которых моделирует упругие свойства подвески, а другая – шины. Их можно заменить упругим элементом с эквивалентной жесткостью.

При рассмотрении вертикальных и продольных угловых колебаний автомобиля в первом приближении используется одномассовая модель, в которой подрессоренная масса установлена на пружины, моделирующие упругие свойства передней и задней подвесок. При этом для простоты рассматриваются свободные незатухающие колебания системы, имеющие две степени свободы [ ].

Ряд авторов [ ] при рассмотрении одномассовых моделей учитывает не только все вышеописанные факторы, но и воздействие со стороны случайного микропрофиля дороги, задаваемого функцией изменения ординаты микропрофиля от времени, анализируя таким образом вынужденные колебания.

Статистический анализ колебаний подтвердил значительное влияние на вибронагруженность автомобиля изменений динамического положения равновесия подрессоренной массы, которые могут быть обусловлены, в частности, воздействием макропрофиля дороги (горные дороги, дороги на сильно пересеченной местности). Воздействие макропрофиля моделировалось в виде силы , приложенной в вертикальном направлении к центру подрессоренной массы в дополнение к кинематическому возбуждению , описывающему микропрофиль дороги [ ].

Преимущество модели с “двойным” возбуждением (кинематическим и динамическим ) состоит в том, что появляется возможность учета не только вертикальных воздействий макро- и микропрофиля дороги, но и поперечных сил, действующих на автомобиль с мягкой подвеской в реальных условиях движения: центробежных сил на поворотах, боковых порывов ветра и т.п. [ ]

В конструкциях некоторых автомобилей и шасси применяется безрессорная подвеска. Колебательная система, эквивалентная безрессорной подвеске колес, при слабой связи колебаний передней и задней частей надколесной массы представляется в виде соответствующей массы, установленной на пружине с параллельно включенным демпфером [ ]. При этом жесткость пружины соответствует суммарной жесткости шин передних или задних колес, а демпфер учитывает силы неупругого сопротивления в шине. Что касается названной выше массы, то имеется в виду масса, приведенная к оси соответствующих колес. При этом, как правило, осуществляется расчет как свободных колебаний системы, так и вынужденных, определяемых случайной функцией изменения ординат микропрофиля дороги.

Более точные результаты расчетов удается получить, применяя двухмассовые модели, учитывающие не только подрессоренную, но и неподрессоренную массы, приходящиеся на переднюю и заднюю оси [ ]. В такой схеме упругие и демпфирующие свойства подвески моделируются пружинами и демпферами. Возможен учет дорожного воздействия [ ]. В работе [ ], кроме того, учитывается сухое межлистовое трение в рессоре.

В работах [ ] двухмассовая колебательная система используется для рассмотрения вопроса о влиянии крепления амортизаторов на колебания. При этом учет жесткостей втулок достигается введением дополнительной пружины, соединяющей шток демпфера с подрессоренной массой. Использование резиновых втулок несколько повышает вибронагруженность, но уменьшает вероятность отрыва колес от дороги вследствие уменьшения диапазона частот, при котором происходит отрыв, и смещения этого диапазона в сторону больших частот возбуждения [ ].

При рассмотрении вышеописанных моделей использовалось допущение о том, что коэффициент распределения подрессоренных масс в продольной плоскости равен единице. В этом случае инерционная связь между вертикальными колебаниями передней и задней частей подрессоренной массы пренебрежимо мала, и ее можно не учитывать [ ].

Основой для оценки вибронагруженности подавляющего большинства легковых, грузовых автомобилей и автобусов является трехмассовая модель двухосной машины. Она позволяет выявить некоторые особенности колебания корпуса и установить практически важные зависимости между параметрами и характеристиками системы подвески. К этой модели зачастую можно свести многие симметричные подвески многоосных машин [ ]. Кроме того, эта модель значительно проще, чем модель многоосной машины, а ее анализ и расчет не вызывают больших затрат времени у конструктора и ЭВМ.

Как отмечается в работе [ ], рассмотрение всех движений подрессоренной массы (подергивание, пошатывание, подпрыгивание, покачивание, галопирование, рыскание) в первом приближении не обязательно, так как известно, что при прямолинейном движении пошатывание, покачивание и рыскание невелики, что объясняется высокой боковой жесткостью шин и практически неупругой в этом направлении связью мостов с подрессоренной системой. Подергивания подрессоренной массы возникают, главным образом, при резком торможении или разгоне. При движении с установившейся скоростью подергивания не ощущаются, так как силы инерции подрессоренной массы, направленные вдоль оси , несопоставимо велики в сравнении с горизонтальными составляющими реакций дороги, возникающими при наезде колес на неровности.

В связи с тем, что у автомобилей обычной компоновки подрессоренная масса полностью симметрична относительно продольной плоскости, проходящей через центр тяжести вдоль оси , боковые и поперечные колебания не вызывают других колебательных движений. Поэтому они обычно рассматриваются самостоятельно [ ].

Таким образом, при построении основной эквивалентной колебательной системы, учитывающей главные, определяющие вибронагруженность, колебательные движения, достаточно отразить в ней только факторы, вызывающие вертикальные колебания и угловые колебания в продольной плоскости.

В работе [ ] указывается, что если жесткость крепления агрегата к раме сравнительно мала, и его парциальные частоты колебаний на подвеске попадают в интересующий нас диапазон 0,7-22,4 Гц, то целесообразно учесть такой резонанс и считать соответствующую массу упругоприкрепленной к раме. Приводится схема, учитывающая податливость опор кабины и двигателя.

При выборе линейных моделей используется ряд допущений [ ]. В частности, считается, что профили дороги под правым и левым колесами каждого моста идентичны (а поэтому оба эти колеса заменяют одним [ ]). Однако реальное случайное воздействие со стороны дороги нельзя считать симметричным и, следовательно, требуется рассмотрение нелинейной пространственной колебательной модели [ ]. При этом приходится отказаться от допущения о симметричности автомобиля относительно продольной плоскости, проходящей через его центр тяжести [ ].

Современные критерии оценки вибронагруженности приводят к необходимости уточнения математических моделей транспортных машин, в частности, учета податливости их несущих систем [ ] и, в первую очередь, податливости на кручение. В основном это относится к расчету вибронагруженности длиннобазных автомобилей, но у транспортных машин с нормальной и даже короткой базой, имеющих рамную конструкцию несущей системы, упругие свойства последней сказываются на колебаниях автомобиля и на оценке его вибронагруженности [ ]. В первую очередь, влияет податливость несущей системы на кручение [ ]. Например, поперечные угловые ускорения в различных сечениях несущей системы автомобиля могут различаться в несколько раз. Это объясняется тем, что жесткость несущей системы на кручение соизмерима и даже иногда меньше поперечной угловой жесткости подвесок автомобиля [ ].

Изгибная жесткость несущей системы также может сказываться на оценке вибронагруженности. В работе [ ], например, экспериментально показано, что у автомобиля Урал-337 увеличение изгибной жесткости рамы позволяется уменьшить угловые колебания кабины и продольные ускорения ее точек в два раза. По данным работы [ ], на вибронагруженность определяющее влияние оказываются первая и вторая формы изгибных колебаний рамы автомобиля и колебания передней части кабины.

Вибронагруженность оценивается по колебаниям в ограниченной полосе частот от 0,7 до 22,4 Гц. Это позволяет использоваться или модель автомобиля, состоящую из сосредоточенных масс, соединенных упругими и демпфирующими элементами (дискретную модель), или модель с распределенными параметрами, в которой учитываются те собственные формы колебаний, для которых частоты попадают в указанный диапазон [ ].

Дискретные модели колебаний автомобилей, в которых подрессоренные и неподрессоренные массы рассматриваются как твердые тела, к настоящему времени хорошо разработаны и широко используются [ ].

Модель автомобиля с несущей системой, упругой на кручение, впервые была рассмотрена в работе [ ], где подрессоренные массы представлялись в виде двух масс, сосредоточенных над подвесками и соединенных упругими и демпфирующими элементами, моделирующими упругость и трение в несущей системе автомобиля. Анализ этой модели показывает, что в ней может быть учтен лишь первый тон упругих колебаний несущей системы. Однако в большинстве случаев этого недостаточно для уточненной оценки вибронагруженности [ ]. В работе [ ] эта модель была развита таким образом, что предлагалось разбить подрессоренную массу на несколько масс, упруго связанных при кручении и жестко связанных при изгибе.

В настоящее время существуют исследования, где рассматриваются различные модели колебаний транспортных машин с учетом податливости их несущих систем при изгибе и кручении [ ]. Так, например, в работе [ ] предлагается несущую систему грузового автомобиля моделировать упругим стержнем с переменными погонной массой и жесткостью. Распределение масс и жесткостей соответствует распределению этих параметров у несущей системы автомобиля. Однако удовлетворительные результаты при расчете кручения рам лестничного типа получаются лишь в том случае, когда при расчете используют жесткостные параметры несущей системы при кручении, полученные экспериментально [ ]. Эти модели дают возможность получать хорошие результаты при расчете изгибных колебаний несущей системы и крутильных колебаний рам хребтового типа и несущих корпусов.

Целесообразно иметь такую модель несущей системы автомобиля с рамой лестничного типа, которая позволила бы получить уточненные оценки общей и местной нагруженности системы, не используя экспериментальные данные по жесткости рам на кручение, а опираясь только на конструктивные параметры несущей системы. Поэтому в работе [ ] предлагается моделировать несущую систему уже не одним упругим стержнем, а системой стержней. Лонжероны и поперечины в этом случае представлены тонкостенными стержнями, которые работают в соответствии с теорией В.З.Власова, согласно которой при изгибе стержней деформация сдвига и инерция поворота отсутствуют, а при стесненном кручении принято, что форма поперечных сечений не меняется, и отсутствуют деформации сдвига срединной плоскости.

Следует отметить, что моделирование несущей системы является достаточно сложной задачей [ ]. Даже одна рама автомобиля представляет собой статически неопределимую упругую систему, расчет которой весьма сложен и разрабатывается в работах [ ]. Установка агрегатов на раму автомобиля вносит дополнительную сложность и неопределенность в расчет несущей системы.

Наиболее полное решение задачи анализа вибронагруженности конструкции автомобиля может быть получено с использованием метода конечных элементов [ ]. В этом случае в пространственную нелинейную систему автомобиля включается конечно-элементная модель несущей системы. В качестве основных расчетных моделей рам грузовых автомобилей применяют стержневые конечно-элементные модели и комбинированные оболочечно-стержневые конечно-элементные модели. В первом случае рама моделируется системой стержневых конечных элементов, связанных между собой в точечных узлах. При использовании же комбинированных конечно-элементных моделей отдельные элементы конструкции моделируются оболочечными, а пролеты балок – стержневыми конечными элементами.

Как отмечается в работе [ ], в несущих системах автомобиля широко используются тонкостенные пространственные элементы открытого профиля. Информация о конечном элементе тонкостенного стрежня включает свойства материалов, размеры поперечного стержня включает свойства материалов, размеры поперечного сечения, эксцентриситетов в соединениях, узловых податливости, тип матрицы жесткости [ ]. В настоящее время для моделирования систем используются конечные элементы, построенные на аппроксимации полей перемещений [ ]. Однако для удовлетворительного описания НДС автомобильных конструкций требуется создавать дискретные модели с огромным числом конечных элементов и степеней свободы [ ].

Прочность и жесткость тонкостенных конструкций открытого профиля определятся плоским напряженным состоянием их элементов [ ]. Существенное повышение эффективности расчета пространственных тонкостенных систем достигается при использовании конечных элементов, построенных на аппроксимации напряжений.

Таким образом, развитие метода конечных элементов позволило создавать сложные конечно-элементные модели, состоящие из стержневых и плоских элементов, не только для всего автомобиля [ ], но и для выполнения статистических расчетов его рам на изгиб и кручение, с учетом гипотезы В.З. Власова для тонкостенных стержней открытого профиля [ ].

[6]

При движении в естественных дорожных условиях машина совершает случайные колебания, а ее узлы и детали подвергаются динамическим нагрузкам. Характер и интенсивность указанных процессов зависят как от конструктивных параметров, так и от условий движения. Дорога представляет собой поверхность со случайным расположением неровностей в продольной и поперечной плоскостях. Для упрощения вычислений вероятностных характеристик дорожная поверхность может быть определена двумя случайными функциями – ординатой среднего сечения по длине и углом наклона поперечного сечения :

, (4)

, (5)

где , - функции высот микропрофиля сечений поверхности дороги соответственно под левым и правым колесами относительно некоторого среднего значения; - колея машины; - текущая ордината.

Некоррелируемость функций и подтверждается практически. В общем случае эти функции являются нестационарными и их характеристики меняются по времени и длине участка дороги. Если же оцениваемый участок дороги по типу покрытия и степени износа однороден и можно пренебречь их изменениями во времени, то функции, определяющие поверхность дороги, считают с некоторым приближением как случайные стационарные с нормальным законом распределения, подчиняющиеся эргодической системе.

Рассмотрим условия стационарности и эргодичность случайного процесса.

Случайный процесс называется стационарным, если его вероятностные закономерности неизменны во времени. Свойство стационарности в корреляционной теории случайных процессов выражается постоянством математического ожидания и дисперсии ; и независимостью корреляционной функции от начала отсчета (где ).

Определение статических характеристик случайного процесса в общем случае предполагает достаточно большой ансамбль реализаций. Однако для стационарного случайного процесса имеется возможность получения вероятностных характеристик по одной достаточной продолжительности реализации при эргодичности процесса.

Случайный процесс считается эргодическим, если результат осреднения какой-либо характеристики процесса по множеству реализаций совпадает с результатом осреднения закона изменения этой характеристики по одной реализации. Для математического ожидания достаточным условием эргодичности является стремление при ; для корреляционной функции кроме достаточного условия необходимо, чтобы закон распределения ординат случайного процесса был нормальным. Оценки математического ожидания, дисперсии, среднего квадратического отклонения, корреляционной функции определяются выражениями:

, (6)

, (7)

, (8)

где - продолжительность реализации процесса; - среднее квадратическое отклонение; - центрированная случайная функция, .

Математическое ожидание определяет изменение случайной функции на какую-то среднюю величину, а разброс значений относительно среднего характеризует дисперсия. Корреляционная функция дает представление о вероятностной связи между значениями микропрофиля по длине участка дороги. Чем быстрее функция стремится к нулю, тем слабее взаимосвязь между последующими значениями . Значение , при котором , называется максимальным интервалом корреляции. По виду корреляционной функции можно выявить скрытую периодическую составляющую со случайной амплитудой, которая обычно характеризует состояние дороги.

В корреляционной теории стационарных случайных процессов наряду с приведенными выше характеристиками широко используется еще один вид статистических характеристик – спектральные плотности процессов. Спектральная плотность дисперсий высот неровностей микропрофиля дороги характеризует частоту повторения неровностей со случайной амплитудой и данной длиной волны. Определяется спектральная плотность как преобразование Фурье от корреляционной функции:

, (9)

где - частота повторений неровностей микропрофиля дороги; ; - длина волны гармонической составляющей микропрофиля дороги.

Применяя формулу обратного преобразования Фурье, можно по спектральной плотности установить корреляционную функцию:

. (10)

Так как корреляционная функция в точке равна дисперсии, то согласно (10) она представляет площадь под кривой с масштабным коэффициентом и может быть определена через спектральную плотность:

. (11)

Если поверхность дороги рассматривать как случайную функцию одного переменного вдоль дороги, среднее значение микропрофиля равно нулю и величина мала по сравнению с продолжительностью реализации (протяженность обследуемого участка), то оценка корреляционной функции (8) заменяется практически эквивалентной и более простой формулой:

. (12)

Так как корреляционная функция является неслучайной функцией, то полученная по результатам эксперимента она может быть представлена аналитическим выражением. Ее нормированное значение хорошо аппроксимируется зависимостью:

, (13)

где , во многих случаях ; и - коэффициенты, характеризующие степень нерегулярности микропрофиля; - частота скрытой периодичности в случайной функции микропрофиля дороги.

Интегрированием выражения нормированной корреляционной функции можно определить спектральную плотность распределения высот неровностей микропрофиля дороги:

. (14)

Нормированное значение спектральной плотности:

. (15)

Нормирование корреляционной функции и спектральной плотности применяется для придания результатам большей наглядности и удобства их использования при исследованиях и расчетах. Спектральная плотность может быть также определена различными способами непосредственно по данным измерений.

Интенсивность колебаний при движении по неровным дорогам существенно зависит от скорости движения. Для описания воздействия дороги необходимо в вероятностных характеристиках перейти от функций протяженности, определяющих потенциальные свойства микропрофиля, к функциям по времени. Для корреляционной функции это достигается заменой переменной на при : , где - скорость движения. Переход спектральной плотности во временную область можно осуществить, с учетом связи между пространственными и временными частотами ( , где - круговая частота) путем изменения масштабов по осям координат: и . Значит, замена переменных в выражениях корреляционной функции и спектральной плотности приводит к трансформации графиков при постоянстве дисперсии [3]:

. (16)

Для точной оценки усталостной прочности необходимо рассматривать все значимые случаи нагружения – стационарные или нестационарные. Стационарный случай нагружения – прямолинейное движение с постоянной скоростью по дороге определенного типа и постоянным коэффициентом сопротивления движению. Остальные случаи – нестационарные. При расчете стационарных случаев нагружения с использованием линеаризованных конечно-элементных моделей обычно пользуются частотными методами, например, спектральным анализом, а для исследования нестационарных процессов или стационарных с учетом нелинейных характеристик необходимо использовать методы решения во временной области. В зависимости от типа анализа используются разные способы задания дорожного воздействия.

При использовании частотных методов дорожное воздействие целесообразно задавать в виде матрицы взаимных спектральных плотностей. При этом принимаются следующие допущения: 1) колеса имеют двустороннюю связь с дорогой, то есть не отрываются от опорной поверхности при колебательных процессах; 2) контакт колеса с дорогой точечный.

При решении задач усталостной прочности во временной области дорожное воздействие задается в виде дискретной функции перемещений или сил в узлах. Конечно-элементная модель автомобиля требует для проведения динамических расчетов пространственную модель дорожного воздействия.

Стационарное дорожное воздействие.

Допускается, что случайная функция продольного микропрофиля дороги является нормальной и стационарной. Это позволяет применять для описания различного типа дорог методы корреляционной теории случайных процессов, в соответствие с которыми для формирования модели дорожного воздействия необходимо располагать такими статистическими характеристиками микропрофиля как спектральная плотность и взаимная спектральная плотность высот неровностей правой и левой колеи.

В отечественной литературе имеется небольшое количество данных по измерениям микропрофиля дорог различных типов. При этом практически всегда измерения проводились по одной колее, поэтому данных для получения пространственной модели дорожного воздействия недостаточно.

Исходя из гипотезы изотропности поля дорожного воздействия предложена зависимость, по которой можно получить взаимную корреляционную функцию двух колей дороги , располагая корреляционной функцией микропрофиля одной колеи [18]:

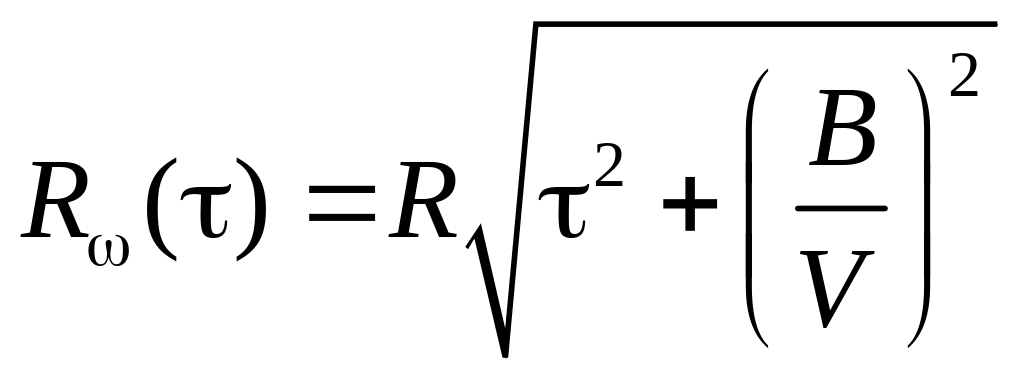
где - ширина колеи автомобиля, - скорость.

Вычислив , с помощью преобразования Фурье, можно получить взаимную спектральную плотность:

Таким образом, если задаться скоростью движения автомобиля, его базой и статистическими характеристиками дороги, полученными по результатам замера высот неровностей одной колеи можно сформировать модель пространственного дорожного воздействия.

При ее моделировании необходимо дополнительно учесть временное запаздывание между мостами автомобиля. При наличии запаздывания функция взаимной спектральной плотности будет:

, для колес одной колеи,

, для колес разных колей,

где - время запаздывания между мостами и .

Используя представление комплексной формы через тригонометрическую:

;

;

или

;

,

где и - синфазный спектр, и - квадратурный спектр.

Для использования метода спектрального анализа необходимо представить воздействие в виде матрицы взаимных спектральных плотностей. Если пронумеровать колеса начиная с переднего левого, потом переднее правого и т.д., то для двухосного автомобиля:

,

где - функция спектральной плотности микропрофиля, - функции взаимной спектральной плотности между и колесами.

Приведем несколько характерных примеров определения элементов матрицы при такой нумерации:

;

;

;

где - расстояние между мостами автомобиля.

При заполнении матрицы из-за недостатка экспериментальных данных остается затруднение с получением функции спектральной плотности микропрофиля . Остановимся подробно на самом распространенном методе расчетного определения этой функции. Существует несколько способов аппроксимации спектральной плотности микропрофиля дорожного полотна. Общепринятым является выражение:

, или более точное

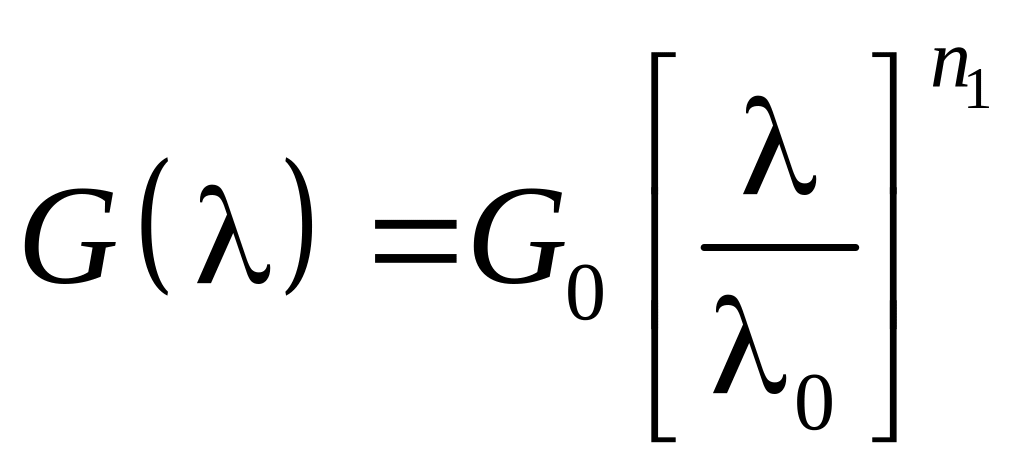при ; при ;

где - волновая частота, - значение спектральной плотности микропрофиля на частоте рад/м.

Частота и волновая частота связаны простой зависимостью:

.

На диаграмме с координатами зависимость представляет собой прямую линию, причем аппроксимации микропрофиля дорог разного типа оказываются практически параллельны друг другу.

Область спектральных плотностей микропрофиля, на которых возможна эксплуатация транспортных средств, ограничена параллелограммом, границы которого пересекаются:

1) минимально возможной высотой неровностей микропрофиля дороги, достижимой при существующем уровне развития строительной техники;

2) высотой неровности, при которой невозможно движение транспортного средства;

3) минимальной (10 см) и максимальной (100 м) протяженностью неровности (длиной волны), частота воздействия от которой при средних эксплуатационных скоростях движения на дорогах определенного типа соответствует полосе частот собственных колебаний подрессоренных и неподрессоренных масс автомобиля.

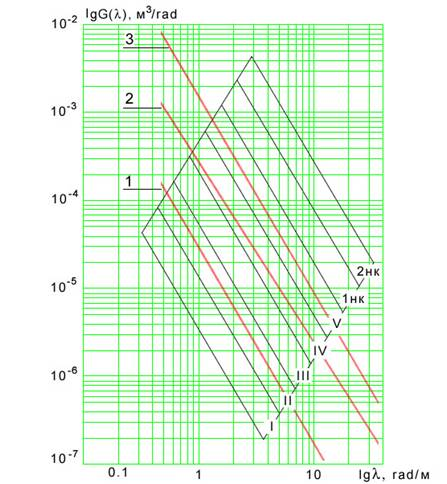
Полученный диапазон возможных спектральных плотностей микропрофилей был поделен на семь категорий дорог, позволяющий отразить характер их воздействия на долговечность несущих конструкций автомобиля: I – скоростные автомагистрали; II – автомагистрали; III – шоссе в плохом состоянии; IV – булыжные и гравийные дороги; V – грунтовые дороги; 1нк – лесные и сильно разбитые грунтовые дороги; 2нк – местность.

Если теперь необходимо получить функцию спектральной плотности микропрофиля дороги, а экспериментальные данные отсутствуют, достаточно задаться ее категорией, и варьируя значения коэффициентов уравнения добиться, чтобы прямая оказалась в требуемой области диаграммы.

Колеса грузовых автомобилей имеют большой диаметр, и, следовательно, большое пятно контакта с дорогой, которое сглаживает небольшие по протяженности неровности дороги, поэтому при расчетах желательно учитывать сглаживающую способность шин. Для этого необходимо либо ограничить минимальную длину волны, например, 20 см, либо вычислять размер пятна контакта в зависимости от радиуса колеса, давления в шинах и нагрузки на ось автомобиля. Это означает, что необходимо ограничить расчетный частотный диапазон в зависимости от длины пятна контакта и скорости движения автомобиля . Если ограничить длину волны воздействия длиной пятна контакта, то:

,

а, ограничивая частоту, получим:

.

Исходя из сказанного выше, алгоритм численного построения дорожного воздействия в частотной области выглядит следующим образом:

1) Исходными данными являются: аппроксимация спектральной плотности , скорость автомобиля и положение точек воздействия (база и расстояния между мостами);

2) С помощью обратного преобразования Фурье из получают корреляционную функцию воздействия ;

3) Получить взаимную корреляционную функцию ;

4) Преобразованием Фурье из получить взаимную спектральную плотность ;

5) Сформировать матрицы и .

Дальнейшее исследование в настоящей работе заключалось при использовании статистических данных о распределении пробега автомобилей по видам дорог и зависимости распределений скоростей движения автомобиля по времени на различных видах дорог – определить относительное время действия процесса нагружения при заданной скорости движения и, считая, что в определенном диапазоне скорости (2,5 км/ч) изменение скорости не оказывает существенного влияния на НДС, в частотной области спектральным методом проведены расчеты. В результате получены – спектральная плотность напряжений и характеристики случайного процесса изменения напряжений: среднеквадратическое отклонение, эффективная частота и коэффициент нерегулярности процесса. [17]

При движении автомобиля все его узлы подвергаются различного рода динамическим воздействиям, которые обусловлены неровностями дорожного полотна. Для анализа ресурса автомобиля в целом и отдельных его составляющих необходима оценка возникающих колебательных процессов. Для того чтобы расчетным путем определить характеристики сопротивления усталости, необходимо располагать адекватными моделями воздействия на систему (автомобиль) со стороны дорожного полотна. Так как автомобиль может двигаться по всевозможным типа дорог, то требует большое количество аппроксимаций дорожного полотна, так как автомобиль подвергается различного рода воздействиям при движении по дорогам различных типов. Кроме того, сложно сформировать такое воздействие, которое описывало бы движение автомобиля при движении с постоянной скоростью, разгоне, переезде единичных неровностей, торможение и т.д.

Одна из таких разработок заключается в учете взаимосвязи между левой и правой колеями дорог, что поможет более точно описать динамику движения транспортного средства.

С учетом зависимости между колеями дороги математически более адекватно отражают реальное дорожное воздействие. Так как использование зависимости Доддса не требует каких-либо дополнительных данных, т.е. достаточно располагать спектральной плотностью для одной колеи, то рекомендуется этот метод [19].

Обзор методов используемых для расчета отклика линейных систем на гармоническое воздействие.

Задача о нахождении отклика линейных систем на гармоническое воздействие сходится к решению системы дифференциальных уравнений:

, (1)

где , , - симметричные матрицы масс, демпфирования, жесткости соответственно; λ – частота вынуждающей силы, для различных значений частоты вынуждающей силы.

После разделения переменных система (1) сводится к системе линейных уравнений:

. (2)

Прямой метод решения.

Для каждой системы (2) прямым методом для каждого значения частоты вынуждающей силы формируется матрица динамической жесткости:

, (3)

Отклик вычисляется путем решения системы уравнений для каждого значения вынуждающей силы:

. (4)

Преимущества метода: высокая точность, легкость использования в любом диапазоне частот вынуждающей силы. Недостатки: высокие вычислительные затраты, невозможность строгого учета диссипативных свойств конструкции.

А т.к. как правило, матрица демпфирования неизвестна, то на практике для учета диссипации приходится использовать пропорциональную модель демпфирования. То есть строят матрицу , основываясь на матрице масс или жесткости: или , что может привести к различиям между расчетным и реальным откликом системы.

Модальный метод решения.

Решение – в 2 этапа. Первый этап – нахождение собственных частот и собственных векторов системы (2) с нулевой правой частью в нужном частотном диапазоне. При этом выполняются условия ортогональности:

, (5)

. (6)

На втором этапе происходит построение решения в виде:

, (7)

где - диагональная матрица, составленная из , где и - собственные частоты и декременты затухания соответственно.

Преимущества: более быстрый расчет, возможность учета диссипативных свойств реальной конструкции. Недостатки: потеря точности расчета, в связи с учетом ограниченного числа собственных тонов колебаний системы. [12]

В качестве исходной информации вводится описание формализованных характеристик воздействия внешней среды на транспортное средство. Применительно к машинам, предназначенным для эксплуатации на местности вне обустроенных дорог, возникает необходимость задания комплекса факторов внешнего воздействия, в частности:

1) Двумерного поля микропрофиля местности, описывающего воздействие на ходовую часть со стороны левой и правой колеи (функции изменения высоты микропрофиля под j-ой подвеской i-го борта ). Кинематическое возбуждение микропрофиля определяет общий уровень и характер динамических процессов в системе, а также накладывает ограничение на скорость движения машины в связи с вибрационным воздействием на экипаж;

2) Дорожной кривизны (радиус поворота ), ограничивающей скорость движения автомобиля по заносу и приводящей к перераспределению усилий в ходовой системе и трансмиссии;

3) Макропрофиля трассы (угол подъема–спуска ), описывающего подъемы, спуски и накладывающего ограничения по тяговой и тормозной характеристикам;

4) Одиночных препятствий (выступы или впадины длиной и высотой или глубиной ), наличие которых на местности изменяет скорость движения и может вызвать пиковые нагрузки в ходовой системе;

5) Характеристик жесткости дорожного полотна (жесткость грунта ), определяющих условия взаимодействия движителя транспортной машины с грунтом и характер нагруженности элементов ходовой системы;

6) Характеристик процесса изменения сил сопротивления со стороны рабочего органа (главный вектор и главный момент );

7) Распределения переменных сил сопротивления грунта прямолинейному движению (коэффициент сопротивления ) и повороту (коэффициент сопротивления );

8) Параметров, описывающих условия наблюдения и оценивания факторов внешней среды человеком-оператором (расстояние видимости трассы ).

Поскольку методика имитационных ресурсных испытаний ориентирована на решение задач прочностной надежности, то итоговые результаты этапа исследований динамики машин необходимо представлять в виде обобщенных статистических характеристик силового и кинематического воздействия на подлежащие проверке высоконагруженные элементы конструкций. В связи с этим случайные функции обобщенных координат, получаемые в процессе численного интегрирования уравнений движения, преобразуются через передаточные функции в характеристики процессов изменения нагрузок и напряжения в конкретных узлах и деталях. Для этого в инженерной практике часто используют два подхода: первый применим к стационарным процессам, когда путем статистической обработки реализаций (например, по процедуре быстрого преобразования Фурье) могут быть получены обобщенные спектральные характеристики, а затем методами теории выбросов определены числовые параметры и законы распределения максимумов процесса изменения напряжений. Именно такие характеристики необходимы для решения задач прогнозирования прочностной надежности и ресурса. Второй подход не накладывает ограничений на стационарность исходного процесса. Подход предполагает определение эмпирических законов распределения амплитуд напряжений непосредственно из реализаций нестационарного процесса путем последовательного выполнения численных процедур и статистической обработки информации. [13]

К [8]:

Формирование модели дорожного воздействия может быть осуществлено по методике работы Шлейхера-Крылова. Согласно работе Лукинского пробег автомобилей по разным типам дорог Российской Федерации распределяется согласно таблице XXX. Нагруженность конструкции существенно зависит от скорости движения автомобиля. Ее трудно регламентировать количественно, поскольку она зависит от многих факторов. Статистические исследования позволили установить вероятные скорости движения автомобилей по различным типам дорог (Лукинский). Для расчетов можно пользоваться обобщенной качественной оценкой, связывающей тип дороги и скорости движения автомобиля.

Данные о скоростях движения автомобилей по различным типам дорог позволяют заключить, во-первых, что изменение скоростей движения автомобиля хорошо описывается нормальным законом распределения, во-вторых, существует нижнее значение скорости движения, определяемое минимальной скоростью устойчивого движения автомобиля и верхнее, определяемое техническими возможностями автомобиля и дорожными условиями

Используя эти данные и считая закон распределения мгновенных скоростей движения усеченным нормальным, можно определить математическое ожидание средней скорости движения автомобиля по разным типам дорог, среднее квадратическое отклонение средней скорости и с их помощью вычислить долю ς i от общего пробега автомобиля со скоростью Vi. Значение ς i вычисляется как вероятность появления случайной величины в заданном интервале значений. Если затем разделить относительную долю пробега ς i на скорость Vi и пронормировать, получим относительное время действия процесса нагружения i ξ в течениидействия процесса движения Т.

В качестве примера, в таблице 2 приведено относительное время действия процессов нагружения шаровой опоры поворотной цапфы переднего моста полноприводного 96 автомобиля КамАЗ-4310 при движении по трем типам дорог.

Следующим шагов в прогнозировании ресурса является расчетная оценка характеристик процесса изменения напряжений в исследуемых элементах конструкции для выбранных режимов (скорость движения) в эксплуатации.

Считая, что изменении скорости движения автомобиля в диапазоне +-2,5 км/ч не оказывает существенного влияния на НДС, при помощи МКЭ в частотной области, спектральным методом были проведены расчеты шаровой опоры. В результате для каждой скорости и типа дороги были получены спектральная плотность напряжений и характеристики случайного процесса изменения напряжения: среднеквадратическое отклонение, эффективная частота и коэффициент иррегулярности процесса.

Значение математического ожидания напряжения определялось из статического расчета, поскольку для несущих элементов автомобиля нагрузка от сил тяжести является средней величиной, относительно которой при движении автомобиля, от дорожного воздействия, непрерывно происходят колебания. [8]

Теория надежности

Успех и результативность прочностных расчетов зависит от полноты разработки трех основных проблем, представляющих: 1) внешние силы – методы определения значений и характера распределения и изменения во времени всех внешних по отношению к конструкции нагрузок, установление возможно наиболее неблагоприятных с точки зрения прочности сочетаний этих нагрузок; 2) внутренние силы – методы определения напряжений и деформаций, возникающих в элементах конструкции при действии заданных внешних нагрузок; 3) предельные состояния или допускаемые напряжения – факторы, влияющие на прочность элементов конструкции в эксплуатации, количественные значения предельно допустимых напряжений и деформаций с учетом механических характеристик материала и их стабильности, вида напряженного состояния, влияния внешней среды и др. [1]