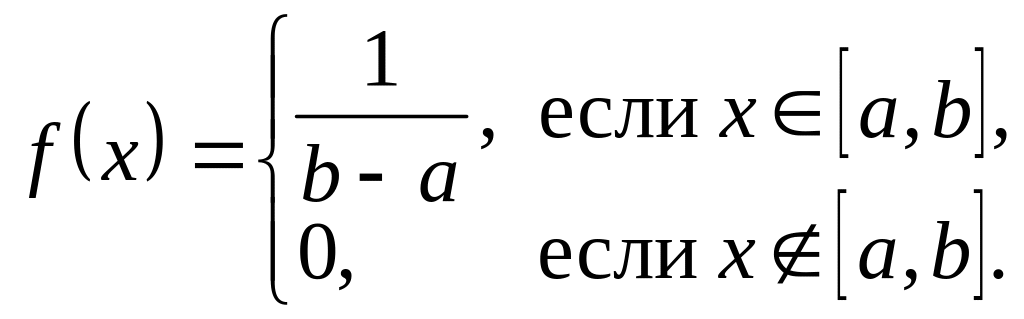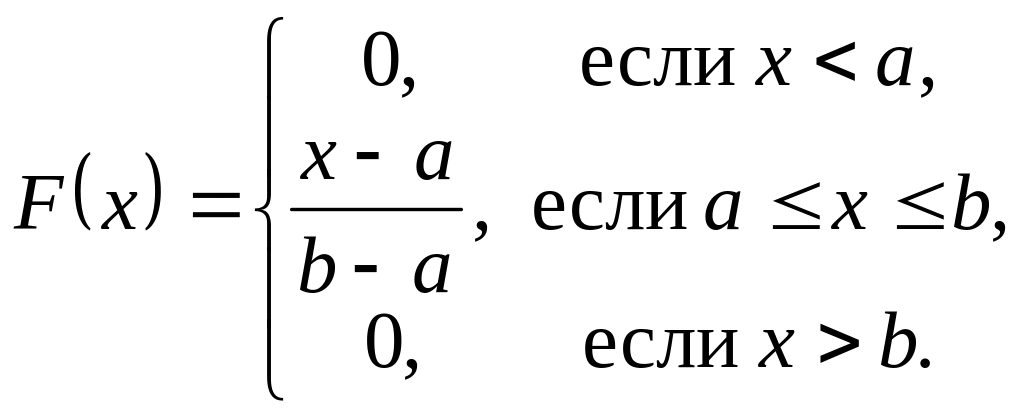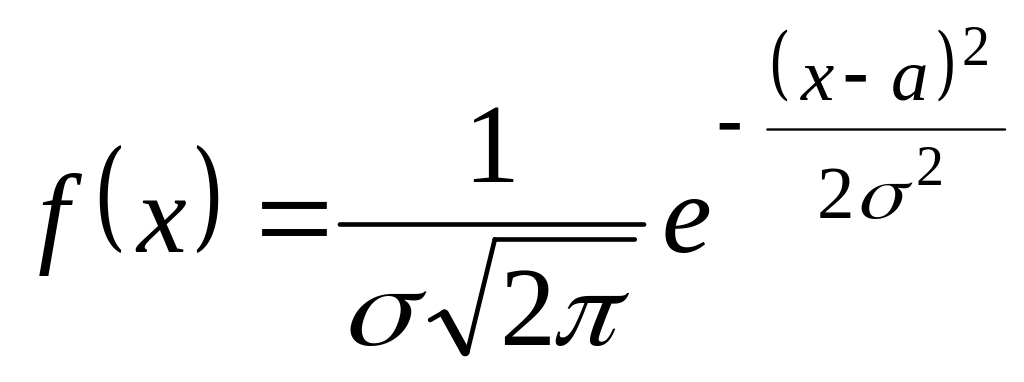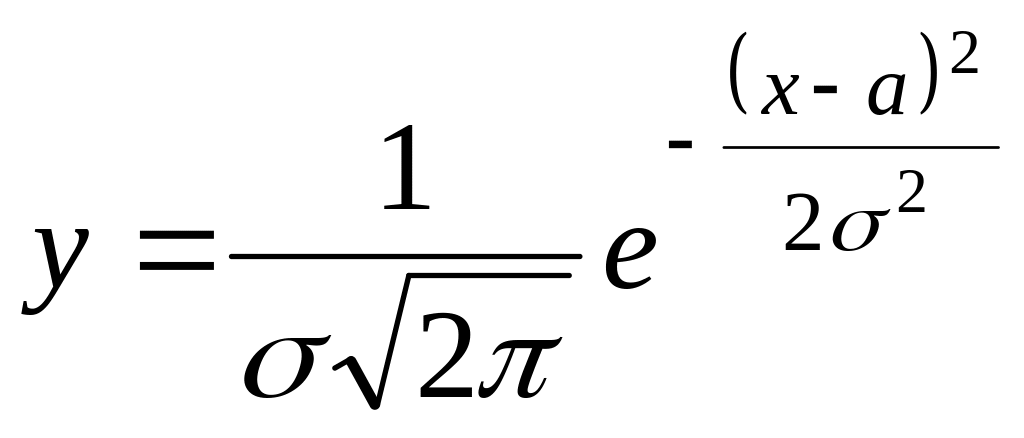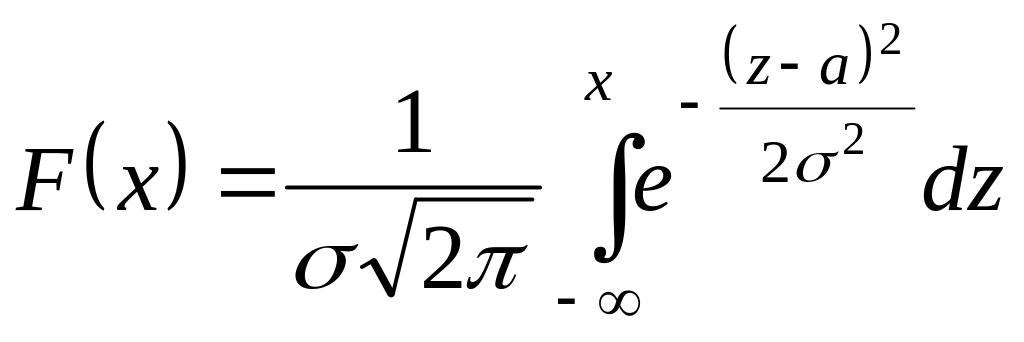- •4.7.2 Формула Пуассона.
- •4.7.3 Формулы Муавра-Лапласа.
- •4.7.4 Применение приближенных формул Пуассона и Муавра-Лапласа.
- •4.8 Случайные величины
- •4.9 Дискретные случайные величины
- •4.10 Функция распределения случайной величины. Плотность распределения непрерывной случайной величины.
- •4.11 Числовые характеристики случайной величины
- •4.12. Законы распределения дискретной случайной велисины
- •Биномиальное распределение
- •Распределение Пуассона
- •Простейший поток событий
- •Геометрическое распределение
- •Гипергеометрическое распределение
- •4.13 Законы распределения непрерывной случайной величины Равномерное распределение.
- •Нормальное распределение
- •Правило трех сигм.
Гипергеометрическое распределение
Пусть
в партии из
![]() изделий имеется
изделий имеется
![]() стандартных. Из партии случайно отбирают
изделий (каждое из которых может быть
извлечено с одинаковой вероятностью).
Обозначим через
случайную величину – число
стандартных. Из партии случайно отбирают
изделий (каждое из которых может быть
извлечено с одинаковой вероятностью).
Обозначим через
случайную величину – число
![]() стандартных изделий среди
отобранных. Очевидно, что случайная
величина
может принимать значения 0,1, …,
стандартных изделий среди
отобранных. Очевидно, что случайная
величина
может принимать значения 0,1, …,
![]() .
.
Для
того, чтобы найти вероятность того, что
случайная величина
![]() ,
используем классическое определение
вероятности. Искомая вероятность равна
отношению числа исходов, благоприятствующих
событию
,
используем классическое определение
вероятности. Искомая вероятность равна
отношению числа исходов, благоприятствующих
событию
![]() ,
к числу всех элементарных исходов
,
к числу всех элементарных исходов
![]() ,
т. е.
,
т. е.
|
(33) |
Гипергеометрическое распределение имеет вид
|
|
|
2 |
… |
|
… |
|
|
|
|
|
… |
|
… |
|
4.13 Законы распределения непрерывной случайной величины Равномерное распределение.
Равномерно
распределенная на отрезке
![]() случайная величина имеет плотность
распределения
случайная величина имеет плотность
распределения
|
(34) |
Функция распределения имеет вид
|
(35) |

Экспоненциальное распределение.
Случайная величина подчиняется экспоненциальному (показательному) закону, если она имеет плотность распределения
|
(32) |
где
![]() − параметр экспоненциального
распределения.
− параметр экспоненциального
распределения.
Функция распределения имеет вид
|
(33) |
Нормальное распределение
Нормальный закон («закон Гаусса») является предельным законом, т.е. к нему приближаются, при определенных условиях, другие законы распределения. Нормальный закон наиболее часто встречается на практике.
Нормальный закон распределения характеризуется плотностью распределения вероятностей вида:
|
(34) |
Нормальное
распределение определяется двумя
параметрами:
![]() и
и
![]() .
Вероятностный смысл этих параметров
следующий:
равно математическому ожиданию,
−
среднему квадратическому отклонению
нормального распределения. Если
.
Вероятностный смысл этих параметров
следующий:
равно математическому ожиданию,
−
среднему квадратическому отклонению
нормального распределения. Если
![]() и
и
![]() ,
то нормальное распределение называют
нормированным (стандартным) и
плотность нормированного распределения
имеет вид
,
то нормальное распределение называют
нормированным (стандартным) и
плотность нормированного распределения
имеет вид
|
(35) |
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию
|
|
1.
Область определения:
![]() при любом
при любом
![]() ,
график расположен выше оси
;
,
график расположен выше оси
;
2.
Асимптоты.
Ось
служит асимптотой графика функции
,
так как
![]() ;
;
3.
Экстремумы, интервалы возрастания и
убывания:
функция
имеет один максимум при
![]() ,
равный
,
равный
![]() Действительно,
Действительно,
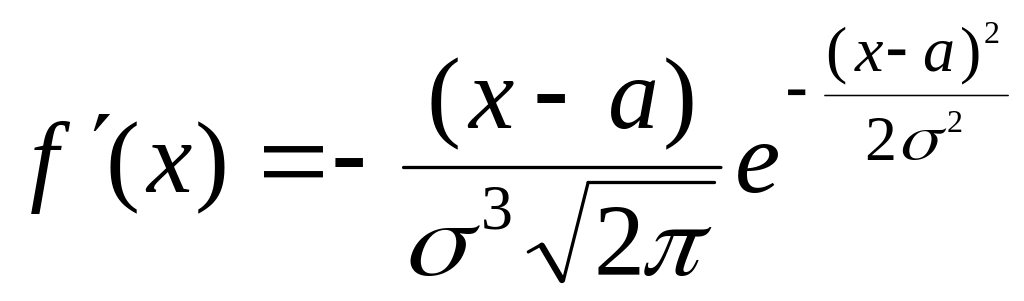 .
Отсюда
.
Отсюда
![]()
![]() при
,
при этом, если
при
,
при этом, если
![]() ,
то
,
то
![]() ,
а если
,
а если
![]() ,
то
,
то
![]() .
Отсюда
.
Отсюда
![]() точка максимума и
точка максимума и
![]() .
.
4.
Точки перегиба, интервалы выпуклости
и вогнутости:
точки
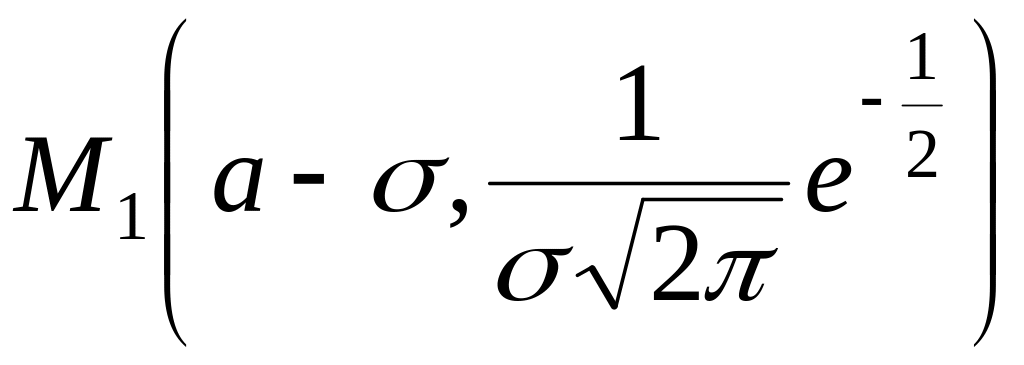 и
и
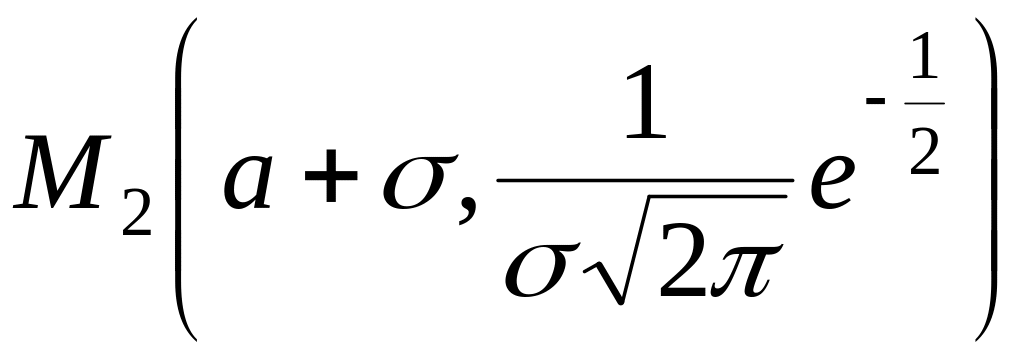 являются точками перегиба графика
функции
.
являются точками перегиба графика
функции
.
5. График.

При и нормальную кривую называют нормированной.
Функция нормального распределения имеет вид
|
(36) |
Функция
![]() нормированного
нормированного
![]() распределения имеет вид
распределения имеет вид
|
(37) |
Значения функции вычисляются с помощью функции :
|
(38) |
Функцию
можно выразить через функцию
Лапласа

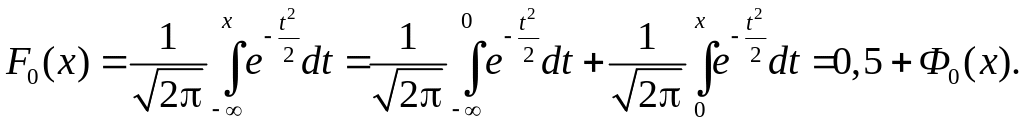 (39)
(39)
Функция нормального распределения также выражается через функцию Лапласа:
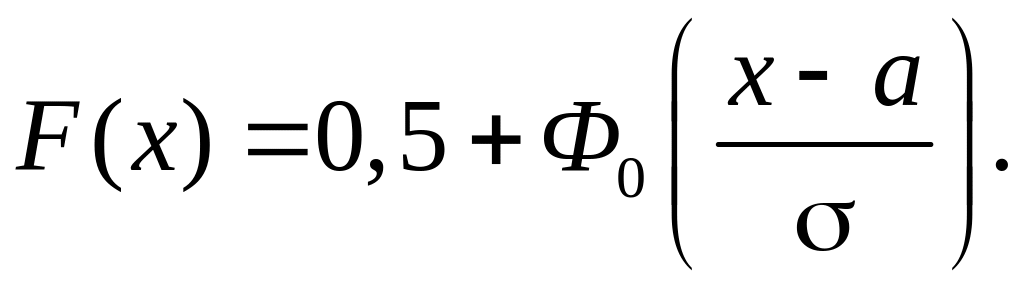 (40)
(40)
Вероятность
попадания в интервал
![]() нормальной случайной величины
равна
нормальной случайной величины
равна
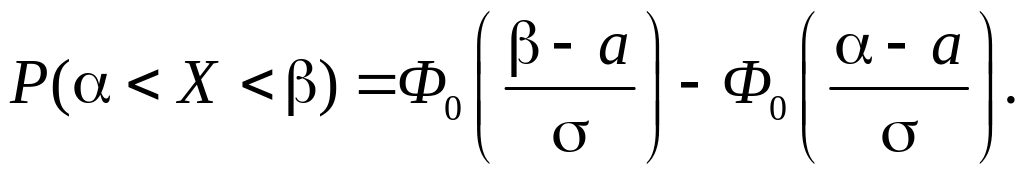 (41)
(41)
Вероятность
того, что отклонение нормально
распределенной случайной величины
от математического ожидания
по абсолютной величине меньше заданного
положительного числа
![]() равна
равна
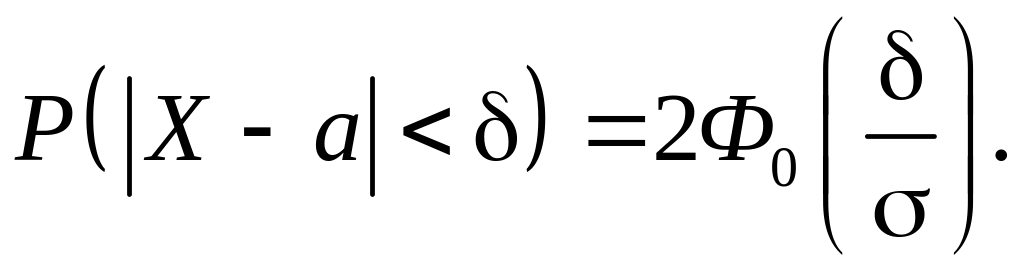 (42)
(42)

 .
.
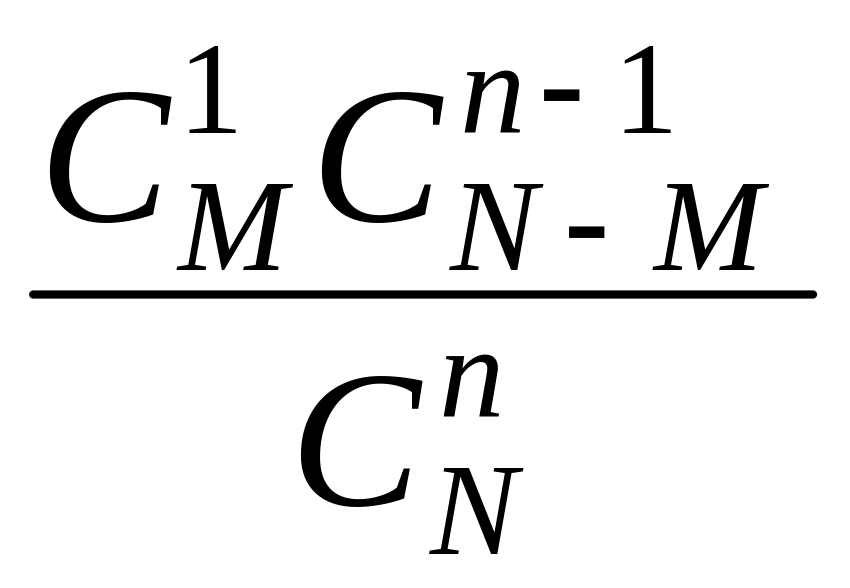

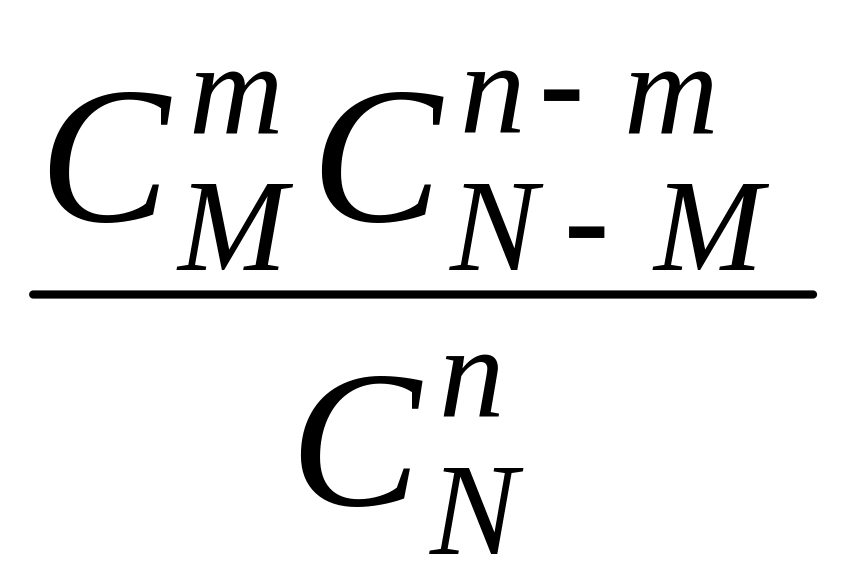
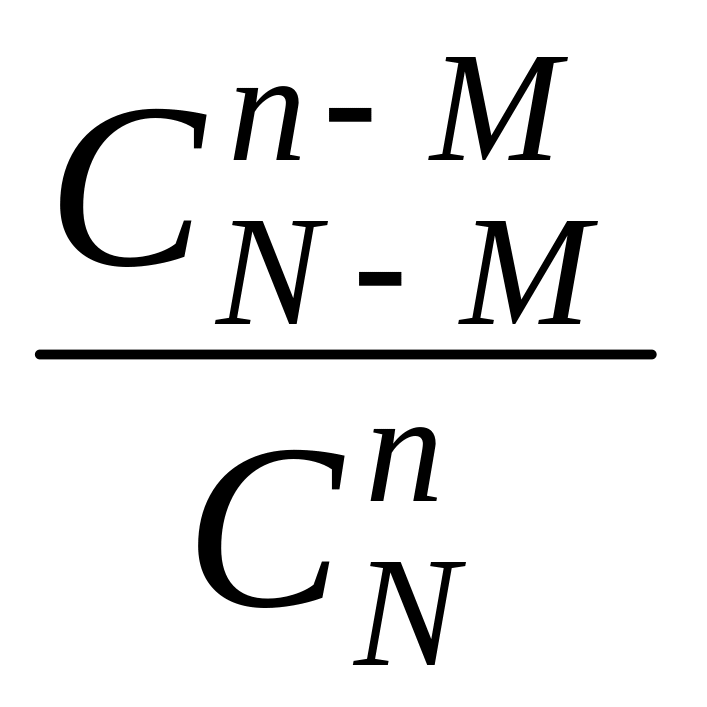 или
или