4.12. Законы распределения дискретной случайной велисины

_{Законы распределения случайной величины:}

1. _{для дискретной случайной величины: биномиальный (схема Бернулли), распределение Пуассона (формула Пуассона), геометрическое - вероятности образуют геометрическую прогрессию; гипергеометрическое распределение}

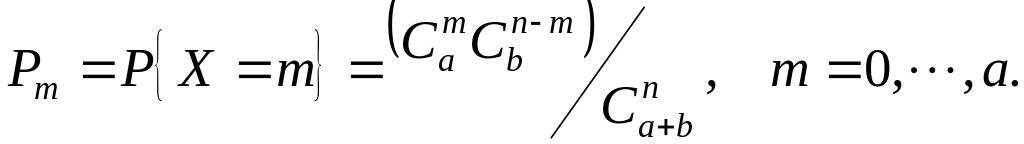
2. _{для непрерывной случайной величины: равномерный (плотность вероятности непрерывной постоянна на отрезке , а вне его равна нулю), показательный 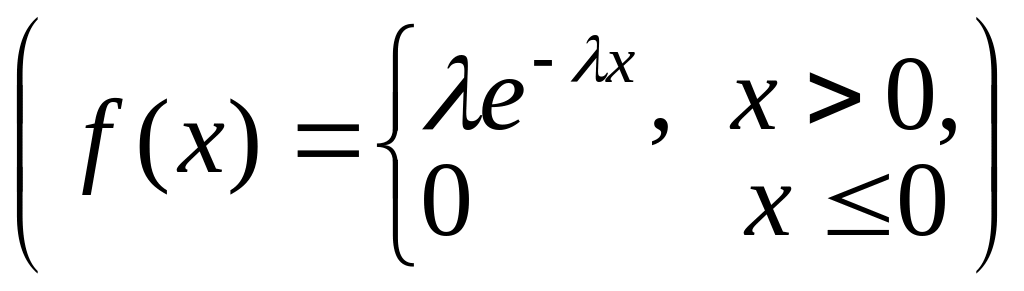, нормальный.}

Биномиальное распределение

Пусть производится независимых испытаний, в каждом из которых событие может появится или не появиться. Вероятность наступления события во всех испытаниях постоянна и равна (следовательно, вероятность непоявления ). В качестве дискретной случайной величины рассмотрим число появлений события в этих испытаниях. Закон распределения данной случайной величины называется биномиальным законом и имеет вид

				…		…
				…		…

Распределение Пуассона

Распределение Пуассона имеет вид

				…		…
				…		…

где .

Простейший поток событий

Рассмотрим события, которые наступают в случайные моменты времени.

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.

Потоки могут обладать свойствами стационарности, отсутствия последействия и ординарности.

Свойство стационарности характеризуется тем, что вероятность появления событий на любом промежутке времени зависит только от числа и от длительности промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися.

Свойство отсутствия последействия характеризуется тем, что вероятность появления событий на любом промежутке времени не от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка.

Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно.

Простейшим (пуассоновским) называют поток, который обладает свойствами стационарности, отсутствия последействия и ординарности.

Интенсивностью потока называют среднее число событий, которые появляются в единицу времени.

Если постоянная интенсивность потока известна, то вероятность появления событий простейшего потока за время длительностью определяется формулой Пуассона

.

(31)

Геометрическое распределение

Пусть производятся независимые испытания, в каждом из которых вероятность появления события равна и, следовательно, вероятность его непоявления . Испытания заканчиваются, как только появится событие . Таким образом, если событие появилось в м испытании, то в предыдущих испытаниях оно не появилось.

Через обозначим дискретную случайную величину – число испытаний, которое нужно провести до первого появления события .

Вероятность того, что в первых испытаниях событие не наступило, а в -м испытании появилось, равна

.

(32)

Геометрическое распределение имеет вид

			3	…		…
				…		…