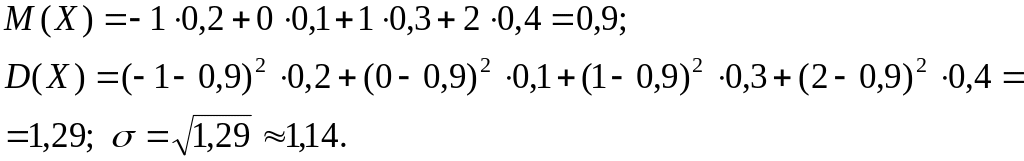- •4.7.2 Формула Пуассона.
- •4.7.3 Формулы Муавра-Лапласа.
- •4.7.4 Применение приближенных формул Пуассона и Муавра-Лапласа.
- •4.8 Случайные величины
- •4.9 Дискретные случайные величины
- •4.10 Функция распределения случайной величины. Плотность распределения непрерывной случайной величины.
- •4.11 Числовые характеристики случайной величины
- •4.12. Законы распределения дискретной случайной велисины
- •Биномиальное распределение
- •Распределение Пуассона
- •Простейший поток событий
- •Геометрическое распределение
- •Гипергеометрическое распределение
- •4.13 Законы распределения непрерывной случайной величины Равномерное распределение.
- •Нормальное распределение
- •Правило трех сигм.
4.10 Функция распределения случайной величины. Плотность распределения непрерывной случайной величины.
Наиболее
удобным способом задания закона
распределения случайной величины
(дискретной и непрерывной) является
аналитический способ. В этом случае
соответствие между значениями случайной
величины и их вероятностями задается
некоторой функцией
![]() .
Эта функция называется функцией
распределения случайной величины.
.
Эта функция называется функцией
распределения случайной величины.
Определение
18:
Функцией распределения
![]() (интегральной
функцией распределения) случайной
величины
называется
вероятность того, что она примет значение
меньшее, чем заданное
(интегральной
функцией распределения) случайной
величины
называется
вероятность того, что она примет значение
меньшее, чем заданное
![]() :
:
![]() .
.
Геометрический
смысл:
![]() есть вероятность того, что случайная
величина
примет значение, которое изображается
на числовой оси точкой, лежащей левее
точки
,
т.е. случайная величина попадет в интервал
есть вероятность того, что случайная
величина
примет значение, которое изображается
на числовой оси точкой, лежащей левее
точки
,
т.е. случайная величина попадет в интервал
![]()
Свойства функции распределения:
1°
![]() ;
;
2°
![]() ,
если
,
если
![]() (т. е. функция
(т. е. функция
![]() − функция неубывающая);
− функция неубывающая);
3°
Пусть
![]() и
и
![]() .
Так как событие
.
Так как событие
![]() является невозможным, а событие
является невозможным, а событие
![]() − достоверным, то
− достоверным, то
![]() ,
,
![]() ;
;
4°
вероятность попадания случайной величины
![]() в промежуток
в промежуток
![]()
![]()
Важнейшей характеристикой непрерывной случайной величины является плотность распределения вероятностей.
Плотностью
распределения вероятностей
![]() непрерывной
случайной величины
называется производная ее функции
распределения, т. е.
непрерывной
случайной величины
называется производная ее функции
распределения, т. е.
![]() .
Функцию
.
Функцию
![]() называют также дифференциальной функцией
распределения.
называют также дифференциальной функцией
распределения.
Свойства:
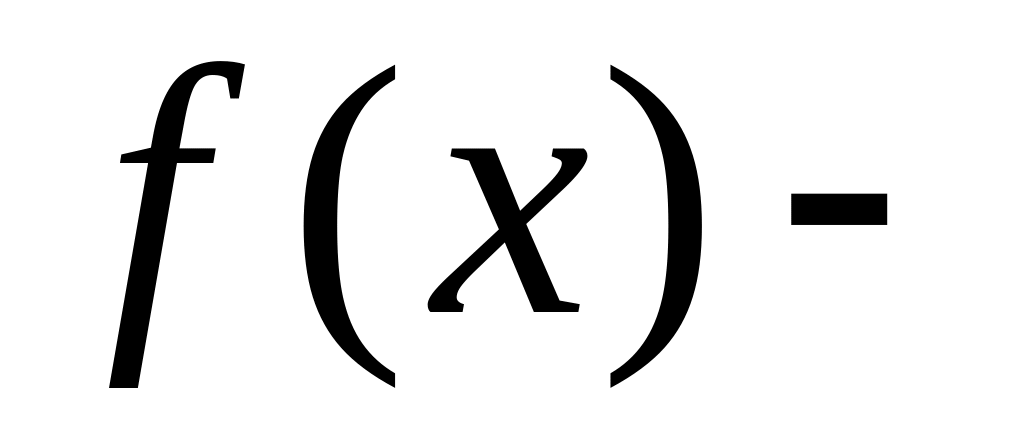 неотрицательная,
т.е.
неотрицательная,
т.е.
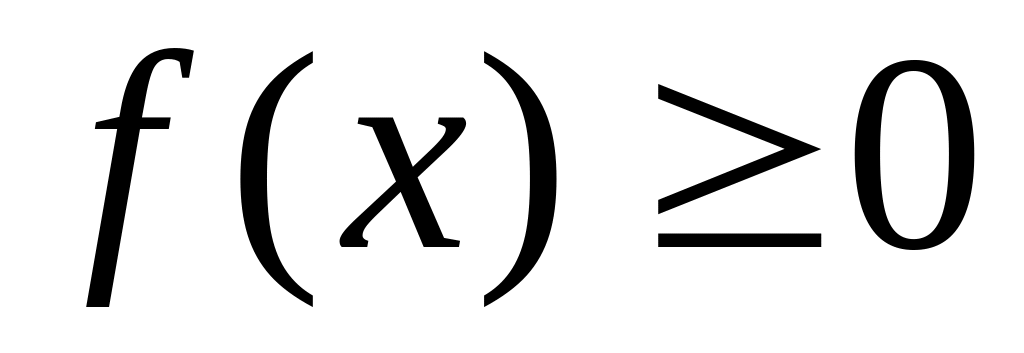 .
.Вероятность попадания непрерывной случайной величины в промежуток
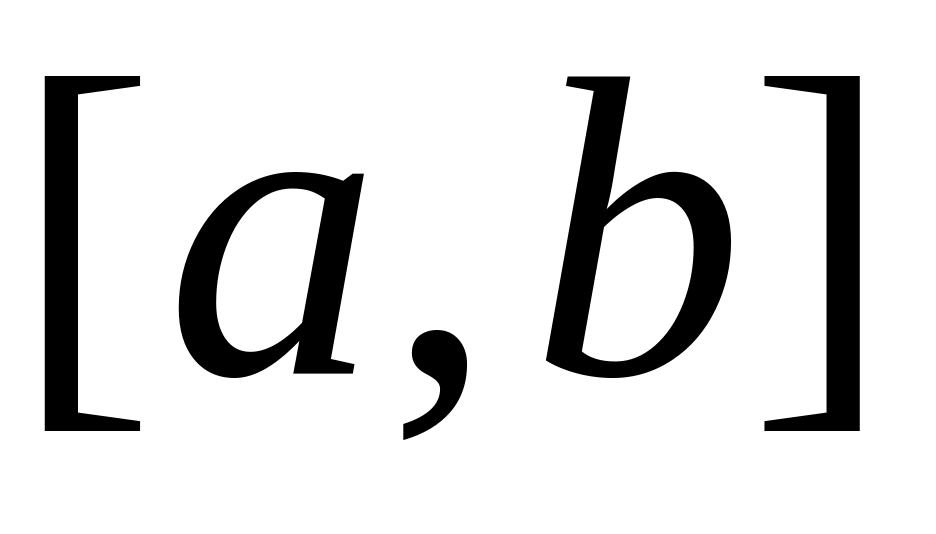 равна определенному интегралу от ее
плотности в пределах от
равна определенному интегралу от ее
плотности в пределах от
 до
до
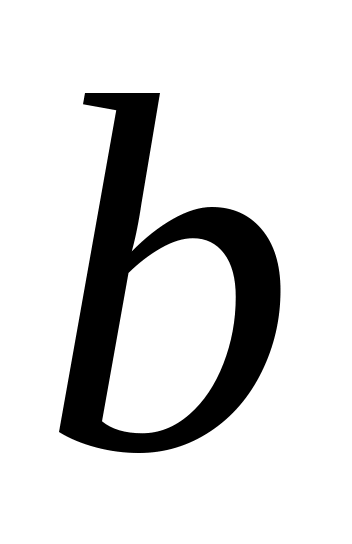 ,
т.е.
,
т.е.
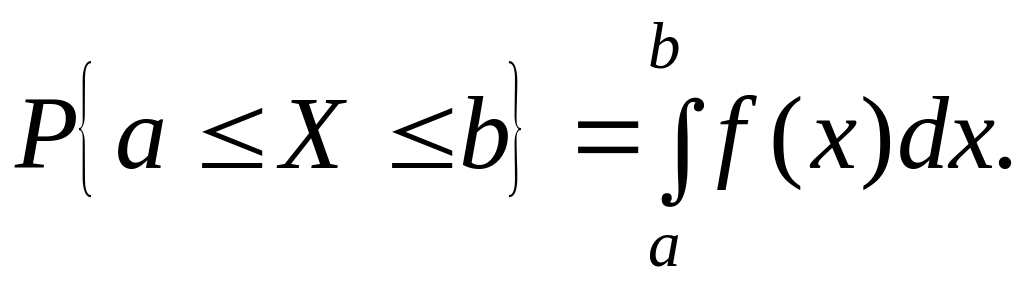
Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле
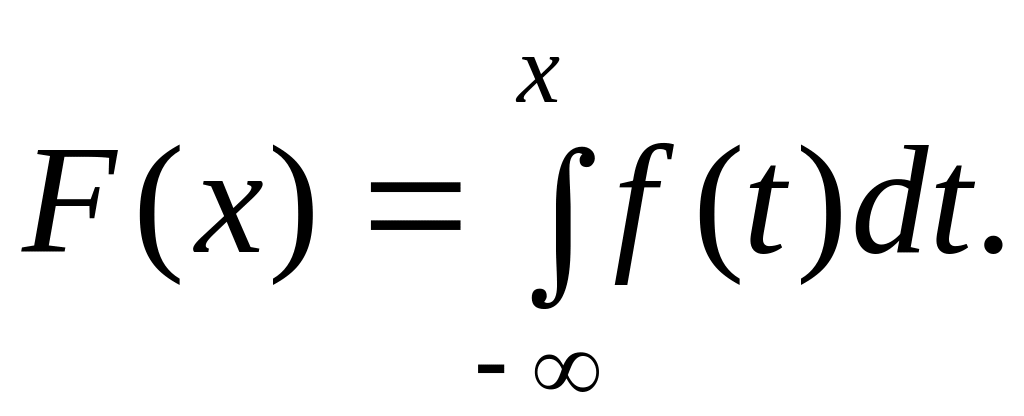
Условие нормировки: несобственный интеграл от плотности вероятности непрерывной случайной величины в бесконечных пределах равен единице, т.е.
4.11 Числовые характеристики случайной величины
Определение 19. Математическим ожиданием дискретной случайной величины называют сумму произведений всех возможных значений на их вероятности:
|
(25) |
или
|
(26) |
Ряд, стоящий в правой части (26) является сходящимся.
Определение 20. Математическим ожиданием непрерывной случайной величины называется интеграл
|
(27) |
Интеграл в правой части (27) предполагается абсолютно сходящимся.
Свойства математического ожидания:
1°
![]() ;
;
![]()
2°
![]() ;
;
3°
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий:
![]() ;
;
4°
Математическое ожидание отклонения
случайной величины от ее математического
ожидания равно нулю, т.е.
![]() .
.
5°
![]() .
.
Пример: В лотерее имеется 1000 билетов, из них выигрышных: 10 по 500 руб., 50 по 50 руб., 100 по 10 руб., 150 по 1 руб. Найти математическое ожидание выигрыша на один билет.
Решение:
Ряд распределения случайной величины
![]() суммы выигрыша на один билет
таков:
суммы выигрыша на один билет
таков:
-
X
500
50
10
1
0
P
0,01
0,05
0,1
0,15
0,69
Находим:
![]() руб.
руб.
Определение
21.
Пусть
− случайная величина и
![]() − ее математическое ожидание. Отклонением
случайной величины от ее математического
ожидания называют
разность между случайной величиной и
ее математическим ожиданием.
− ее математическое ожидание. Отклонением
случайной величины от ее математического
ожидания называют
разность между случайной величиной и
ее математическим ожиданием.
Теорема 6. Математическое ожидание отклонения равно нулю.
Определение 22. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
|
(28) |
Теорема 7. Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
|
(29) |
Для непрерывной случайной величины дисперсия определяется по формуле
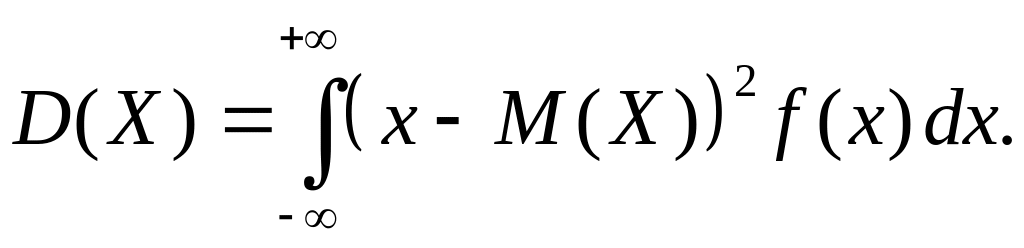 (30)
(30)
Свойства дисперсии:
1°
![]() ;
;
2°
![]() ;
;
3°
Дисперсия суммы двух независимых
случайных величин равна сумме дисперсий
этих величин:
![]() ;
;
4°
![]() .
.
Формулы (28), (29) можно переписать в виде, удобном для расчетов:
![]()
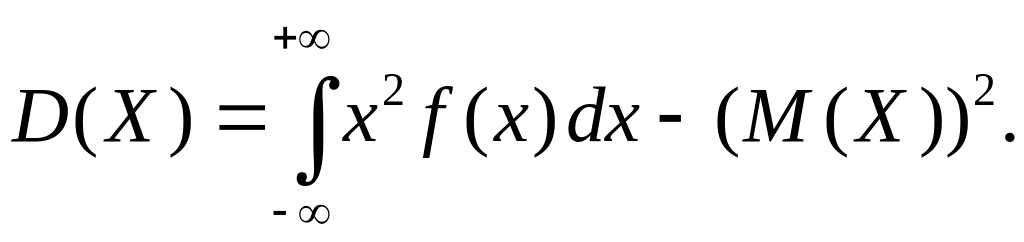
Определение 23. Средним квадратическим отклонением дискретной случайной величины называют корень квадратный из дисперсии:
|
(30) |
Пример: Дискретная случайная величина задана рядом распределения
-
X
-1
0
1
2
P
0,2
0,1
0,3
0,4