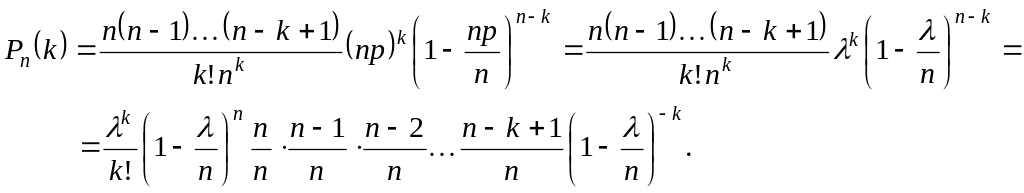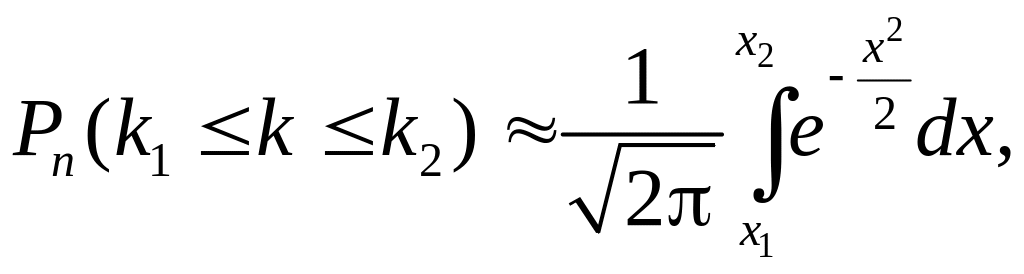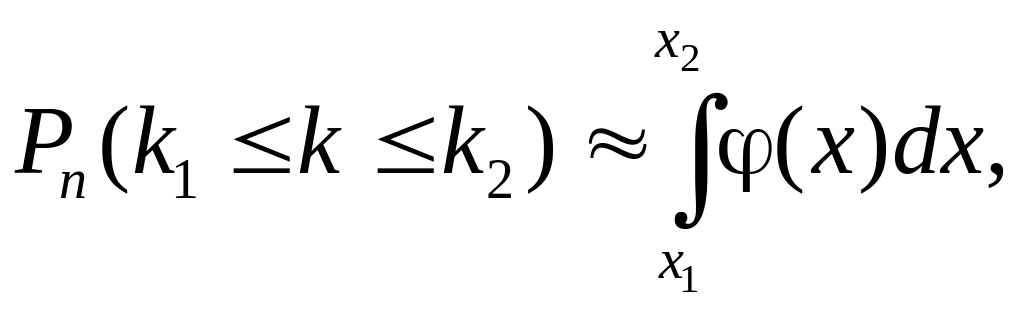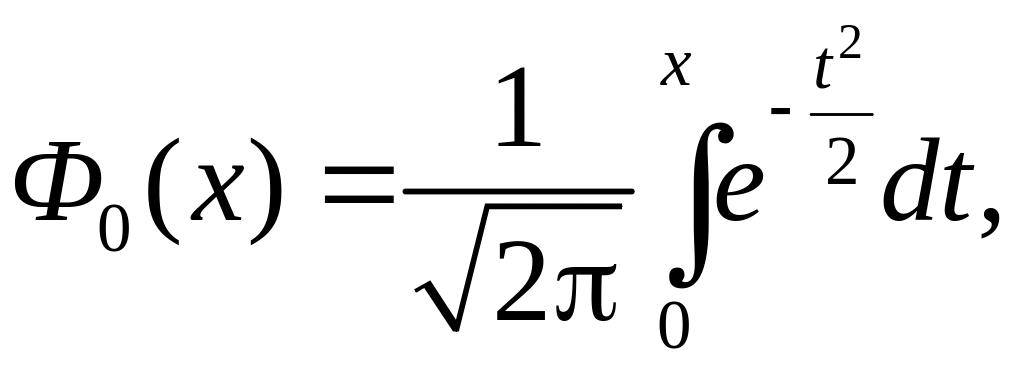14

4.7.2 Формула Пуассона.

Теорема 5 (Пуассона). Пусть число испытаний в схеме Бернулли велико , а вероятность успеха в одном испытании мала , причем мало также произведение . Тогда вероятность появления события раз в испытаниях вычисляется по формуле Пуассона

.

(20)

☺ Доказательство. Запишем формулу Бернулли

или с учетом обозначения ,

Так как при больших

Отсюда получаем формулу (20).☻

Пример: Телефонная станция обслуживает 1000 абонентов. В течение часа любой абонент независимо от остальных может сделать вызов с вероятностью 0,005. Требуется найти вероятность того, что в течение часа было не более 7 вызовов.

Решение: число вызовов. Нас интересуют значения Тогда

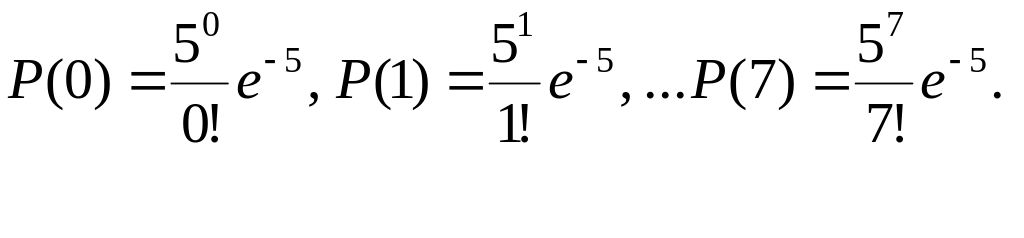
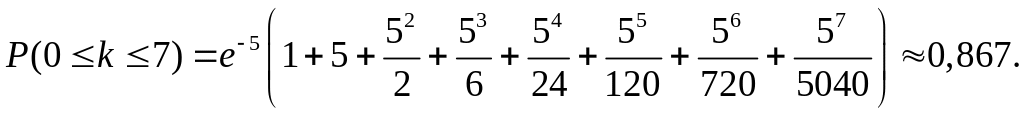
4.7.3 Формулы Муавра-Лапласа.

Локальная теорема Муавра-Лапласа. Если в схеме Бернулли число испытаний велико, вероятность не близка к нулю , то для всех справедлива приближенная формула (локальная формула Муавра-Лапласа)

,

(21)

где ,

.

(22)

Функция называется функцией Гаусса, а ее график  кривой вероятностей. Для функции Гаусса составлены таблицы значений (в «Приложениях»).

Пользуясь таблицей, следует учитывать, что:

а) функция четная, т.е. ;

б) при можно считать, что .

Пример: Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.

Решение: Здесь Применим формулу (15). Имеем: следовательно, Учитывая, что получаем

Интегральная теорема Муавра-Лапласа. Если в схеме Бернулли число велико, вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в пределах от до раз приближенно равна (интегральная формула Муавра-Лапласа)

(23)

Используя функцию Гаусса, равенство (23) можно переписать в виде:

Для упрощения вычислений при использовании формулы (23), вводят специальную функцию

называемую нормированной функцией Лапласа.

Равенство (23) можно переписать в виде

(24)

Наряду с нормированной функцией Лапласа используют функцию

.

Эта функция называется функцией Лапласа.

Свойства функции :

1. .

2. .

3. .

4. при

5.

Таблицы функций приводятся в большинстве учебников по теории вероятностей.

Пример: Проверкой установлено, что цех в среднем выпускает 96% продукции высшего сорта. На базе приемщик проверяет 200 изделий этого цеха. Если среди них окажется более 10 изделий не высшего сорта, то вся партия изделий бракуется, т.е. возвращается в цех. Какова вероятность того, что партия будет принята?

Решение: Здесь (вероятность негодного изделия), . Вероятность принятия всей партии находим по формуле (24): здесь .

Находим , ,

Заметим, что