6. Численное интегрирование обыкновенных дифференциальных уравнений методом Рунге-Кута

Такое интегрирование традиционно для МАТЛАБА, оно требует сначала создать файл-функцию, содержащий правую часть дифференциального уравнения, записанного в нормальной форме и начинающийся со слова function, затем файл-сценарий с указанием подынтегральной функции, интервала интегрирования и начальных условий. Кратко обозначив используемые здесь файлы как студенческие функцию и интеграл, приведем их, команду на интегрирование и результат его:

%studf

function xprime=studf(t,x);

xprime=-1.5*x;

%studint

[t,x]=ode45('studf',[0 5],[1]);

plot(t,x),grid

>> studint

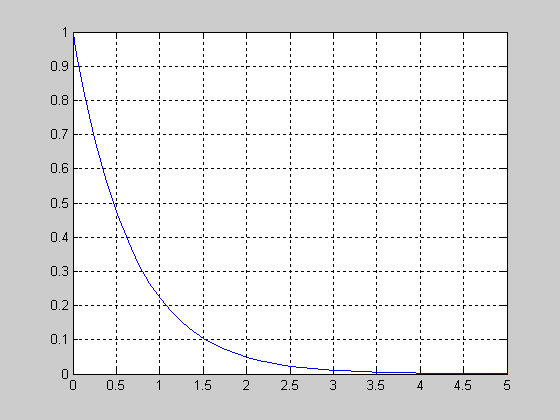
Очевидно, здесь при единичном начальном условии было проинтегрировано дифференциальное уравнение dx/dt=-1.5*x, и получена экспонента.

Литература (основная):

1. Дьяконов В.П. MATLAB 6/6.1/6.5+SIMULINK. Основы применения. Полное руководство пользователя. Москва: Солон-Пресс, 2002.