
- •«Нижегородский государственный архитектурно-строительный университет» (ннгасу)
- •1.2. Нагрузки и расчетный пролет
- •2. Расчет по предельным состояниям первой группы
- •2.1. Расчет на прочность по изгибающему моменту
- •2.3. Расчёт на прочность по поперечной силе.
- •3. Расчет по предельным состояниям второй группы
- •3.1. Геометрические характеристики
- •3.2. Определение потерь предварительного напряжения арматуры.
- •3.3. Проверка расчетного сечения на образование трещин
- •3.4. Расчет балки по раскрытию трещин
- •3.5. Определение прогиба балки
3.4. Расчет балки по раскрытию трещин
Ширина раскрытия нормальных трещин определяется по формуле:
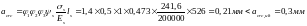
где
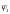 - коэффициент, учитывающий продолжительность
действия нагрузки, принимаемый равным
1,4 – при продолжительном действии
нагрузки;
- коэффициент, учитывающий продолжительность
действия нагрузки, принимаемый равным
1,4 – при продолжительном действии
нагрузки;
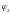 - коэффициент,
учитывающий профиль продольной арматуры,
принимаемый равным 0,5 – для арматуры
периодического профиля и канатной;
- коэффициент,
учитывающий профиль продольной арматуры,
принимаемый равным 0,5 – для арматуры
периодического профиля и канатной;
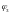 - коэффициент,
учитывающий характер нагружения,
принимаемый равным 1,0 – для изгибаемых
элементов;
- коэффициент,
учитывающий характер нагружения,
принимаемый равным 1,0 – для изгибаемых
элементов;
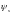 - коэффициент,
учитывающий неравномерное распределение
относительных деформаций растянутой
арматуры между трещинами определяется
по формуле:
- коэффициент,
учитывающий неравномерное распределение
относительных деформаций растянутой
арматуры между трещинами определяется
по формуле:
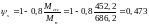
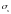 - напряжение в
продольной растянутой арматуре в
нормальном сечении с трещиной от
соответствующей внешней нагрузки,
определяемое по формуле:
- напряжение в
продольной растянутой арматуре в
нормальном сечении с трещиной от
соответствующей внешней нагрузки,
определяемое по формуле:
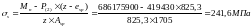
где
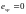 - расстояние от центра тяжести той же
арматуры Asp
до точки приложения усилия P(2)
- расстояние от центра тяжести той же
арматуры Asp
до точки приложения усилия P(2)
 -
расстояние от центра тяжести арматуры,
расположенной в растянутой зоне сечения,
до точки приложения равнодействующей
усилий в сжатой зоне балки; для элементов
двутаврового поперечного сечения
допускается значение z
принимать равным:
-
расстояние от центра тяжести арматуры,
расположенной в растянутой зоне сечения,
до точки приложения равнодействующей
усилий в сжатой зоне балки; для элементов
двутаврового поперечного сечения
допускается значение z
принимать равным:
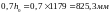 ;
;
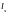 -
базовое (без учета влияния вида поверхности
арматуры) расстояние между смежными
нормальными трещинами, определяемое
по формуле:
-
базовое (без учета влияния вида поверхности
арматуры) расстояние между смежными
нормальными трещинами, определяемое
по формуле:
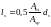 ,
,
где
 - площадь сечения растянутого бетона.
- площадь сечения растянутого бетона.
Для двутавровых сечений высота растянутой зоны бетона определяется по формуле:
 <
<
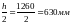 ,где
,где
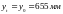 - высота растянутой
зоны бетона, определяемая как для
упругого материала;
- высота растянутой
зоны бетона, определяемая как для
упругого материала;
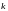 -
поправочный коэффициент, равный 0,95;
-
поправочный коэффициент, равный 0,95;
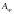 -
площадь сечения растянутой арматуры;
-
площадь сечения растянутой арматуры;
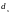 - номинальный
диаметр арматуры
- номинальный
диаметр арматуры


3.5. Определение прогиба балки
Заменяющий
момент
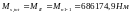 ,
так как равнодействующая усилий обжатия
сечения напряженной арматурой совпадает
с центром тяжести арматуры.
,
так как равнодействующая усилий обжатия
сечения напряженной арматурой совпадает
с центром тяжести арматуры.
Кривизна элемента:

где
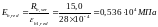
 равно, при
продолжительном действии и влажности
равно, при
продолжительном действии и влажности
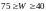 -
-
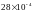
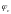 по таблице приложения
в зависимости от
по таблице приложения
в зависимости от
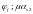 и
и
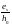 ;
;
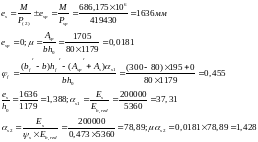
Откуда

Максимальный прогиб балки в середине пролета:
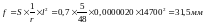 или
или
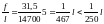
Здесь
S
– коэффициент, зависящий от расчетной
схемы элемента и вида нагрузки, при
действии равномерно распределенной
нагрузки значение
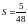 .
.
Запроектированная балка удовлетворяет требованиям I и II группы предельных состояний.

Рисунок 2 - К расчету балки по нормальному сечению на действие
поперечной силы
