Выбор типа приближения.
В данной задаче применяем диффузионное
приближение. Это приближение, которое
предполагает, что различные диффузионные
потоки действуют независимо друг от
друга (пренебрегаем перекрестными
членами вторых производных
).
Предположим, что все потоки в уравнениях (2.15) – (2.17) действуют независимо друг от друга ( ) (2.20), например, в задаче тепломассопереноса передача тепла условно не зависит от передачи массы. Это приводит к тому, что общую систему уравнений можно разделить на отдельные системы более низкого порядка и решать отдельные задачи. Задача упрощается за счет того, что обобщённые скорости потоков являются функциями только одной координаты, т.е. матрица коэффициентов Онсагера имеют линейную диагональную форму. В этом случае уравнения конвективного массопереноса представляют собой полилинейную форму, т.е. в декартовой системе координат Vx, Vy, Vz являются функцией только той координаты, по которой идет движение потока. В этом случае уравнение конвективного потока для скоростей по виду совпадает с уравнением переноса энергии.
(2.21)
Многие задачи механики (колебания струн, стержней, мембран и трехмерных объемов) и физики (электромагнитные колебания) описываются уравнением колебаний вида
(2.22)
где неизвестная функция и(х,t) зависит от п (п = 1,2,3) пространственных координат х = (x1, x2 ,….. ,хп) и времени t; коэффициенты , р и q определяются свойствами среды, где происходит колебательный процесс; свободный член F(x,t) выражает интенсивность внешнего возмущения (давление).
Постановка граничных условий.
Уравнение колебаний наклона измерительной оси:
=k
Перейдём в цилиндрическую систему координат:
Поставим граничные условия:
Жёсткое закрепление по плоскости ХОУ
Е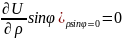
Е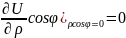
Е
Можем использовать точечный потенциал
Е(
Е(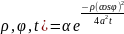
Выбор основного блока из пакета программ
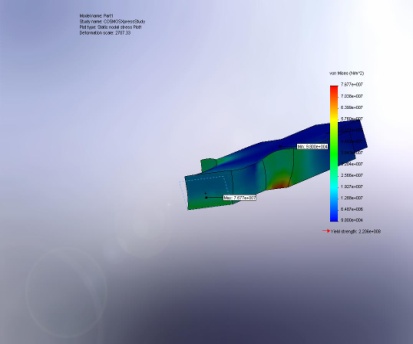
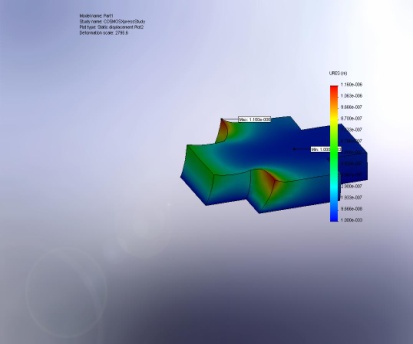
Данное приближение соответствует расчетам в пакете Cosmospress среды SolidWorks. Проведём несколько опытов, и выясним таким образов, как будет меняться погрешность в зависимости от силы действующей на датчик.
Опыт 1
No. |
Body Name |
Material |
Mass |
Volume |
1 |
Part1 |
[SW]Plain Carbon Steel |
0.026325 kg |
3.375e-006 m^3 |
Mesh Information |
|
Mesh Type: |
Solid Mesh |
Mesher Used: |
Standard |
Automatic Transition: |
Off |
Smooth Surface: |
On |
Jacobian Check: |
4 Points |
Element Size: |
1.5006 mm |
Tolerance: |
0.07503 mm |
Quality: |
High |
Number of elements: |
6778 |
Number of nodes: |
10779 |
Time to complete mesh(hh;mm;ss): |
00:00:01 |
Computer name: |
STUDENT-5 |
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot1 |
VON: von Mises Stress |
|
|
|
|
Part1-COSMOSXpressStudy-Stress-Plot1 |
||
JPEG |
||
|
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot2 |
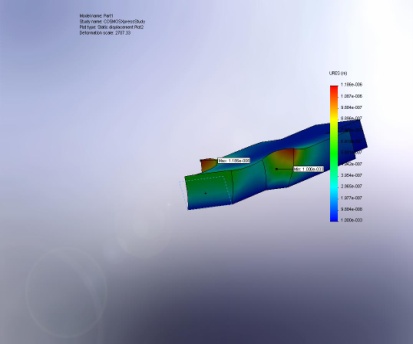
URES: Resultant Displacement |
|
|
|
|
Part1-COSMOSXpressStudy-Displacement-Plot2 |
||
JPEG |
||
|
Material name: |
[SW]Plain Carbon Steel |
Description: |
|
Material Source: |
Used SolidWorks material |
Material Library Name: |
|
Material Model Type: |
Linear Elastic Isotropic |
Property Name |
Value |
Units |
Elastic modulus |
2.1e+011 |
N/m^2 |
Poisson's ratio |
0.28 |
NA |
Mass density |
7800 |
kg/m^3 |
Yield strength |
2.2059e+008 |
N/m^2 |
Опыт 2
No. |
Body Name |
Material |
Mass |
Volume |
1 |
Part1 |
[SW]Plain Carbon Steel |
0.026325 kg |
3.375e-006 m^3 |
Mesh Information |
|
Mesh Type: |
Solid Mesh |
Mesher Used: |
Standard |
Automatic Transition: |
Off |
Smooth Surface: |
On |
Jacobian Check: |
4 Points |
Element Size: |
1.5006 mm |
Tolerance: |
0.07503 mm |
Quality: |
High |
Number of elements: |
6778 |
Number of nodes: |
10779 |
Time to complete mesh(hh;mm;ss): |
00:00:01 |
Computer name: |
STUDENT-5 |
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot1 |
VON: von Mises Stress |
|
|
|
|
Part1-COSMOSXpressStudy-Stress-Plot1 |
||
JPEG |
||
|
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot2 |
URES: Resultant Displacement |
|
|
|
|
Part1-COSMOSXpressStudy-Displacement-Plot2 |
||
JPEG |
||
|
Material name: |
[SW]Plain Carbon Steel |
Description: |
|
Material Source: |
Used SolidWorks material |
Material Library Name: |
|
Material Model Type: |
Linear Elastic Isotropic |
Property Name |
Value |
Units |
Elastic modulus |
2.1e+011 |
N/m^2 |
Poisson's ratio |
0.28 |
NA |
Mass density |
7800 |
kg/m^3 |
Yield strength |
2.2059e+008 |
N/m^2 |
Опыт 3
No. |
Body Name |
Material |
Mass |
Volume |
1 |
Part1 |
[SW]Cast Carbon Steel |
0.026325 kg |
3.375e-006 m^3 |
Mesh Information |
|
Mesh Type: |
Solid Mesh |
Mesher Used: |
Standard |
Automatic Transition: |
Off |
Smooth Surface: |
On |
Jacobian Check: |
4 Points |
Element Size: |
1.5006 mm |
Tolerance: |
0.075032 mm |
Quality: |
High |
Number of elements: |
6778 |
Number of nodes: |
10779 |
Time to complete mesh(hh;mm;ss): |
00:00:01 |
Computer name: |
STUDENT-5 |
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot1 |
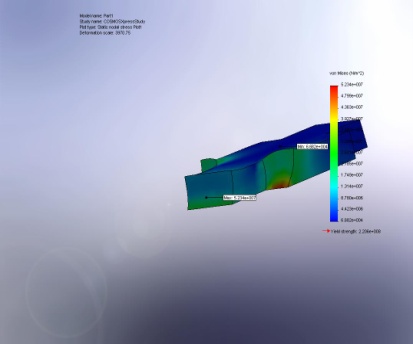
VON: von Mises Stress |
|
|
|
|
Part1-COSMOSXpressStudy-Stress-Plot1 |
||
JPEG |
||
|
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot2 |
URES: Resultant Displacement |
|
|
|
|
Part1-COSMOSXpressStudy-Displacement-Plot2 |
||
JPEG |
||
|
Property Name |
Value |
Units |
Elastic modulus |
2e+011 |
N/m^2 |
Poisson's ratio |
0.32 |
NA |
Mass density |
7800 |
kg/m^3 |
Yield strength |
2.4817e+008 |
N/m^2 |
Опыт 4
No. |
Body Name |
Material |
Mass |
Volume |
1 |
Part1 |
[SW]Cast Carbon Steel |
0.026325 kg |
3.375e-006 m^3 |
Mesh Information |
|
Mesh Type: |
Solid Mesh |
Mesher Used: |
Standard |
Automatic Transition: |
Off |
Smooth Surface: |
On |
Jacobian Check: |
4 Points |
Element Size: |
1.5006 mm |
Tolerance: |
0.075032 mm |
Quality: |
High |
Number of elements: |
6778 |
Number of nodes: |
10779 |
Time to complete mesh(hh;mm;ss): |
00:00:01 |
Computer name: |
STUDENT-5 |
Solver Information |
|
Quality: |
High |
Solver Type: |
Automatic |
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot1 |
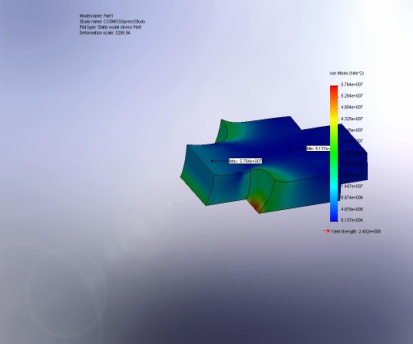
VON: von Mises Stress |
|
|
|
|
Part1-COSMOSXpressStudy-Stress-Plot1 |
||
JPEG |
||
|
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot2 |
URES: Resultant Displacement |
|
|
|
|
Part1-COSMOSXpressStudy-Displacement-Plot2 |
||
JPEG |
||
|
Material name: |
[SW]Cast Carbon Steel |
Description: |
|
Material Source: |
Used SolidWorks material |
Material Library Name: |
|
Material Model Type: |
Linear Elastic Isotropic |
Property Name |
Value |
Units |
Elastic modulus |
2e+011 |
N/m^2 |
Poisson's ratio |
0.32 |
NA |
Mass density |
7800 |
kg/m^3 |
Yield strength |
2.4817e+008 |
N/m^2 |
Опыт 5
No. |
Body Name |
Material |
Mass |
Volume |
1 |
Part1 |
[SW]Cast Carbon Steel |
0.026325 kg |
3.375e-006 m^3 |
Mesh Information |
|
Mesh Type: |
Solid Mesh |
Mesher Used: |
Standard |
Automatic Transition: |
Off |
Smooth Surface: |
On |
Jacobian Check: |
4 Points |
Element Size: |
1.5006 mm |
Tolerance: |
0.075032 mm |
Quality: |
High |
Number of elements: |
6778 |
Number of nodes: |
10779 |
Time to complete mesh(hh;mm;ss): |
00:00:01 |
Computer name: |
STUDENT-5 |
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot1 |
VON: von Mises Stress |
|
|
|
|
Part1-COSMOSXpressStudy-Stress-Plot1 |
||
JPEG |
||
|
Name |
Type |
Min |
Location |
Max |
Location |
||||||||||
Plot2 |
URES: Resultant Displacement |
|
|
|
|
Part1-COSMOSXpressStudy-Displacement-Plot2 |
||
JPEG |
||
|
Material name: |
[SW]Cast Carbon Steel |
Description: |
|
Material Source: |
Used SolidWorks material |
Material Library Name: |
|
Material Model Type: |
Linear Elastic Isotropic |
Property Name |
Value |
Units |
Elastic modulus |
2e+011 |
N/m^2 |
Poisson's ratio |
0.32 |
NA |
Mass density |
7800 |
kg/m^3 |
Yield strength |
2.4817e+008 |
N/m^2 |