
Московский Государственный Университет Инженерной Экологии
Кафедра «Сопротивление материалов и прочность конструкций»
Курсовая работа по дисциплине:
«Прочность машин и аппаратов» на тему:
«Расчет тонкостенных корпусов сосудов и аппаратов»
Вариант №
Выполнил:
Проверил преподаватель: Скачков Ю.А.
Москва 2012г.
ОБОЗНАЧЕНИЯ:
![]() ,
,![]() — главные радиусы кривизны, мм;
— главные радиусы кривизны, мм;
R - радиус срединной поверхности сферической оболочки;
r— радиус параллельного круга, мм;
h— толщина оболочки, мм;
m — моментная нагрузка, равномерно распределенная по окружности, Н*мм/мм;
Р— радиальная нагрузка, равномерно распределенная по окружности, Н/мм;
q — распределенная по площади нагрузка (давление), МПа;
Ns — нормальное меридиональное усилие, Н/мм;
Nt — нормальное кольцевое усилие, Н/мм;
Ms — меридиональный изгибающий момент, Н*мм/мм;
Mt — кольцевой изгибающий момент, Н*мм/мм;
![]() — поперечное усилие, Н/мм;
— поперечное усилие, Н/мм;
σs— нормальное меридиональное напряжение, МПа;
σt — кольцевое меридиональное напряжение, МПа;
Δ — радиальное перемещение, мм;
υ — угол поворота нормали к срединной поверхности оболочки, рад;
![]() —
нормальные
меридиональные и кольцевые напряжения,
вычисленные по
—
нормальные
меридиональные и кольцевые напряжения,
вычисленные по
безмоментной теории, МПа;
![]() —
радиальное
и угловое перемещения на краю оболочки,
вычисленные по
—
радиальное
и угловое перемещения на краю оболочки,
вычисленные по
безмоментной теории;
Pz — осевая равнодействующая внешней нагрузки на оболочку, Н;
Е — модуль упругости материала оболочки, МПа;
μ — коэффициент Пуассона материала оболочки.
Выполним расчет сосуда, состоящего из участков сферической, цилиндрической и конической оболочек:
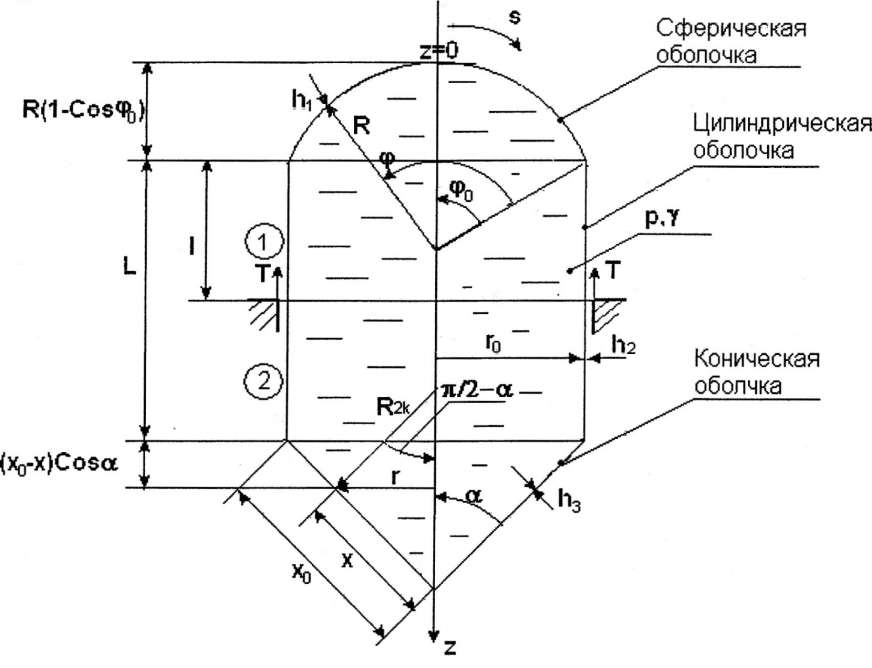
Исходные данные:
Η=2500 мм
r=2000 мм
h1=14 мм
h2=10 мм
h3 = 14 мм
q = 0.2 МПа
φ0= 30°
α = 45°
Механические характеристики конструкционного материала:
•
модуль
упругости Ε = 2* ![]() МПа
МПа
• коэффициент Пуассона μ=0.3
![]() 220
МПа
220
МПа
1. Проверочный расчет узлов сопряжения
1.1 Расчет узла сопряжения цилиндрической и сферической оболочки
Для решения узла сопряжения применяем метод сил. В соответствии с этим методом разрезаем (мысленно) оболочки и заменяем их действия друг на друга силами и моментами.
 Определение
неизвестных усилий
Определение
неизвестных усилий
![]()
Составим уравнение равновесия сферической оболочки в проекциях на ось z:
![]()
Откуда находим
![]()
По
правилу параллелограмма разложим силу
![]() на
на
![]() и
и
![]() :
:
![]()
![]()
3) Радиальное усилие P и момент m определяем из условия
совместной работы цилиндрической и сферической оболочек, полагая равными нулю относительные радиальное и угловое перемещения их крайних сечений:
![]()
Это означает, что радиальное перемещение крайнего сечения сферической оболочки и цилиндрического корпуса должны быть равны, и угол поворота крайнего сечения сферической оболочки должен быть равен углу поворота крайнего сечения цилиндрической оболочки, т.е.
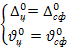
Воспользовавшись принципом независимости действия сил, из данных условий получаем следующие соотношения:
(1)![]()
![]()
![]()
где
индексами ![]() ,
,
![]() и
m
обозначены перемещения крайних сечений
цилиндрической и сферической оболочек
соответственно от краевых радиальных
усилий и краевого момента, значком "
* " помечены перемещения от безмоментных
составляющих нагрузки, т.е. от
и
m
обозначены перемещения крайних сечений
цилиндрической и сферической оболочек
соответственно от краевых радиальных
усилий и краевого момента, значком "
* " помечены перемещения от безмоментных
составляющих нагрузки, т.е. от ![]() и
q
-
для сферической оболочки; от Nz
и
q
-
для цилиндрической оболочки.
и
q
-
для сферической оболочки; от Nz
и
q
-
для цилиндрической оболочки.
Для применения данной теории необходимо убедиться, что все рассматриваемые оболочки являются длинными. Для этого необходимо, чтобы длины зон краевого эффекта удовлетворяли следующим условиям:
-
для
цилиндра
![]() ,
,
-
для
сферы
![]() .
.
Подставляя в систему (1) выражения для перемещений крайних сечений оболочек, получим систему линейных алгебраических уравнений относительно неизвестных Риm:
 (2)
(2)
 где
где
![]()
![]()
![]()
![]()
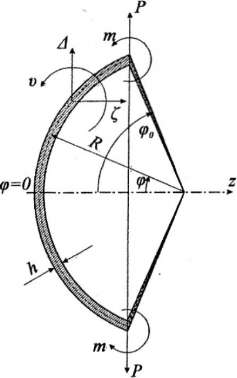
Определяем безмоментные составляющие в системе уравнений (2).
Уравнение равновесия для сферической оболочки:
![]()
т.к.
![]() и
и ![]() то
то
![]()
Т.
к. для сферической оболочки ![]() ,
то из уравнения Лапласа
,
то из уравнения Лапласа
![]()
![]() найдем
найдем
![]() =
=![]()
 тогда
тогда

По
безмоментной теории найдем
![]() .
.
![]()
![]()
Так
как для цилиндрической оболочки ![]() ,
,
![]() , то из уравнения Лапласа
, то из уравнения Лапласа ![]() получим:
получим:
![]()
Тогда
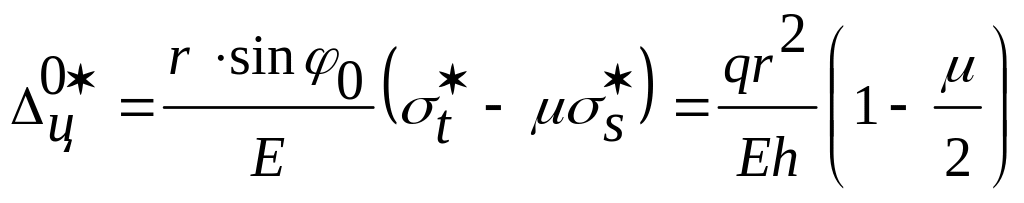
Т.к.
q=const
(увеличивается только r)
то ![]() ,
а
,
а ![]() можно пренебречь из-за его малости.
можно пренебречь из-за его малости.
Таким образом, у нас есть все необходимые данные, для решения системы (2).
Определяем теперь внутренние усилия и перемещения в элементах рассматриваемого узла.
Т.к. q=const (увеличивается только r) то , а можно пренебречь из-за его малости.
Таким образом, у нас есть все необходимые данные, для решения системы (2).
Решая систему (2) определяем m и P.
Определяем теперь внутренние усилия и перемещения в элементах рассматриваемого узла.
Расчет цилиндрической оболочки
Меридиональный изгибающий момент
![]() (3)
(3)
Нормальное кольцевое усилие
![]() (4)
(4)
Радиальное перемещение
(5)
Угол
поворота нормали к срединной поверхности
![]() (6)
(6)
Вычисления
по формулам 3-6 выполняем для ряда значений
аргумента ξ в интервале 0 < ξ < 3.2 с
шагом![]() .
.
Значения
безмоментных составляющих нормального
кольцевого усилия
![]() и радиального перемещения
и радиального перемещения ![]() заимствуем
из решения задачи по безмоментной теории
заимствуем
из решения задачи по безмоментной теории
Результата расчета цилиндрической оболочки сводим в табл. 1.
Таблица 1.
