Преобразование Фурье и его свойства Преобразование Фурье

Итак, преобразование Фурье бывает двух видов: дискретное и непрерывное. Непрерывное используется математиками в аналитических исследованиях, дискретное применяется во всех остальных случаях.

Непрерывное преобразование Фурье - преобразование, которое применяется к функции h(t), заданной на интервале  . В результате получается функция H(f):

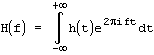
также существует обратное преобразование, которое позволяет по образу H(f) восстановить исходную функцию h(t):

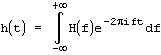
Очевидно, что образ H(f) является комплексной функцией вещественного аргумента, но также и h(t) может принимать не только вещественные, но и комплексные значения.

Применение преобразования Фурье является столь обширной темой, что этот вопрос не будет подниматься в этой статье. Можно только перечислить несколько областей: анализ сигналов, фильтрация, ускоренное вычисление корелляции и свертки, использование в алгоритмах быстрого умножения чисел, и во многих других случаях оно также находит свое применение.

19.

Дискретное косинусное преобразование (англ. Discrete Cosine Transform, DCT) — одно из ортогональных преобразований. Вариант косинусного преобразования для вектора действительных чисел. Применяется в алгоритмах сжатия информации с потерями, например, MPEG и JPEG. Это преобразование тесно связано с Дискретным преобразованием Фурье и является гомоморфизмом его векторного пространства.

Математически преобразование можно осуществить умножением вектора на матрицу преобразования. При этом матрица обратного преобразования с точностью до множителя равнатранспонированной матрице. В математике матрицы выбирают так, чтобы преобразование было ортонормированным, а постоянный множитель равен единице. В компьютерных приложениях это не всегда так.

Различные периодические продолжения сигнала ведут к различным типам ДКП. Ниже приводятся матрицы для первых четырёх типов ДКП:

Именно   чаще всего встречается в практических приложениях благодаря свойству «уплотнения энергии».

 для вектора из 8 чисел часто называют  . Наиболее распространён двумерный вариант преобразования для матриц 8x8, состоящий из последовательности  сначала для каждой строки, а затем для каждого столбца матрицы.

Существуют алгоритмы быстрого  -преобразования, похожие на алгоритм быстрого преобразования Фурье. Для   и других вариантов   с фиксированной размерностью вектора существуют также алгоритмы, позволяющие свести количество операций умножения к минимуму.

Существуют аналоги  , приближающие косинус числами, легко получающимися путём небольшого количества операций сдвига и сложения, что позволяет избежать операций умножения и тем самым повысить эффективность вычислений. Преимущество таких аналогов — более высокая скорость.

20.

Преобразование Уолша-Адамара

Существуют различные способы определения функций Уолша. Рассмотрим способ, основанный на взаимосвязи функций Уолша с функциями Радемахера. Последние определяются так:

где   – безразмерное время ( ), k є N – порядок (номер) функции,

Система функций Радемахера ортонормированна на интервале (0,1), то есть

однако неполна.

Функции Уолша, образующие полную ортонормированную систему, теперь можно определить так:

(5)

где «(+)» – сложение по модулю 2; w – порядок (номер) функции; n=log₂ N, где N=2ⁿ – количество функций системы; w_i – i-тый разряд двоичного представления порядка функции w (отсчёт слева, начиная с 0).

Функции Уолша могут служить базисом для спектрального представления сигнала, то есть любую интегрируемую на интервале   функцию можно представить рядом по системе функций Уолша:

с коэффициентами

Способ нумерации функций в системе называется упорядочением. Функции Уолша, сформированные в соответствии с выражением (5), упорядочены по Уолшу. На практике также применяетсяупорядочение по Адамару (had(h,Эта)) и по Пэли (pal(p,Эта)).

Функции had(h,Эта) можно сформировать с помощью матрицы Адамара. Матрицей Адамара H_N порядка N=2ⁿ, n є N называется квадратная матрица размера N x N с элементами +1 такая, что

H_N x H_N^T = N x E,

где H_N^T – транспонированная матрица, E – единичная матрица; при этом H₁=1.

Матрицу Адамара легко построить рекурсивно, так как:

Функция Уолша, упорядоченная по Адамару (had(h,Эта)) с номером h, является последовательностью прямоугольных импульсов длительностью 1/N от интервала (0,1) с единичными амплитудами и полярностями, соответствующими знакам элементов h-той строки матрицы Адамара.

Для цифрового анализа сигнала используются дискретные функции Уолша, которые являются отсчётами соответствующих непрерывных функций. Каждый отсчёт расположен в середине связанного с ним элемента непрерывной функции длительностью 1/N от интервала (0,1). Дискретные функции Уолша, упорядоченные по Уолшу, можно определить так:

где x_k – k-тый разряд в представлении номера отсчёта x в двоичной системе счисления:

Другой формой представления дискретных функций Уолша является матрица Адамара, номера столбцов которой соответствуют номерам дискретных значений (отсчётов) функций Уолша, а номера строк – номерам функций Уолша.