4. Лінійні неоднорідні системи диференціальних рівнянь

Нехай є система лінійних неоднорідних диференціальних рівнянь зі сталими коефіцієнтами

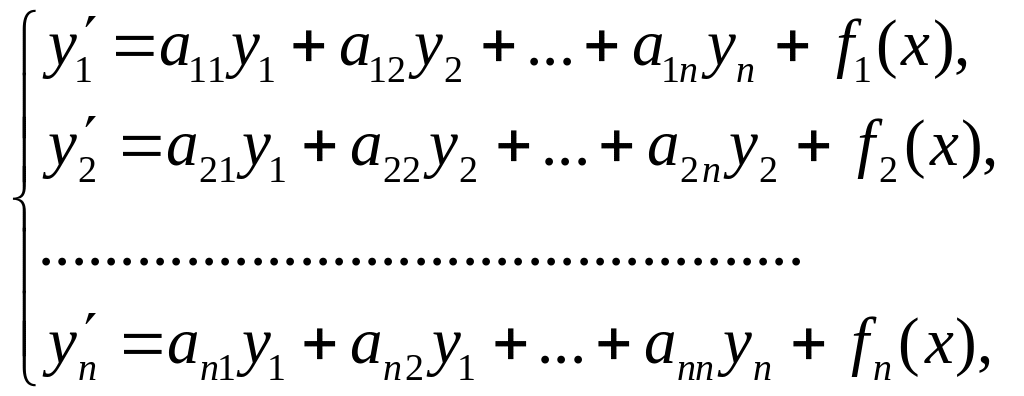(4.1)

у якій функції неперервні на проміжку . Запишемо її у векторно-матричному вигляді

, (4.2)

де вектор-функція своїми координатами має функції .

Теорема 4.1. (про структуру загального розв’язку). Загальний розв’язок неоднорідної системи (4.2) дорівнює сумі частинного розв’язку цієї системи і загального розв’язку відповідної однорідної системи

. (4.3)

Д о в е д е н н я. Нехай – частинний розв’язок ЛНС, – фундаментальна матриця розв’язків ЛОС (4.3). Спочатку доведемо, що вектор-функція є розв’язком ЛНС. Для цього підставимо вектор-функцію і її похідну у систему (4.2):

Ця рівність виконується для всіх з проміжку , бо , а . Отже, – розв’язок ЛНС.

Нехай – довільне число з інтервалу , – довільний сталий -вимірний вектор. Визначимо вектор так, щоб виконувалася рівність

.

Оскільки фундаментальна матриця розв’язків неособлива на проміжку , то вона на ньому має обернену . Тому . Не складно переконатися, що вектор-функція

задовольняє початкову умову .

Отже, вектор-функція є загальним розв’язком ЛНС.

5. Частинні розв’язки лінійних неоднорідних систем

Загальним способом побудови частинних розв’язків ЛНС є метод Лагранжа або по-іншому – метод варіації довільних сталих. В окремих випадках частинні розв’язки можна будувати методом невизначених коефіцієнтів.

1. Метод Лагранжа. За методом Лагранжа частинний розв’язок ЛНС

(5.1)

шукається у вигляді

,

де – фундаментальна матриця розв’язків відповідної ЛОС, – невідома вектор-функція, яку треба визначити так, щоб вектор-функція задовольняла ЛНС:

.

Інтегруючи здобуту рівність , дістаємо вектор-функцію :

.

(Інтегралом від вектор-функції називається вектор-функція, координатами якої є інтеграли від відповідних координат даної вектор-функції – щоб проінтегрувати вектор-функцію треба проінтегрувати її координати).

Отже, частинний розв’язок ЛНС можна знайти за формулою

.

Побудова частинного розв’язку ЛНС методом варіації довільних сталих здійснюється за такою схемою.

1. Будується фундаментальна матриця розв’язків відповідної ЛОС.

2. Для ЛОС складається загальний розв’язок , де довільний сталий вектор.

3. Частинний розв’язок шукається у вигляді , де – невідомий вектор, похідна якого визначається рівністю

і знаходиться за формулою . Тому

Загальний розв’язок ЛНС будується за формулою

.

Приклад 4. Знайти загальний розв’язок системи

Р о з в ’ я з а н н я. Фундаментальна матриця розв’язків відповідної однорідної системи побудована при розв’язувані прикладу 1:

.

Для реалізації описаного алгоритму побудови частинного розв’язку побудуємо матрицю , обернену фундаментальній:

(Якщо 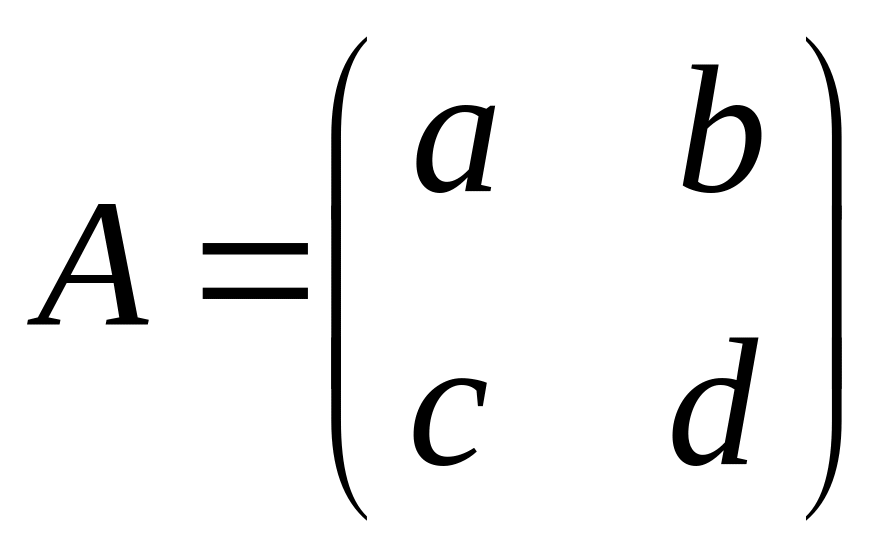– неособлива матриця, то ).

Визначимо вектор-функцію з рівності :

Побудуємо частинний розв’язок системи:

Складаємо загальний розв’язок даної системи

.

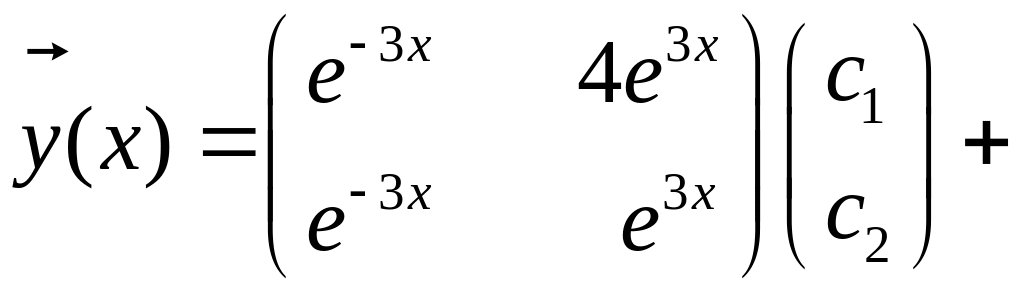
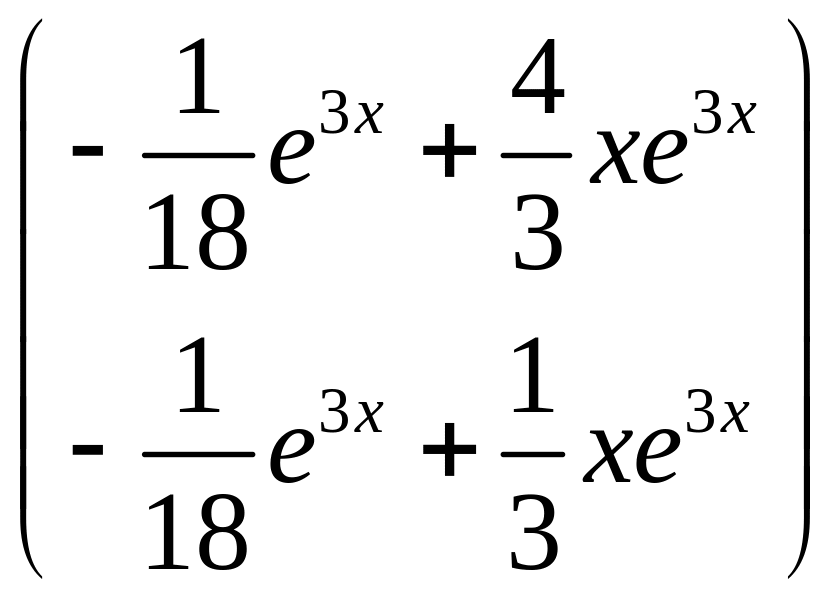Відповідь:

2. Метод невизначених коефіцієнтів. У випадках, коли вектор-функція має спеціальний вигляд, а саме:

1) ,

2) ,

частинні розв’язки ЛНС можна будувати методом невизначених коефіцієнтів.

Розглянемо перший випадок. Нехай , де – дійсне число, – векторний поліном

,

коефіцієнтами якого є - вимірні вектори . Залежно від числа розглядають два випадки:

– нерезонансний – не є коренем характеристичного рівняння;

– резонансний – є коренем характеристичного рівняння.

У нерезонансному випадку частинний розв’язок завжди можна знайти у вигляді

,

де - вимірні вектори визначаються з системи векторних рівнянь

,

,

…………………………..

,

,

.

Цю систему дістаємо, підставивши вектор-функцію та її похідну у ЛНС:

=

= ,

і прирівнюючи коефіцієнти при однакових степенях змінної :

,

= ,

………………………………

,

,

.

У резонансному випадку частинний розв’язок будується у вигляді

,

де – кратність числа як кореня характеристичного рівняння, а вектори визначаються як і в нерезонансному випадку.

Побудову частинного розв’язку ЛНС у випадку, коли

,

пропонуємо розглянути самостійно. Алгоритм побудови описано в підручнику Самойленко А.М., Перестюк М.О., Парасюк І.О. Диференціальні рівняння К.: Либідь, 2003. – 600 с. (Див. п. 2.4.5, с. 247).

Побудуємо методом невизначених коефіцієнтів частинний розв’язок системи (приклад 4)

Для цього запишемо систему у векторно-матричному вигляді

, (5.1)

де

.

Власними числами матриці є числа (Див. приклад 1). Оскільки коефіцієнт є простим власним значення матриці , то частинний розв’язок шукаємо у вигляді

де .

Підставимо вектор-функцію і її похідну в рівняння (5.1):

(5.2)

Розв’яжемо перше рівняння системи (5.2).

.

З другого рівняння дістаємо :

(5.3)

Система (5.3) матиме розв’язки тільки тоді, коли праві частини її рівнянь будуть однаковими. Тому . Візьмемо . Тоді .

Підсумовуючи зроблене, маємо

Примітка. Частинний розв’язок ЛНС, побудований методом невизначених коефіцієнтів збігається з частинним розв’язком, побудованим методом Лагранжа. Однак цього б не сталося, якби за координату взяли інше число.

17