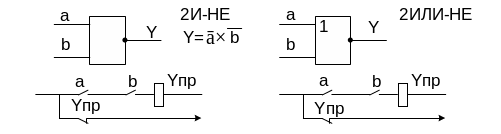Цифровые интегральные микросхемы
Общие понятия
Цифровые микросхемы, к которым относят логические элементы, триггеры, счетчики, шифраторы, микропроцессоры и т.д., работают с входными и выходными сигналами, принимающими дискретные значения (логический ноль или логическая единица).
Анализ и синтез цифровых схем проводится на основе Булевой алгебры. Цифровые схемы и Булевая алгебра оперируют логическими переменными, которые могут принимать два значения (логический ноль и логическая единица).
Основные действия над переменными:
- операция логического сложения (дизъюнкция) «ИЛИ» (+)
- логическое умножение (конъюнкция) «И» (х)
- инверсия (отрицание)
«НЕ» (![]() )
)
Логическим законам и действиям могут быть сопоставлены эквивалентные схемы в релейном виде.
«ИЛИ» у=х1+х2

Соответствует параллельному включению контактов. Для получения сигнала У необходимо замкнуть х1 или х2.
«И» у=х1×х2
![]()
Для получения единицы У на выходе необходимо замкнуть х1, и х2.
«НЕ» у=
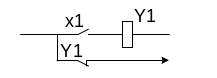
Основные свойства логических функций:
свойство сложения
0+0=0
х=0 контакт разомкнут, х=1 контакт замкнут
0+1=1
1+1=1
свойство логического умножения
0×0=0
0×1=0
1×1=1
свойство отрицания
![]() =1
=1
![]() =0
=0
=1
=0
Приведенные соотношения – аксиомы. Основные свойства в общем виде:
а+0=а
0+1=1
а+а=а
ā+а=1
а×0=0
а×1=а
ā×а=0
а×а=а
ā=а
Основные логические законы:
переместительный
a+b=b+a
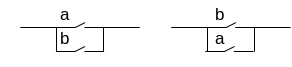
сочетательный
(a+b)+c=a+(b+c)
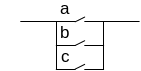
(a×b) ×c=a×(b×c)
![]()
распределительный
a×(b+c)=a×b+a×c
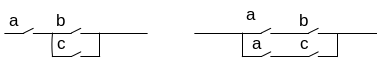
a+b×c=(a+b) ×(a+c)

закон поглощения
a+ab=a(1+b)=a
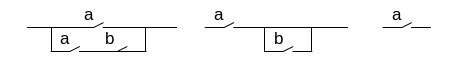
a(a+b)=a+ab=a
![]()
закон склеивания
ab+a![]() =a
=a
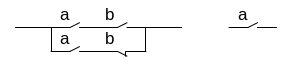
(a+b)(a+ )=a

законы отрицания (законы Моргана)
И ↔ ИЛИ
ā+ = ā×
ā× = ā+
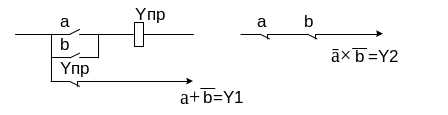
2n, где n – количество операндов
а 0 0 1 1
b 0 1 0 1
Yпр 0 1 1 1
Y1 1 0 0 0
Y2 1 0 0 0
При анализе цепи с выходным сигналом Y2 рассуждаем так:
при а=0 нормально замкнутый контакт в схеме в замкнутом состоянии, т.к. его катушка (не показана на схеме) обесточена.
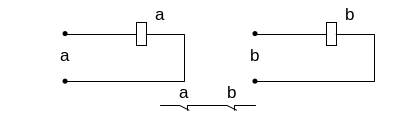
Т.к. при любых комбинациях входных операндов а и b Y1=Y2, то эти две схемы абсолютно адекватны друг с другом с точки зрения реализации ими логических функций.
Подобным образом может быть проверено любое выражение, написанное в разделе «Основные логические функции».
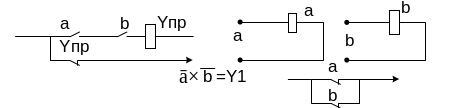
а 0 0 1 1 подобная таблица – таблица истинности
b 0 1 0 1
Yпр 0 1 1 1
Y1 1 0 0 0
Y2 1 0 0 0
Законы Моргана позволяют реализовать функциональные полные системы на элементах только первого типа И-НЕ (ИЛИ-НЕ). Это означает, что абсолютно любую логическую задачу можно решить на первом типе логических элементов, реализуя в виде логических микросхем.