
- •Конспект лекций по имитационному моделированию
- •Тема 1. Вводная лекция
- •Применение имитационного моделирования
- •Место имитационного моделирования в математическом моделировании
- •Преимущества и недостатки имитационного моделирования
- •Основные принципы моделирования
- •Структура имитационных моделей
- •Тема 2. Технология имитационного моделирования
- •Алгоритм моделирования
- •Этапы имитационного моделирования
- •Тема 3. Метод Монте-Карло и имитационное моделирование
- •Тема 4. Планирование имитационных экспериментов
- •Тема 5. Обобщение и статистическая оценка результатов имитационного моделирования
- •Оценка качества имитационной модели
- •Методика применения планирования эксперимента
- •Определение необходимого количества параллельных опытов
- •Проверка однородности дисперсий
- •Проверка значимости коэффициентов регрессии
- •Проверка адекватности функции отклика
- •Тема 6. Имитационное моделирование и системы массового обслуживания
- •Информационно-вычислительного обслуживания
- •Тема 7. Прогнозирование экономических систем на основе марковских моделей
Тема 2. Технология имитационного моделирования
Алгоритм моделирования
Этапы имитационного моделирования
Алгоритм моделирования
Имитационное моделирование позволяет исследовать процессы во времени. Естественно, что действительная скорость протекания большинства исследуемых процессов значительно отличается от скорости моделирования на ЭВМ. Поэтому при использовании имитационного моделирования необходимо соотносить между собой три представления времени: реальное, модельное (системное) и машинное.
Под реальным подразумевают время, в котором исследуемая система работает в действительности. Здесь могут быть миллисекунды, минуты, часы, смены, месяцы, годы и т.д.
В масштабе модельного времени организуется работа самой имитационной модели. Это условные единицы времени, выраженные как целыми, так и действительными числами.
Машинное время отражает реальные затраты времени ЭВМ на проведение моделирования. В связи с ростом вычислительной мощности ЭВМ, значимо только при использовании достаточно сложных моделей.
Понятие модельного времени служит для решения следующих задач:
отображения перехода моделируемой системы из одного состояния в другое;
синхронизации работы компонент модели;
изменения масштаба времени функционирования исследуемой системы;
управления ходом модельного времени;
моделирования квазипараллельной обработки событий в модели.
Под квазипараллельной понимают последовательную обработку событий, которые в исследуемой системе происходят одновременно.
Модельное время может быть реализовано двумя методами – с постоянным шагом и по особым состояниям.
Если используется принцип постоянного шага, отсчет модельного времени ведется через фиксированные интервалы t, на которые разбит весь моделируемый период времени. События в модели считаются наступившими в момент окончания такого интервала. Состояние системы определяется для момента времени t, затем t+t , t+2t и т.д. Погрешности временных характеристик исследуемой системы зависят от величины t.
Метод постоянного шага целесообразно применять, если:
события появляются регулярно, их распределение во времени достаточно равномерно;
число событий велико и моменты появления их близки;
невозможно заранее определить моменты появления событий.
Этот метод достаточно легко реализовать даже с использованием универсальных языков программирования. Но нужно учесть, что придется определять состояние системы в каждый из моментов времени, даже если в нем не происходит никаких событий. А такие «пустые» отрезки времени могут быть весьма большими. В случае сложных моделей даже современная ЭВМ может «завязнуть» надолго.
Алгоритм моделирования по принципу постоянного шага приведен на рисунке 1.1. Здесь tМ – текущее значение модельного времени, z(tМ) – состояние системы в этот момент времени, TМ – интервал моделирования.
При моделировании по особым состояниям модельное время изменяется от события к событию. События обрабатываются в порядке их наступления, а одновременно наступившими считаются только те, которые являются одновременными в действительности. Алгоритм метода приведен на рисунке 1.2.
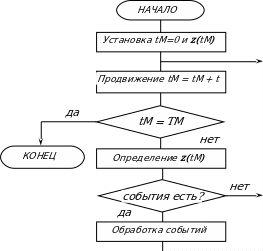
Рисунок 1.1 – Алгоритм моделирования с постоянным шагом
Моделирование по особым состояниям целесообразно, если:
события появляются нерегулярно либо интервалы между ними велики;
предъявляются повышенные требования к точности взаимного положения событий во времени;
необходимо реализовать квазипараллельную обработку одновременных событий.
Недостатком метода можно считать относительную сложность в реализации, т.к. для него требуется разработка специальной процедуры планирования событий (календаря событий). Главное достоинство ― «пропуск» участков на временной оси, где не происходит никаких событий.

Рисунок 1.2 – Алгоритм моделирования по особым состояниям
В отличие от других видов и способов математического моделирования с применением ЭВМ имитационное моделирование имеет свою специфику: запуск в компьютере взаимодействующих вычислительных процессов, которые являются по своим временным параметрам ― с точностью до масштабов времени и пространства ― аналогами исследуемых процессов.
