4.1 Класична теорія електропровідності. Рухомість носіїв заряду, питомий опір та провідність

Скорость дрейфа – скорость направленного движения

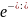
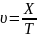где Х- суммарное расстояние, пройденное :

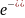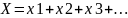Т суммарное время, кот. проходят

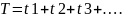Электрическое поле напряженности E сообщит электрону с мас­сой т ускорение, равное:

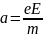
тогда приобретет скорость за время свобод. пробега :

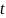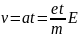
Пройденный путь составит:

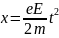
Чтобы найти общее расстояние, пройденное по полю, надо взять интеграл:

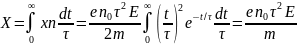
Отсюда скорость дрейфа равна:

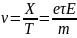
Скорость прямопропорциональна напряженности поля, времени свободного пробега и обратнопропорциональна массе . Величина, связывающая дрейфовую скорость с напряженностью, – подвижность носителей заряда .

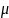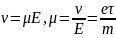
т. е. подвижность равна скорости дрейфа в электрическом поле единичной напряженности.

Плотность тока равна:

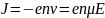
Используя З. Ома, получим удельную проводимость:

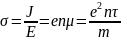
Удельное сопротивление – это обратная величина удельной проводимости.

Для МЕ удельное сопротивление растет с температурой:

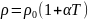
Для п/п характер температурной зависимости удельного сопротивления иной. Для некоторого интервала температур эта зависимость имеет вид:

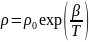
где β — некоторая постоянная для данного интервала тем­ператур, характеризующая тип п/п. Такие зависимости уд. сопротивления от температуры имеют невырожденные п/п.

4.5. Явление Холла.

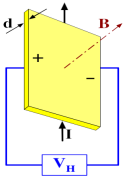
Эффект Холла— явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота. В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле В течет (текёт) электрический ток под действием напряженности Е. Магнитное поле будет отклонять носители заряда (для определенности электроны) от их движения вдоль или против электрического поля к одной из граней бруса. Таким образом, сила Лоренца приведет к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов Е1 не скомпенсирует магнитную составляющую силы Лоренца:

С корость электронов v можно выразить через плотность тока:

где n — концентрация носителей заряда. Тогда:

Коэффициент: 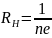пропорциональности между E₁ и jB называется коэффициентом (или констант-ой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как алюминий, цинк, железо, кобальт), в сильных полях наблюдается положительный знак R_H, что объясняется в полуклассической и квантовой теориях твёрдого тела.

4.2 Статистика электронов и дырок в полупроводниках. Плотность квантовых состояний. Функция распределения Ферми - Дирака для электронов и дырок.

Д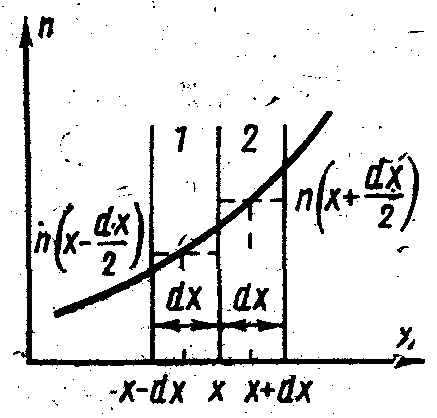 ля опреде­ления числа частиц, необходимо знать число квантовых со­стояний и вероятность нахождения частиц в этих состояниях. согласно определению: N(E)=dZ/dE (1). Если вероятность заполнения состояний с энергией Е равна f (Е, Т), то число электронов dn, находящихся в состояниях dZ, составит величину dn= f(E,T)dZ= f(E, T)N(E)dE (2) Найдем выражение для плотности квантовых состояний в слу­чае, когда поверхности равной энергии З.П. и В.З. являются сферами. (3) где Е_с = Е (р₀) - энергия электрона у дна З.П; m_n*- эффективная масса электрона.

Рис.1. Объем слоя в зоне Бриллюэна.

В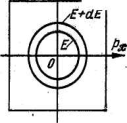 ыделим шаровой слой, заключенный между двумя изоэнергетическими поверх­ностями, соответствующими энергии Е(р) = const и Е(р) + dE = const (рис. 1). Объем этого слоя составляет величину: dVp=4πp²dp (4)

В каждой ячейке могут находиться два електрона с противоположно направленными спинами. С учетом этого число состояний в объеме dVp равно: (5) Исходя из равенства (3) (6) Откуда (7) Подставив (5), (6), (7) в соотнош. (1): (8) Определим плотность состояний вблизи верхнего края В. З. Для энергии дырок: (9) Здесь Еv = Е(р₀)-энергия дырки у потолка В.З.; mp*- эффективная масса дырки. Из расчетов, аналогичных про­деланным выше, будем иметь:

( 10) Т.е., если энергия носителей заряда является квадратичной функцией квазиимпульса, то плотность состояний N(Е) имеет зависимость от энергии вида (Е— Ес)^1/2 или (Еv — Е) ^1/2.. Поскольку pox=poy=poz=0,a E(po)=Ec, то

(11) где- 1/m1,1/m2,1/m3 –диагональные компоненты тензора обратной эффективной массы. Изоэнергетические поверхности в этом случае представляют собой эллипсоиды, уравнение кот. в канонической форме имеет вид:

( 12) Объем эллипсоида с полуосями a, b, c равен:

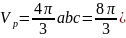
Объем слоя заключенного между двумя эллипсоидами равной энергии Е=const и E+dE=const, будет:

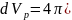
(14)В объеме dVp с учетом спина заключено следующее кол-во квантовых состояний:

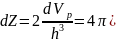
(15) Поэтому выраж. для плотности состояний у дна сложной З.П. примет вид:

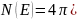
Если положить m1m2m3=mdn*³ , где mdn* - эф. масса плотности состояний для электронов. При этом, как и для простой зоны получим:

(17) Плотность состояний для кремния и германия. Для кремния m1=m2 (18)Изоэнергетические поверхности обеих зон можно заменить одной приведенной сферой с плотностью состояний: Для Ge выраж. (17).

Ф-ція розподілу Фермі-Дірака для електор. та дірок.,подчиняющихся принципу Паули, справедливо распределение Ферми-Дирака:

где k — постоянная Больцмана; Т — абсолютная тем-ра; F — энергия Ферми или химич. потенциал, т. е. работа, ко­т. необходимо затратить для изменения числа частиц в системе на единицу. Рассмотрим вид ф-ции распред. Ферми-Дирака при различных тем-рах. Из соотнош. (1) видно, что в случае Т=0 в интервале энергии 0≤Е<F имеем fo=1 и fo=0 для Е>F. Это означает, что все квантовые состояния с энергией, меньшей энергии Ферми, заняты электронами, а уровни, лежащие выше уровня. Ферми, полностью свободны, не заняты электро­нами. Следоват., энергия Ферми есть максимально возможная энергия электронов в металле при т-ре абсол. нуля. Рассмотрим случай, когда Т>0. Из выраж (1) для знач. энергии, равной знач. энергии Ферми (Е=F), имеем fo =1/2.Т.о., ур. Ферми есть энергетический уровень, вероятность заполнения кот. при т-ре, отличной от абсол. нуля, равна 0,5. Вероятность заполнения состояний за­метно отличается от единицы или нуля лишь в пределах (2÷3) kT вблизи значения Е = F .

. Вид ф-ции распределения

Ф-Д.