Прямоугольник и его свойства

Прямоугольник — это параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны.

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

В прямоугольном треугольнике центром описанной окружности является середина гипотенузы.

Ромб и его свойства

По определению, ромб — это параллелограмм, все стороны которого равны.

Свойства ромба:

1. Диагонали ромба перпендикулярны.

2. Диагонали ромба делят его углы пополам.

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны. 

Можно дать и другое определение квадрата: 

квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Перечислим свойства квадрата:

1. Все углы квадрата — прямые, все стороны квадрата — равны.

2. Диагонали квадрата равны и пересекаются под прямым углом.

3. Диагонали квадрата делят его углы пополам.

Площадь квадрата, очевидно, равна квадрату его стороны: S = a². 

Диагональ квадрата равна произведению его стороны на  , то есть  ,

Трапеция и ее свойства

Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — нет.

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны. 

Если боковые стороны равны, трапеция называется равнобедренной.

Площадь трапеции равна произведению полусуммы оснований на высоту: 

Отрезок, соединяющий середины оснований трапеции, называется средней линией трапеции.

Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме оснований: 

Окружность. Центральный и вписанный угол

Центральный угол — это угол, вершина которого находится в центре окружности. 

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.

На рисунке — центральные и вписанные углы, а также их важнейшие свойства.

Итак, величина центрального угла равна угловой величине дуги, на которую он опирается.

Значит, центральный угол величиной в 90 градусов будет опираться на дугу, равную 90°, то есть   круга. Центральный угол, равный 60°, опирается на дугу в 60 градусов, то есть на шестую часть круга.

Величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.

Также для решения задач нам понадобится понятие «хорда».

Равные центральные углы опираются на равные хорды.

Касательная к окружности

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности.

Тогда окружность называется описанной вокруг треугольника. 

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности. 

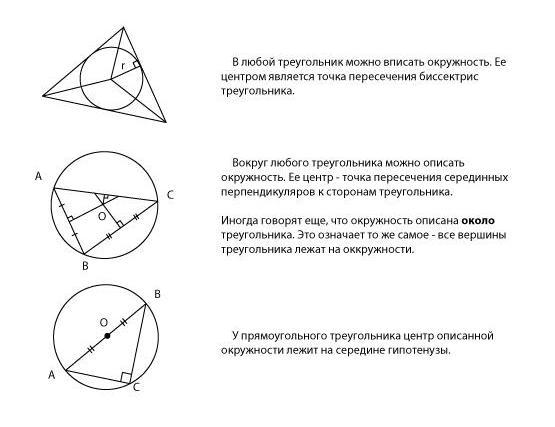
Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон.

Тогда сам треугольник будет описанным вокруг окружности.

Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности. 

В любой треугольник можно вписать окружность, причем только одну.

Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

S = p r

где p =   (a+b+c) — полупериметр, 

r — радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части С:

где a, b, c — стороны треугольника, R — радиус описанной окружности.

Для любого треугольника верна теорема синусов: