Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90º. Другими словами, половина развернутого угла.

Острый угол — меньший 90º.

Тупой угол — больший 90º. Применительно к такому углу «тупой» — не оскорбление, а математический термин :-)

Нарисуем прямоугольный треугольник.

Прямой угол обычно обозначается С. 

Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой.

Так, сторона, лежащая напротив угла А, обозначается а.

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет а, лежащий напротив угла А, называется противолежащим(по отношению к углу А).

Другой катет b, который лежит на одной из сторон угла А — прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе: 

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе: 

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: 

Другое определение: тангенсом острого угла называется отношение синуса угла к его косинусу: 

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или отношение косинуса к синусу): 

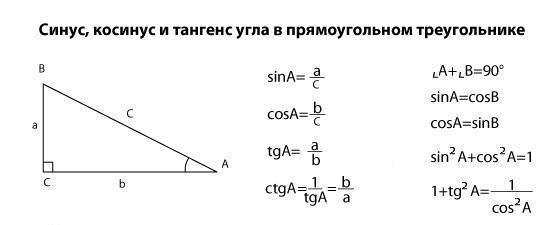
Это теорема Пифагора: a² + b² = с².

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для углов от 0 до 90°.

φ	0º	30º	45º	60º	90º
sin φ
cosφ
tg φ					не существует
ctg φ	не существует

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

Давайте вспомним сначала, что такое смежные углы.

Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна 180 градусов.

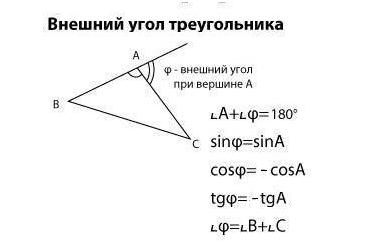
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине А — это угол, смежный с углом А.

 Если угол А острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что 

sin (180°-α) = sin α cos (180°-α) = - cos α tg (180°-α) = - tg α

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Высота в прямоугольном треугольнике

Вспомним, что высота в треугольнике — это перпендикуляр, опущенный из его вершины на противоположную сторону.

Высота проведена к гипотенузе АВ.

Она делит треугольник АВС на два прямоугольных треугольника — АСН и СНВ. Смотрим внимательно на рисунок и находим на нем равные углы.

Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна 90º. Значит, ∠ АСН = 90º - ∠ САН, то есть угол АСН равен углу АВС. Аналогично, угол САВ равен углу НСВ.

Иными словами, каждый из трех углов треугольника АВС равен одному из углов треугольника АСН (и треугольникаВСН). Треугольники АВС, АСН и ВСН называются подобными. Давайте нарисуем их рядом друг с другом.

Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники АСН и АВС. Стороны треугольника АВС длиннее, чем стороны треугольника АСН в k раз, причем  .

При решении задач нам пригодится равенство углов треугольников АВС, АСН и ВСН, а также пропорциональность их сторон.

Обратите также внимание, что площадь треугольника АВС можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.

 

Сумма углов треугольника

Сумма треугольника равна 180 градусов.

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые а и b. При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть  ∠1 = ∠3, ∠2 = ∠4.

Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна 180º.

1 и 7, 4 и 6 — накрест лежащие. Накрест лежащие углы равны.  ∠1 = ∠7,  ∠4 = ∠6.

Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние.Сумма односторонних углов равна 180°, то есть  ∠1 + ∠6 = 180°,  ∠4 + ∠7 = 180°.

Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и 8) называются соответственными.

Соответственные углы равны, то есть  ∠2 = ∠6,  ∠3 = ∠7.

Элементы треугольника. Высоты, медианы, биссектрисы

Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии.

Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают.

Затем — подробные объяснения и решение задач.

Напомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.

Попробуйте провести три высоты в тупоугольном треугольнике.

Получилось? Да, редкий выпускник справляется с этим заданием.

Действительно, мы не можем опустить перпендикуляр из точки А на отрезок ВС, зато можем опустить его на прямую ВС — то есть на продолжение стороны ВС.

В этом случае в одной точке пересекаются не сами высоты, а их продолжения.

А как выглядят три высоты в прямоугольном треугольнике? В какой точке они пересекаются?

Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.

Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

У биссектрисы угла есть замечательное свойство — точки, принадлежащие ей, равноудалены от сторон угла.

Поэтому три биссектрисы треугольника пересекаются в одной точке, равноудаленной от всех сторон треугольника.

Эта точка является центром окружности, вписанной в треугольник.

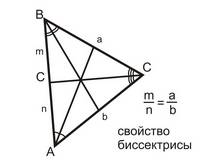
Еще одно свойство биссектрисы пригодится тем, кто собирается решать задачу С4. Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.

Четырехугольники. Сумма углов четырехугольника. Параллелограмм. Виды параллелограммов и их свойства. Ромб, прямоугольник, квадрат. Трапеция и ее свойства

В школьных задачах по геометрии мы обычно рассматриваем выпуклые четырехугольники.

В чем разница между ними?

Если любые две точки выпуклого многоугольника соединить отрезком — весь отрезок будет лежать внутри многоугольника.

Для невыпуклых фигур это не выполняется.

Сумма углов выпуклого четырехугольника равна 360 градусов.

Произвольные четырехугольники в задачах по геометрии встречаются редко.

Намного чаще — такие, у которых есть параллельные стороны.

Это параллелограмм, ромб, квадрат, прямоугольник и трапеция.  Здесь в таблице собраны их определения и свойства.

Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма

Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон. 

Свойства параллелограмма:

1. Противоположные стороны параллелограмма равны.

2. Противоположные углы параллелограмма равны.

3. Диагонали параллелограмма в точке пересечения делятся пополам.

Биссектрисы углов параллелограмма, прилежащих к одной стороне, — перпендикулярны.

Легко доказывается и другое свойство биссектрис параллелограмма:

Биссектрисы противоположных углов параллелограмма — параллельны.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Запишем формулы площади параллелограмма:

S = ah, где а — основание параллелограмма, h — его высота. 

S = ab sin φ, где а и b — стороны параллелограмма, φ — угол между ними.

S =   d1 d2 sin α, где d1 и d2 — диагонали параллелограмма, α — угол между ними.