Проверка выдвинутой гипотезы с помощью критерия Пирсона

Критерий c²:

Предварительно вариационный ряд достаточно произвольно делится на k субинтервалов величиной 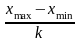. Основное требование: в каждый граничный субинтервал должно попасть не менее одного наблюдения ( ), а в остальные – не менее 5 наблюдений (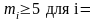 2, 3, …, k–1), в противном случае число субинтервалов уменьшают. На основе такого деления строится гистограмма результатов наблюдения и рассчитывается p_i – теоретическая вероятность гипотетического (выдвинутого в гипотезе) закона распределения. При этом, как показано Пирсоном, величина

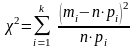, где m_i – число наблюдений в субинтервале i

в предположении, что гипотеза верна, имеет асимптотическое c² распределение с m=k–1 степенями свободы. Так как значение c² есть мера отклонения реального отклонения от гипотетического, то гипотеза отвергается, если вычисленное значение c² превысит определенное критическое значение 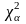( 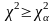), зависящее от m и заданного уровня значимости a (обычно от 0.1 до 0.01), приведенное в таблице 6.

таблица 6

m	a			m		a
	0.1	0.05	0.01			0.1		0.05	0.01
1	2.7	3.8	6.6	6	10.6		12.6	16.8
2	4.6	5.9	9.2	7	12.0		14.1	18.5
3	6.3	7.8	11.3	8	13.4		15.5	20.1
4	7.8	9.5	13.3	9	14.7		16.9	21.7
5	9.5	11.1	15.1	10	16.0		18.3	23.2

Обнаружение ухода систематической погрешности

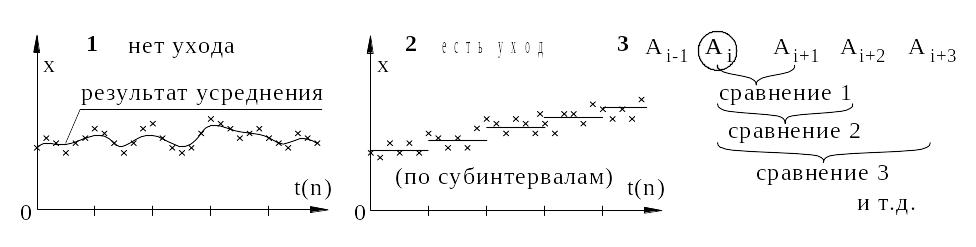
Рис. 1 Примеры изменения x при наличии (2) и отсутствии (1) ухода

систематической погрешности. Пример процедуры подсчета числа инверсий

A_i на основе сравнения 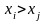(h_i,j=1)

Уход систематической погрешности при неизменной измеряемой величине x_меры можно примерно оценить графически, см. рис. 1, разбивая интервал наблюдения (ряд значений 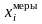) на несколько субинтервалов или интегрируя полученное значение с постоянной времени, намного меньшей, чем весь интервал наблюдения. Другим способом обнаружения ухода систематической погрешности является применение специальных методик обработки ряда значений , таких как метод наименьших квадратов (позволяет определить вид зависимости систематической погрешности от времени) или критерий тренда (позволяет определить только сам факт монотонного ухода систематической погрешности).

Критерий тренда:

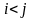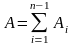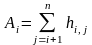Для ряда значений объемом n рассматриваются все неравенства вида , где . Каждое такое неравенство называют инверсией. В итоге подсчитывается общее число таких инверсий , где , а 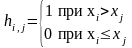, см. рис. 1. Если анализируемая последовательность не содержит медленных изменений 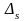, то число инверсий – дискретная случайная величина с плотностью вероятности p(A), зависящей только от n и математическим ожиданием 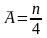. 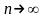При закон распределения р(А) нормализуется. Гипотеза о существовании ухода систематической погрешности оценивается по таблице 7, задающей нижнюю A_н и верхнюю А_в границы числа инверсий с заданным уровнем значимости a.

таблица 7

n	a = 0.1		a = 0.05
	Aн	Ав	Ан	Ав
10	13	31	11	33
14	30	60	27	63
20	69	120	64	125
30	171	263	162	272
50	756	1013	731	1038

Если анализируемая последовательность не содержит медленных изменений , то общее число инверсий должно находиться в интервале от A_н до А_в , в противном случае принимается гипотеза об уходе систематической погрешности.