
- •Содержание
- •1 Моделирование
- •1.1 Место моделирования в научном познании
- •1.2 Виды моделирования
- •1.3 Математическое моделирование
- •1.4 Системный подход к моделированию
- •1.5 Параметры математических моделей
- •Внешняя среда анализируемая система .
- •1.6 Методы реализации математических моделей
- •1.7 Этапы построения математических моделей
- •1.8 Требования к математическим моделям
- •2 Типы математических моделей
- •2.1 Структурные модели
- •2.2 Теоретико-множественные модели
- •2.3 Модели формальных систем
- •2.4 Геометрическое моделирование
- •2.5 Функциональное моделирование
- •2.6 Обработка экспериментальных данных
- •2.7 Математические модели объектов на микроуровне
- •2.8 Математические модели на основе фундаментальных законов сохранения
- •2.9 Метод конечных элементов
- •2.10 Математические модели объектов на макроуровне
- •2.11 Моделирование нелинейных систем
- •2.12 Оптимизационные модели
- •2.13 Решение задачи линейного программирования
- •2.14 Моделирование в условиях неопределенности
- •2.15 Имитационное моделирование
- •2.16 Системы массового обслуживания
- •2.17 Клеточные автоматы
- •2.18 Модели теории игр
- •4 Вопросы для контроля
- •Литература
2.13 Решение задачи линейного программирования
Основным инструментом решения задач линейного программирования является симплекс-метод. Он хорошо разработан и реализован в профессиональном программном обеспечении. В этом разделе рассматривается графический метод, который более прост, но вместе с тем придает наглядность процессу поиска оптимального решения.
Ниже рассматривается задача на ограниченные ресурсы.
Пусть для производства двух видов деталей Д1 и Д2 требуются задействовать токарные, фрезерные и шлифовальные станки. Наличие станков каждого вида и их количество, необходимое для выпуска одной партии продукции, приведены в таблице 6. Там же указана ожидаемая прибыль, которую принесет выпуск соответствующей партии деталей. Необходимо найти план выпуска продукции, позволяющий получить максимальную прибыль.
Таблица 6 – Исходные данные
Характеристика |
Продукция |
Наличие станков в цехе |
||
Д1 |
Д2 |
|||
Станки |
Токарные |
1 |
3 |
21 |
Фрезерные |
3 |
2 |
21 |
|
Шлифовальные |
3 |
1 |
18 |
|
|
Прибыль |
30 |
60 |
|
|
Количество партий деталей |
|
|
|
Сформируем математические соотношения, необходимые для решения задачи.
Обозначим
![]() критерий оптимальности задачи –
максимальную прибыль, тогда целевая
функция максимизации прибыли будет
иметь вид:
критерий оптимальности задачи –
максимальную прибыль, тогда целевая
функция максимизации прибыли будет
иметь вид:
![]() . (28)
. (28)
Ограничения, входящие в математическую модель этой задачи, можно записать в виде системы линейных неравенств:
 . (29)
. (29)
Первые два неравенства задают лимиты на количество использованных станков, соответственно токарных, фрезерных и шлифовальных. Последние два неравенства показывают, что выпуск продукции не может быть отрицательным.
Построим графическое изображение системы неравенств (29), для удобства представив ее в форме, аналогичной уравнениям прямой в отрезках:
 . (30)
. (30)
Система (30) построена на рисунке 25. Решением этой системы неравенств являются координаты всех точек, принадлежащих области, называемой областью допустимых решений задачи линейного программирования, т.е. закрашенному многоугольнику.
Решением исходной задачи будет одна (в частном случае несколько штук) из бесчисленного множества точек, входящих в область допустимых решений.
Представим целевую функцию (1) в форме уравнения прямой с угловым коэффициентом:
![]() .
.
Обозначим
![]() ,
где
- произвольное числовое значение.
,
где
- произвольное числовое значение.

Рисунок 25 – Область допустимых решений
Меняя значение , в выражении
![]()
можно получить семейство параллельных прямых, называемых линиями уровня. Проведем одну из таких прямых через начало координат (рисунок 26).
Определим вектор градиент линейной функции :
![]() .
.
Чтобы
построить этот вектор, надо соединить
начало координат с точкой
![]() .
Но для удобства можно строить вектор
пропорциональный вектору
.
Но для удобства можно строить вектор
пропорциональный вектору
![]() .
При максимизации целевой функции прямая
.
При максимизации целевой функции прямая
![]() передвигается параллельно самой себе
в направлении вектора градиента, а при
минимизации – в противоположном
направлении.
передвигается параллельно самой себе
в направлении вектора градиента, а при
минимизации – в противоположном
направлении.
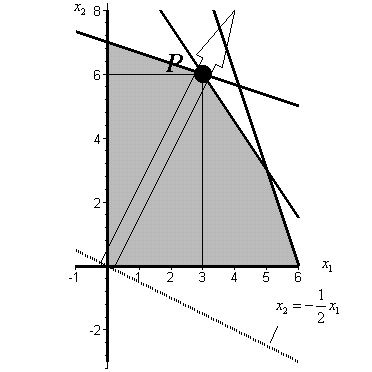
Рисунок 26 – Нахождение оптимума
В
нашем случае движение построенной линии
уровня будем осуществлять до ее
пересечения с точкой
;
далее прямая выходит из области допустимых
решений. Именно в точке
,
при
![]() и
и
![]() ,
достигается максимум прибыли (рисунок
2):
,
достигается максимум прибыли (рисунок
2):
![]() .
.
В частном случае, когда одна из сторон области допустимых решений параллельна линии уровня, задача может иметь несколько оптимальных решений, т.е. различный набор значений искомых переменных будет придавать одно и то же значение целевой функции.
