(8)Классификация разрывов функции
1) Функция
разрывна в
,
когда
либо не существует, либо существует но
не равен
Пусть
существует. В этом случае разрыв называют
устранимым (назначают в
значение р)
Пример:
2) Пусть не существует - внутренняя точка , тогда непрерывность в означает непрерывность как слева так и справа разрывность в означает наличие разрыва хотя бы с одной стороны.
Определение:
Функция
имеет в точке
справа (слева) разрыв первого рода, если
и разрыв второго рода, если этот
односторонний предел не существует или
бесконечен.
Пример:
Определение:
Двусторонний разрыв называется разрывом первого рода, если односторонние разрывы только первого рода и второго рода в противном случае.
(9)Задачи, приводящие к понятию производной. Производная функции.
1) Задачи, приводящие к понятию производной.
1. Пусть материальная
точка m
движется вдоль направления прямой S,
по закону S(t),
в момент
времени
точка находилась в
,
через время
(т.е.
в момент времени
)
точка переместилась
,
мгновенной скоростью движения в момент
равный
,
назовём
.
2. Пусть имеется плоская кривая l,
Определение:
предельное положение секущей при
,
называется касательной к l
в точке
,
т.е. если
между секущей и некоторой кривой
стремится к определённому пределу
,
при расстоянии между
,
то прямую проходящую через
называют касательной.
Задача:
Пусть кривая
l
задаётся
функцией y=f(x),
допустим,
сто в точке
к
ней существует касательная, причем
наклонная(т.е. составляет с положительным
направлением оси угол
)
;
,
-угол
наклона касательной, значит
Итак, в разных задачах пришли к решению однотипных задач.
2) Понятия.
Пусть y=f(x),
Определение:
производной функции f(x)
в точке
наз.
(вводя
)
.
формула(1)- физический смысл производной,
формула (2)- геометрический.
Производные:
1)
2)
Функция имеет смысл. Берём
фиксируем
,
;
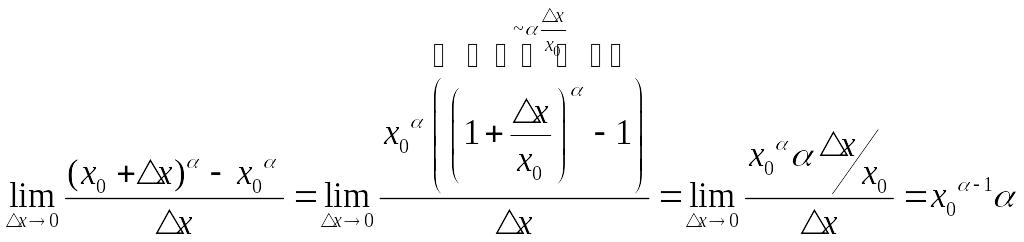3)
;
;
4)
,
,
;
5)
;
;
;
(10)Основные правила вычисления производных:формула для приращения функции, производная результатов арифметических действий.
1) Формула для приращения функции
Пусть f(x)
имеет конечную производную в точке
,
,
-
б.м.ф. по сравнению с
.
Формула
для приращения функции, для любого
.
Следствие из
(1): Если f(x)
имеет конечную
производную в точке
то
она непрерывна в
.
Док-во:
Непрерывность на языке приращения
означает, что
т.е. приращение при
Теорема: (о производной результатов арифметических действий) Если f(x),g(x): Е →R и в точке имеют конечные производные, то:
1)
2)
3)
,
Док-во:
обозначим через
,
зададим
приращ.
,
при этом f(x),g(x)
получат
тогда:
;
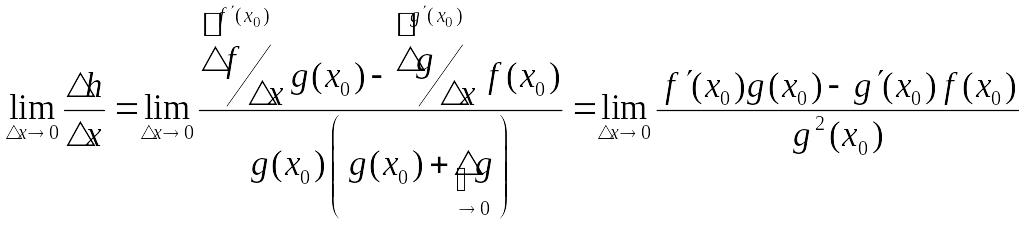
Следствие1:
(из теоремы 1 пункт)
Следствие2:
Следствие3:
константу модно выносить за знак
производной:
,
(11)Основные правила вычисления производной: производная обратной функции, производная сложной функции.
Производная обратной функции
Теорема: Пусть f(x): Е →R, если
1) существует однозначная, обратная и f(x) функции,
2) существует
конечная производная
и
непрерывна,
,
то существует
Док-во:
фиксируем точку
,
дадим ей приращение
,
и рассмотрим
Геометрический
смысл теоремы:
Рассмотрим функцию
в отрезке
.
Обратная функция
,
,
;
;
;