Литература
1. Бессонов Л. А. Теоретические основы электротехники. Электромагнитное поле. М.: Высшая школа, 1978.
2. Даревский А. И., Кухаркин Е. С. Теоретические основы электротехники. Ч.2. - М.: Высшая школа, 1965.
3. Татур Т. А. Основы теории электромагнитного поля. Справочное пособие. М.: Высшая школа, 1989.
4. Методические указания к выполнению курсовой работы. Сумы: Ризоцентр СумГУ, 1998.
5.Бронштейн И. Н., Семедяев К. К. Справочник по математике.-М.: Наука, 1964 г.
Приложение а
#include<conio.h>
#include<iostream.h>
#Include<graphics,h>
#include<stdlib.h>
#include<math.h>
#define ЕЕ sqrt((E0*R^2-1)sin(a))^2+(E0(R^2/r^2+1)cos(a))^2)
#define EI 0
#define R 0.08
#define EO 50*10^3
double E0,R,r,a,EE,EI,step,max;
char c,num;
int i,j,dr^DETECT,mod,m,n;
double cos_sin(double aa, int q)
void main()
R=0;
step=R-1;
a=0;
step=a+1;
i=0
i<12
step=1+i
{if(a>360)
a=0;
return (sqrt((E0*R^2-1)sin(a))^2+(E0(R^2/r^2+1)cos(a))^2));
else
return (sqrt((E0*R^2-1)sin(a))^2+(E0(R^2/r^2+1)cos(a))^2));}
initgraph(&dr,&mod,"D:\\Tp\\cppbb50\\grafbb5\\gfi");
setcolor(1);
circle(0,0,r)
line(5,5,5,10,1,3);
line(0,10,0,10,1,3);
setlinestyle(0,0,3);
settextstyle(1,0,2);
setbkcolor(WHITE);
line(0,10,i,R,a,2);
outtextxy(a,R,2);
a=0;
for(a-0;a<i-l;a++){
line(floor(sqrt((E0*R^2-1)sin(a))^2+(E0(R^2/r^2+1)cos(a))^2))),
floor(EE*(a+step)),EE-floor(EE*[a+l]));
a+=step;}
R=0;
for(R-0;R<i-l;R++)
{line(floor(sqrt((E0*R^2-1)sin(a))^2+(E0(R^2/r^2+1)cos(a))^2))),
floor(EE*(R+step)),EE-floor(EE*[R+l]));
R+step;
if(R>15)
R=0;
return (sqrt((E0*R^2-1)sin(a))^2+(E0(R^2/r^2+1)cos(a))^2));
else
return (sqrt((E0*R^2-1)sin(a))^2+(E0(R^2/r^2+1)cos(a))^2));}}
Приложение б
#include<conio.h>
#include<iostream.h>
#Include<graphics,h>
#include<stdlib.h>
#include<math.h>
#define HH H0/Ze*2*pi*a*b/{LamMa*a*n*n+b*b*m*m) )
#define pi 3.14159265358979
#define mx 639
#define my 479
#define vv Зе+8/sqrt(e)
double E0,Lam, Z,xry,z,lkr,l,e,a,b,kx,ky, step,max;
char c,num;
int i,j,dr^DETECT,mod,m,n;
double cos_sin(double xx,double yy,int q)
{
if(!q)
return (EE*sin(m*pi/a*xx)*cos(n*pi/b*yy));
else
return (EE*cos(m*pi/a*xx)*sin(n*pi/b*yy));
}
void main()
{ double
Ex[200],Ey[200] , Hx[200],Hy[200];
EO-50;
a=0.135;
b=0.065;
rn=1;
n=5;
e о г
lkr=2/sqrt(pow((m/a)r2)+pow((n/b),2)); 1=0.006;
Lam^l/sqrt(e-pow(1/lkr,2)); Z=sqrt(4e-7^pi/(e*8.85e-12)); num-1; for(;;)
cout«"\b \b";
gotoxy(1,1);
cout«"D";
num~l ;
}
}
else if(c=-'\x48')
{
if(num>l)
{
cout«"\b \b";
i=wherex();
j-wherey()-1;
gotoxy(i,j);
cout«"D";
nura;
}
else
{
cout«"\b \b";
gotoxy(1,7);
cout«"D";
num=7;
}
}
}
switch (num)
{
case 1:
{
x=0;
step=a/200;
max^O;
for(i=0;x<a;i++)
{
Ex[i]=m*b*cos_sin{b/4,x,1); if(max<fabs(Ex[i])) max=fabs(Ex[i]); Ey[i]=a*n*cos_sin(b/4,x,Q); if(max<fabs(Ey[i])) max=fabs(Ey[i]);
Hx[i]=-a*n*cos_sin(b/4,x,0); if(max<fabs(Hx[i])) max=fabs(Hx[i]); Ну[i]=b*m*cos_sin(b/4,x,1); if(max<fabs(Hy[i])) max^fabs(Ну[i]); x+=step;
}
initgraph(&dr,&mod,"C:\\bcpp3\\bgi");
setcolor(1);
setlinestyle(0,0,3);
settextstyle(1,0,2);
setbkcolor(WHITE);
line(0,my/2,mx,my/2);
line(0,0,0,my);
outtextxy(mx-30,my/2-30,"X");
outtextxy(30,70,"Ex(X)");
outtextxy(140,190,"Ey(Yj");
x=0;
kx=1500/a;
ky^!60/max;
for(j-0;j<i-l;j++){
line(floor(kx^x),my/2-floor(ky*Ex[j]) ,
floor(kx*(x+step)),my/2-floor(ky*Ex[j+l]));
x+=step;
}
x=0;
for(j-0;j<i-l;j++)
{
line(floor(kx*x),my/2-floor(ky*Ey[j]),
floor(kx*(x+step)),my/2-floor(ky*Ey[j+l]));
x+^step;
}
getch();
clearcievice () ;
line(0,my/2,rax,my/2);
line(0,0,0,my);
outtextxy(mx-30,my/2-30,"X");
outtextxy(140,50,"Hx(X}");
outtextxy(350,160,"Hy(X)");
x-0;
for(j=0;j<i-l;j++)
{
line(floor(kx*x),my/2-floor(ky*Hx[j]),
floor(kx*(x+step)),my/2-floor(ky*Hx[j+l]));
x+=step;
}
x=0;
for(j=0;j<i-l;j++){
line(floor(kx*x),my/2-floor(ky*Hy[j]),
floor(kx* (x+step) ) ,my/2-'floor(ky*Hy[j + l] ) ) ;
x+=step;
}
getch(); closegraph();
}
break;
case 2;
{
x=0;
step=b/2G0;
rnax=0;
for(i=0;x<b;i++)
{
Ex[i]=m*b*cos_sin(a/4,x,1}; if(max<fabs(Ex[i])) max^fabs(Ex[i]); Ey[i]=a*n*cos_sin(a/4,x,0); if(max<fabs(Ey[i])) max=fabs(Ey[i]); Hx[i]=-a*n*cos_sin(a/4,x,0); if(max<fabs(Hx[i])) max=fabs(Hx[i]); Ну[i]^b*m*cos_sin(a/4,x,1); if(max<fabs(Hy[i])) max=fabs(Ну[i]); x+^step;
}
initgraph(&dr,&mod,"C:\\bcpp3\\bgi");
setbkcolor(WHITE);
setcolor(1);
setlinestyle(0,0,3);
line(Q,my,mx,my);
line(mx/2,0,mx/2,my);
settextstyle(1,0,2);
outtextxy(mx/2+20/10,"Y") ;
outtextxy(340,80,"Ex(Y)");
outtextxy(60/100,"Ey(Y)") ;
x=0;
kx=20G/max;
ky=475/b;
for(j=0;j<i-l;j++){
line(mx/2+floGr(kx*Ex[j]),floor(ky*x),
mx/2+floor(kx*Ex[j+l]),floor(ky*(x+step)));
x+=step;
}
x=0;
for(j-0;j<i-l;j++)
{
line(mx/2+floor(kx*Ey[j]),floor(ky*x),
mx/2+floor(kx*Ey[j-M]),floor(ky*(x+step)));
x+=step;
}
getch (); cleardevice();
line (0,my,mx,my) ; line {mx/2, 0,mx/2,my) ; settextstyle(1,0,2); outtextxy(320-20,10,"Y"); outtextxy{60,220,"Hx(Y)"); outtextxy(350,30,"Ну(Y)"}; x^O; for(j=0;j<i-l;j++)
{
line(mx/2+floor(kx*Hx[j]),floor(ky*x),
mx/2+floor(kx*Hx[j+l]),floor(ky*(x+step)));
x+=step;
}
x^0;
for(j=0;j<i-l;j++)
{
line(mx/2+floor(kx*Hy[j]),floor(ky*x),
mx/2+floor (kx*Hy [ j + 1] ) , floor (ky* (x+step) ) ) ,-
x+=step;
}
getch();
closegraph();
} break;
case 3:
{
step=0.009;
max=0;
x-0;
for(i=0;x<l;i++)
{
Ex[i]=m*b*EE*cos(-x*2*pi/Lam); if(max<fabs(Ex[i])) max^fabs(Ex[i]) ;
Ey[i]=a*n*EE*cos(-l*x*2*pi/Lam); if(max<fabs(Ey[i])) max=fabs(Ey[i]) ;
Hx[i]=-a*n*EE*cos(-l*x*2*pi/Lam); if(max<fabs(Hx[i] )) max^fabs(Hx[i]) ;
Hy[i]=b*m*EE*cos(-l*x*2*pi/Lam); if(max<fabs(Hy[i])) max=fabs(Ну[i]); x+=step;
}
initgraph(&cir, &mod, "C: \\bcpp3\\bgi") ;
setcolor(DARKGRAY);
setbkcolor(WHITE) ;
setcolor(1);
setlinestyle(0, 0,3) ;
line{0,my/2,mx,my/2);
line(0r0,0,my);
settextstyle(1,0,2) ;
outtextxy(mx-30,my/2-10,"X");
outtextxy(130,260,"Ex(Z)");
outtextxy(30,8 0,"Ey(Z)");
x=0;
kx=3000;
ky=150/max;
for(j=0;j<i-l;j++)
{
line(floor(kx*x),my/2-floor(ky*Ex[j]),
floor(kx*(x+step)),my/2-floor(ky*Ex[j+l]));
x+=step;
}
x=0;
for(j=0;j<i-l;j++)
{
line(floor(kx*x) ,my/2- floor (ky*Ey[j] ) ,
floor(kx*(x+step)),my/2~floor(ky*Ey[j+l]));
x+=step;
}
getch();
cleardevice();
line (0,rny/2,mx,rny/2) ;
line(0,0,0,my) ;
outtextxy(mx-30,my/2-10/ "X");
outtextxy(130,65,"Hx(Z)");
outtextxy(130,260,"Hy(Z)");
x=0;
for(j=0;j<i-l;j++)
{
line(floor(kx*x),my/2~floor(ky^Hx[j]) , floor(kx*(x+step))rmy/2-floor(ky*Hx[j+l]));
Xt 5iGPf }
x=0;
for(j=0;j<i-l;j++)
{
line(floor(kx*x),my/2-floor(ky*Hy[j]), floor(kx*(x+step)),my/2-floor(ky*Hy[j+l])); x+=step;
}
getch(); closegraph(); } break; case 4:
{
x=0;
step=0.009;
max=0;
for(i=0;x<l;i++)
{ Ex[i]-E0*sin(-2*pi*x/Lam)' ;
if(max<fabs(Ex[i])) max=fabs(Ex[i]);
x+=step;
}
initgraph(&dr,&mod,"C:\\bcpp3\\bgi");
setbkcolorfWHITE);
setcolor(1) ;
setlinestyle(0,0,3);
line(10,10,10,479);
line{0,240,635,240);
setlinestyle(0,0,3);
settextstyle(1,0,2);
outtextxy(mx-50,my/2+8,"Z");
outtextxy(165,75,"Ez(Z)");
kx-3000;
ky=14 0/max;
x=0;
for(j=0;j<i-l;j++)
{
setcolor(1);
line(10+floor(kx*x),my/2-floor(ky*Ex[j]) ,
10+floor(kx*(x+step)),my/2-floor(ky*Ex[j+1]));
x+-step;
}
getch ();
closegraph();
}
break; case 5:
case 6:exit(0); default:break;
Приложение В
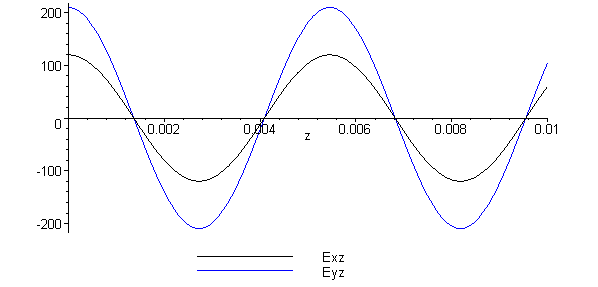
Результат построения
Епюра 1

Епюра 2 Епюра 3


Епюра 4 Епюра 5


Епюра 6 Епюра 7


Епюра 8 Епюра 9