
- •Оглавление
- •§1. Статистическое описание систем с большим числом степеней свободы
- •§2. Метод статистической физики(элементы теории вероятностей)
- •§3. Микро- и макро- параметры системы.
- •§4. Свойство эргодичности системы.
- •§5. Два способа усреднения в статистической физике
- •§6. Понятие ансамбля систем
- •§7. Эргодическая гипотеза
- •§8. Равновесное состояние системы
- •§9. Время релаксации
- •§10. Квазизамкнутость и статистическая независимость подсистем
- •§15. Микроканоническое распределение Гиббса
- •§16. Каноническое распределение Гиббса
- •§17. Принцип возрастания энтропии
- •§18*. Статистическая сумма и её свойства
- •§19*. Функция распределения вероятностей по энергии и распределение Гаусса
- •§20. Квазиклассическое приближение в статистической физике
- •§21*. Распределение Максвелла как следствие канонического распределения Гиббса
- •§22. Использование распределения Максвелла для расчёта средних: , , ,
- •§23. Большое каноническое распределение
- •§24. Термодинамический потенциал Гиббса
- •§25. Распределение Ферми-Дирака
- •§26. Распределение Бозе-Эйнштейна
- •§27. Ферми и Бозе газы элементарных частиц
- •§28. Расчёт импульса Ферми для электронного газа при
- •§29. Расчёт энергии электронного газа при
- •§30*. Уравнение состояния идеального электронного газа при . Критерий идеальности электронного газа
- •§31*. Числовые оценки параметров , , , , и
- •Экзаменационные вопросы по курсу “Статистическая физика”
- •Экзаменационные задачи по курсу “Статистическая физика”
- •Экзаменационные вопросы и задачи по курсу “Статистическая физика” (минимум)
- •Решение задач по курсу “Статистическая физика”
- •Гамма-функция Эйлера
Экзаменационные вопросы и задачи по курсу “Статистическая физика” (минимум)
Статистическое описание систем с большим числом степеней свободы.
Два способа усреднения в статистической физике.
Эргодическая гипотеза.
Теорема Лиувилля
Микроканоническое распределение Гиббса.
Каноническое распределение Гиббса
Квазиклассическое приближение в статистической физике.
Использование распределение Максвелла для расчета средних:
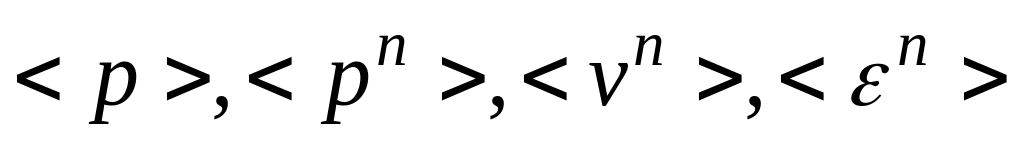
Распределение Ферми-Дирака.
Распределение Бозе-Эйнштейна.
Расчет импульса Ферми для электронного газа при Т=0.
Задачи:
Задача 1. Вероятность того, что и лежат в интервалах: и дается выражением:
Считая, что областями измерения переменных и является и , найти константу нормировки .
Задача 2. Используя распределение Максвелла, найти:
а) ;
б) ;
в) (наиболее вероятное значение величины скорости);
Задача 3: Используя распределение Максвелла, найти дисперсию кинетической энергии , где .
Задача 4. Найти центр тяжести столба идеального газа в однородном поле тяжести, если ускорение поля тяжести , масса молекулы , температура .
Решение задач по курсу “Статистическая физика”
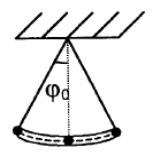
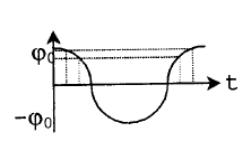
Задача 1. Математический маятник совершает гармонические колебания по закону
Найти вероятность того, что при случайном измерении отклонения маятника это значение будет лежать в интервале .
Решение. Запишем закон колебания в
виде:
![]() ,
где
,
где
![]() .
Тогда нам надо найти вероятность
.
Тогда нам надо найти вероятность
![]() .
.
Из рисунка видно, что
![]()
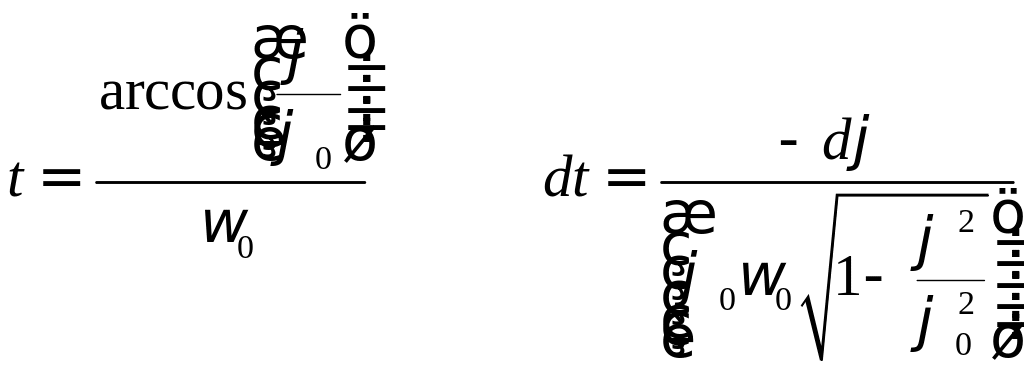
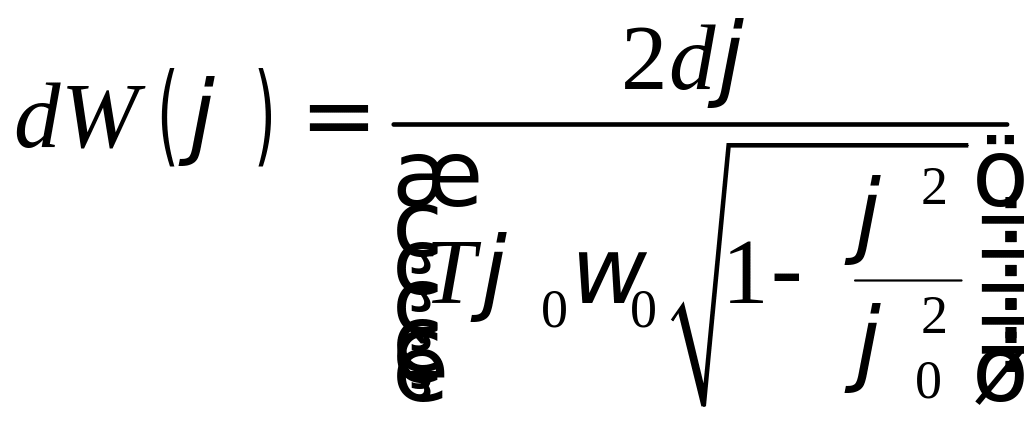
Обозначим
![]()

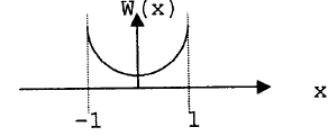
Как и ожидалось, площадь под кривой равна 1.
Ответ.
,
где
![]()
Дополнение. В общем случае график зависимости может не выражаться через линейные функции. Например:
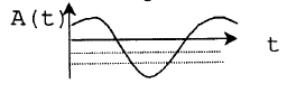
Тогда необходимо подсчитать время, в течении которого параметр начодится в заданном интервале значений:
![]()
Гамма-функция Эйлера
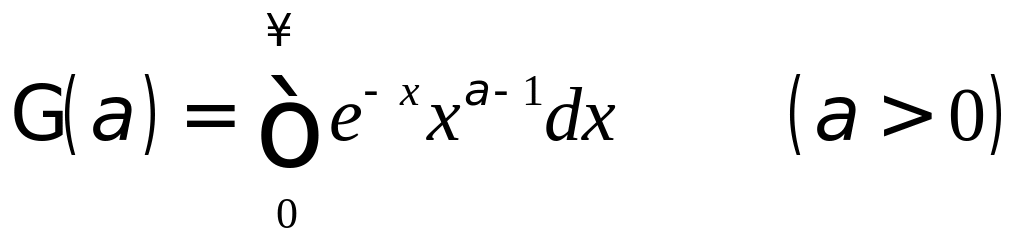
Свойства:
![]()
Задача 2. Вероятность того, что и лежат в интервалах: и дается выражением:
Считая, что областями измерения переменных и является и , найти константу нормировки .
Задача 3. Определить вероятность того, что значение величины будет лежать в интервале .
Решение. Условие нормировки:
![]()
![]() =1
=1
Переходим к полярным координатам:
![]() якобиан перехода:
якобиан перехода:
![]()
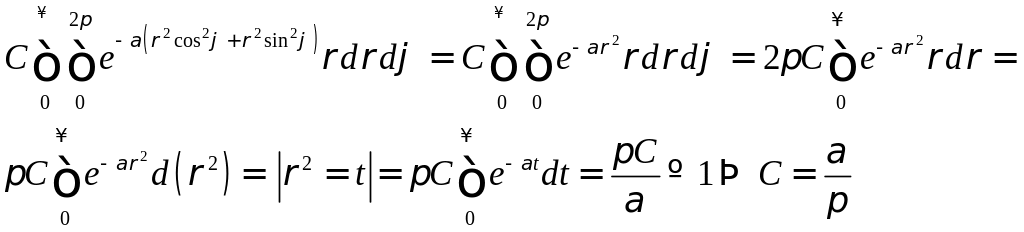
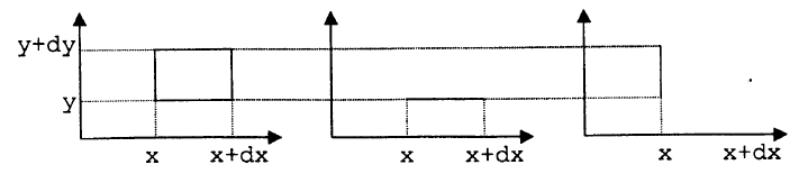
Первому рисунку отвечает функция
распределения
![]() ;
;
второму -
![]() ;
третьему -
;
третьему -
![]()
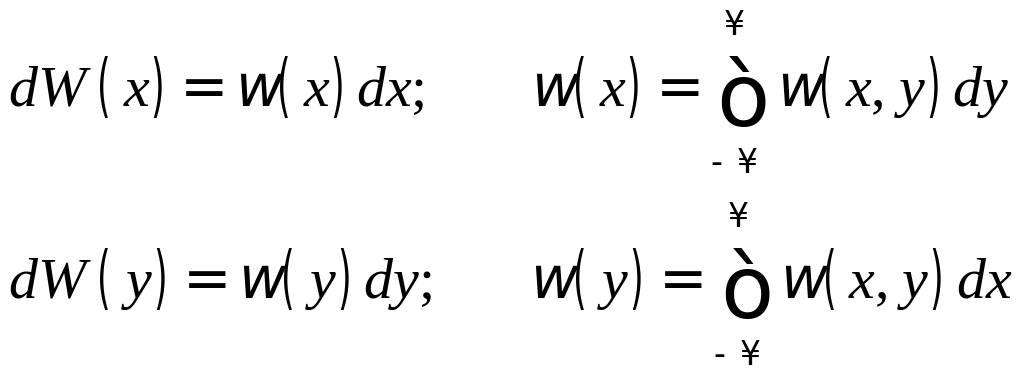
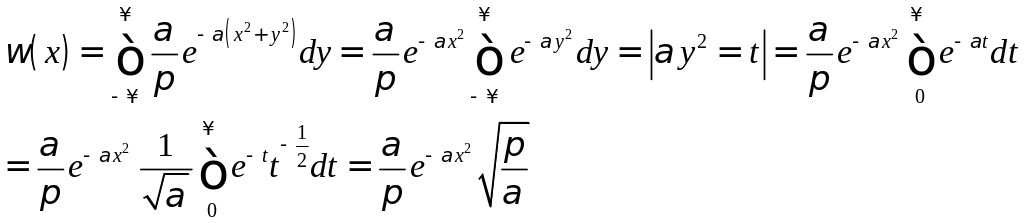
![]()
Аналогично:
![]()
Ответ:
![]()
Задача 4. Найти дисперсию энергии в случае канонического распределения Гиббса.
Решение.
![]()
![]()
![]()
Аналогично:
![]()
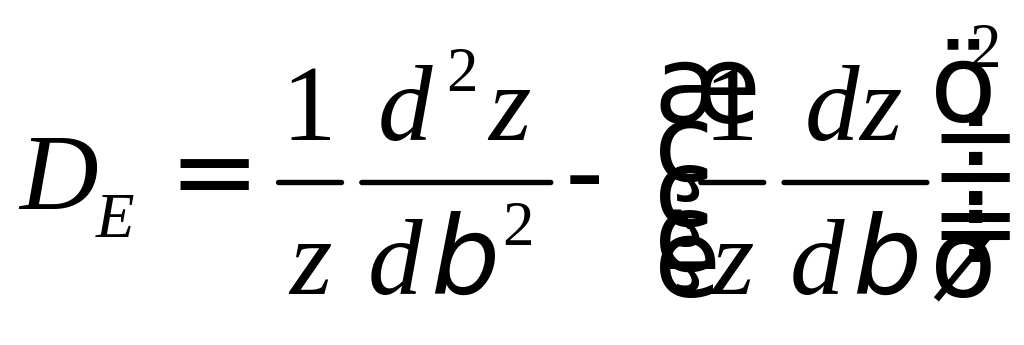 .
.
Однако:
![]()
![]()
![]()
![]() (при
(при
![]() )
)
Ответ:
![]() ;
При
;
При
![]() .
.
Задача 5. Найти дисперсию числа частиц в случае большого канонического распределения Гиббса.
Решение.
![]()
![]()
![]()
Видно, что
![]()
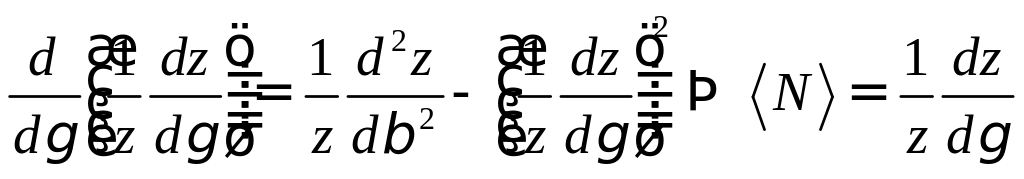
![]() ;
;
![]()
Ответ:
![]() ;
;
![]() .
.
Задача 6. Используя распределение
Гиббса:
![]() получить различные формы распределения
Максвелла:
получить различные формы распределения
Максвелла:
вероятность того, что скорость любой частицы заданной системы лежит в интервалах , , ;
вероятность того, что абсолютная величина скорости лежит в интервале ;
вероятность того, что кинетическая энергия любой частицы лежит в интервале ;
Решение: 1)
![]() ,
,
![]()
Так как
![]() ,
,
![]() ,
,
![]() статистически независимы, то:
статистически независимы, то:
![]()
Из условия нормировки:

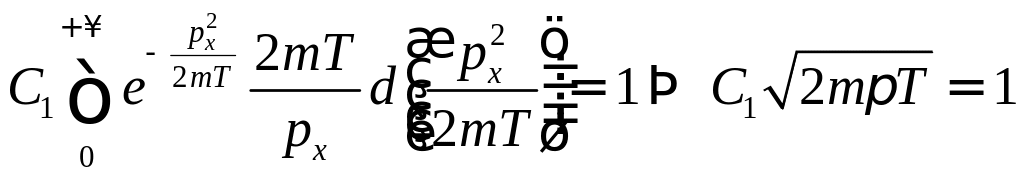
![]()
Аналогично:
![]() ;
;
![]() ;
;
Для нахождения
![]() перейдем к сферическим координатам:
перейдем к сферическим координатам:
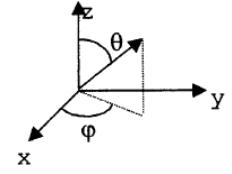
![]()
![]()
Найдем
![]() из
условия нормировки:
из
условия нормировки:
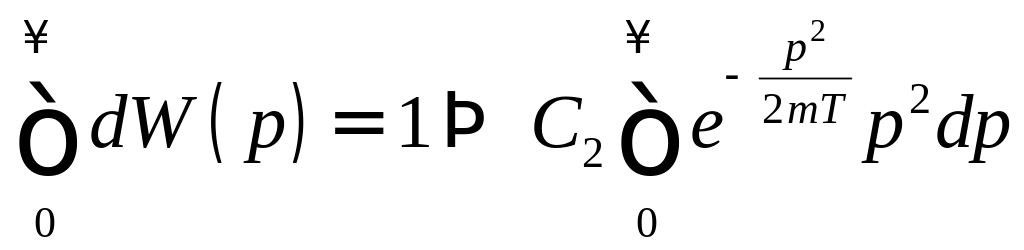
Сделаем замену переменных:
![]() .
Тогда
.
Тогда
![]() ;
;
![]()
![]() ,
,
где
![]()
Таким образом,
![]()
![]()
2)![]()
![]()
![]() ,
,
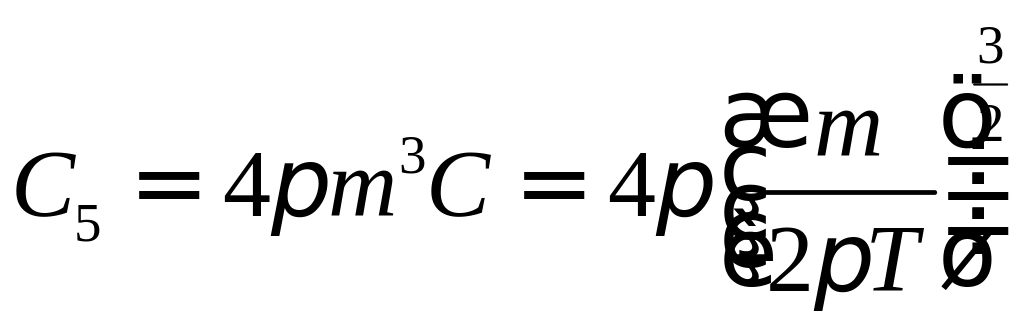
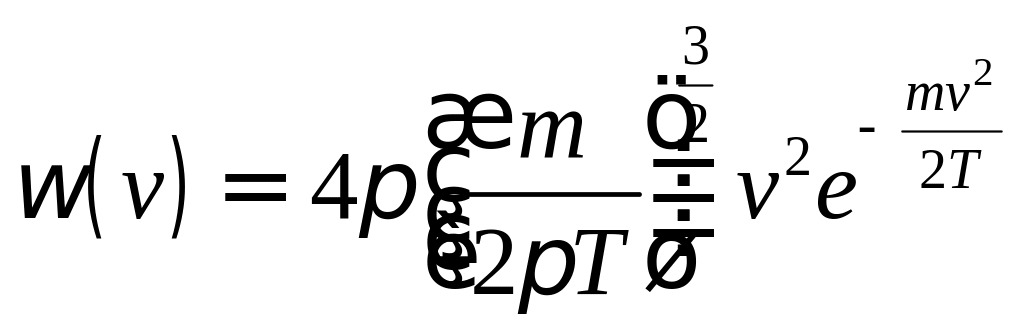
![]()
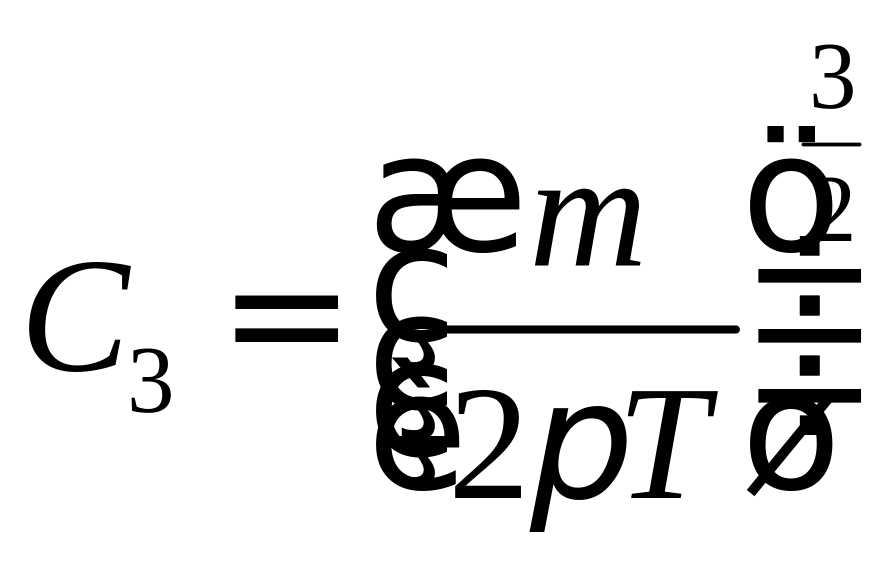 ,
где
,
где
![]()
![]() ,
где
,
где
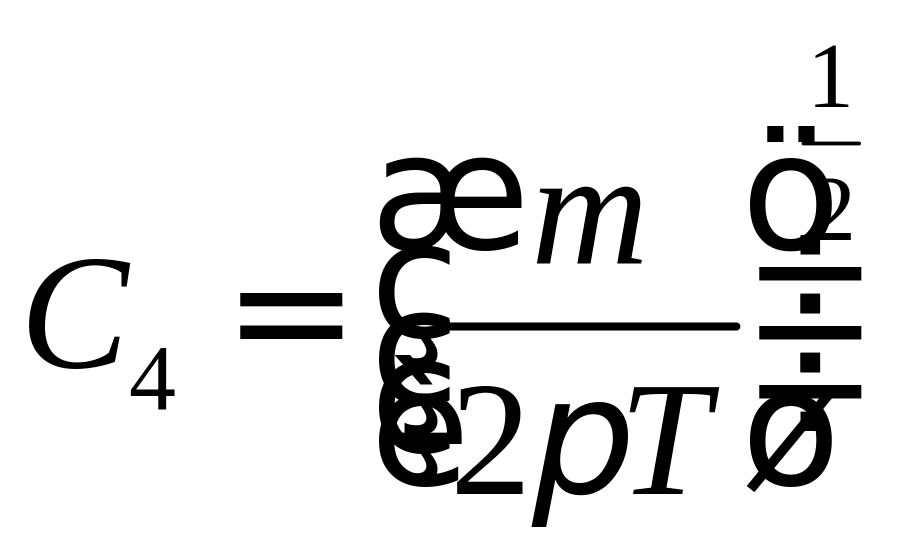
4)
![]()
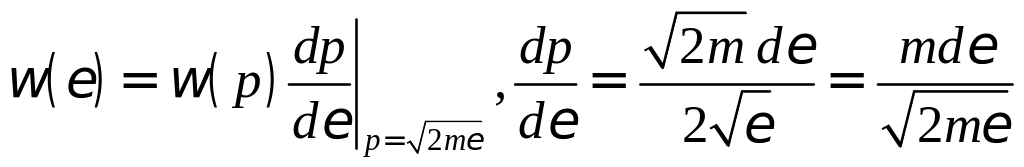
![]()
Ответ:
![]() ,где
,где
![]() ,
где
,
где
![]()
Задача 7. Используя распределение Максвелла, найти:
а) ;
б)![]() ;
;
в) (наиболее вероятное значение величины скорости);
Решение:
![]() ,
,
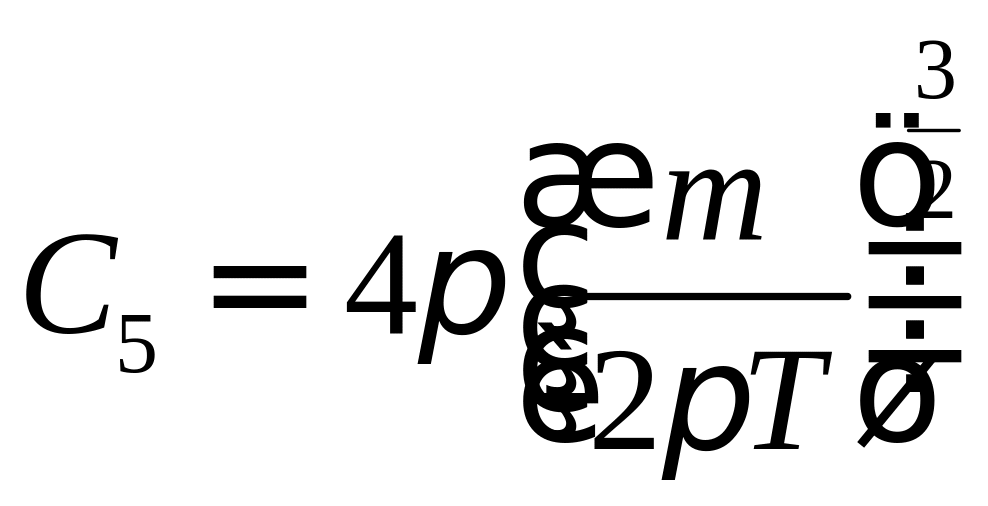
Сделаем замену переменных:
![]()
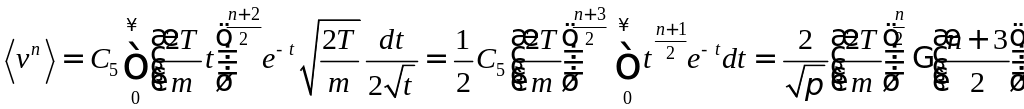
Если
-
четное![]() :
:
![]()
Если
-нечетное![]() :
:
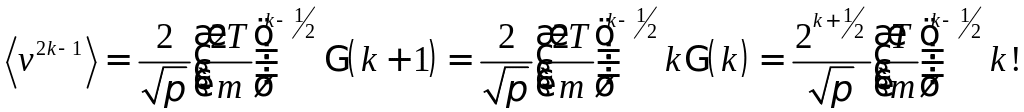
б)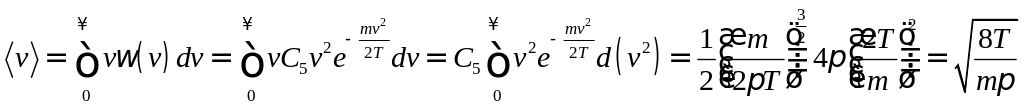 ,
,
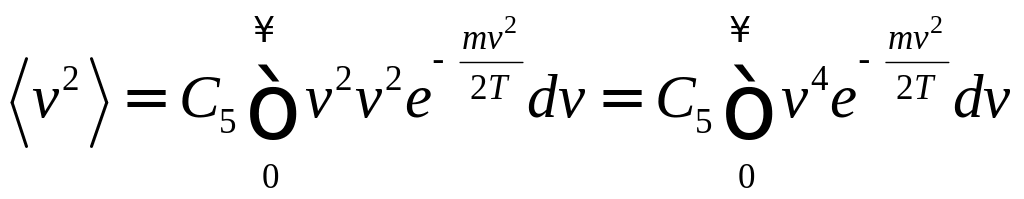
Сделаем замену переменных:
![]() ;
;
![]()
Тогда:
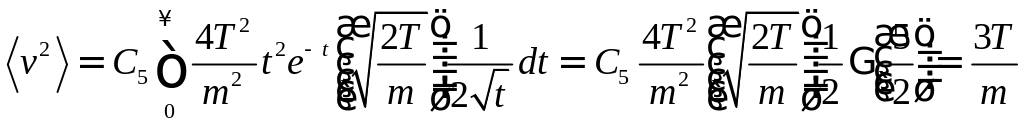
в) Ищем экстремум функции
![]() :
:

![]()
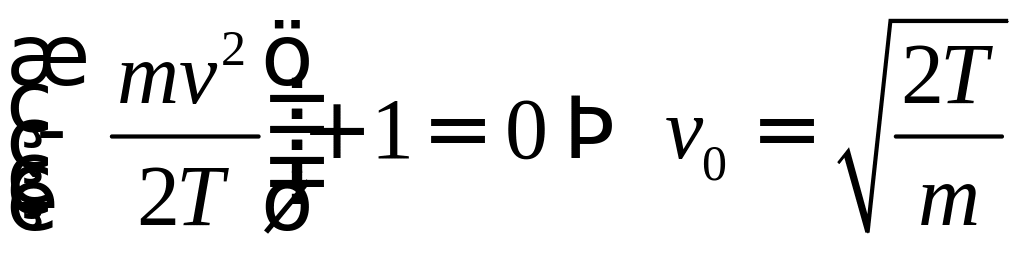
Ответ: Если
-четное
:
![]()
Если
-нечетное
:
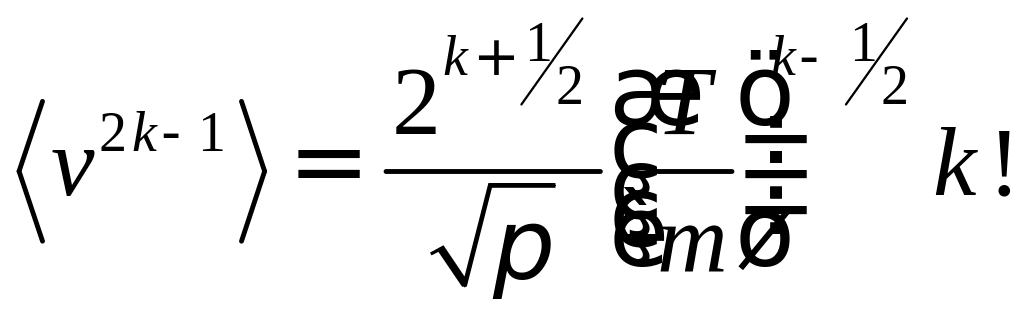
![]() ;
;
![]() ;
;
![]() ;
;
Задача 8. Используя распределение Максвелла, найти дисперсию скорости и среднее квадратичное отклонение .
Решение:
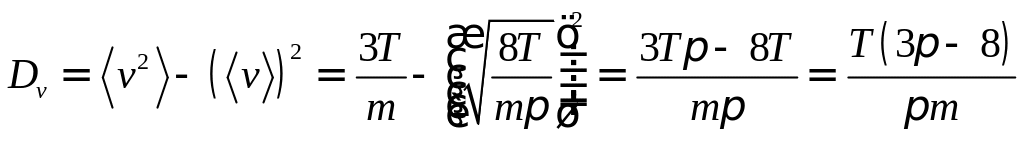
![]()
Задача 9. Найти и наиболее вероятное значение кинетической энергии частицы .
Решение: Условимся решать задачу в СГС (к=1).
![]() ,
где
,
где
![]()
Обозначим:
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]()
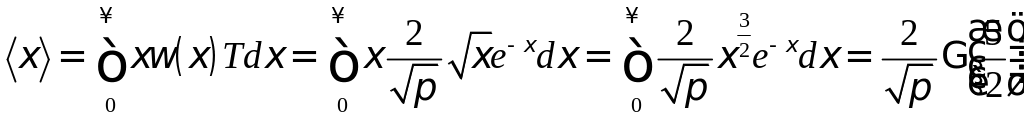
![]()
Найдем
как
экстремум функции
![]() :
:
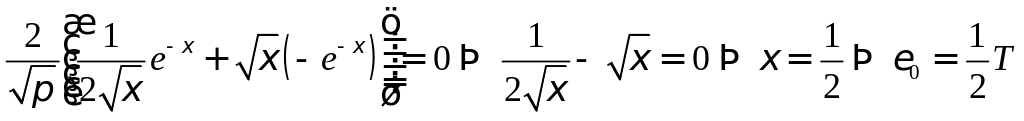
Ответ:
![]() ;
;
![]()
Задача 10: Используя распределение Максвелла, найти дисперсию кинетической энергии , где .
Решение:
![]()
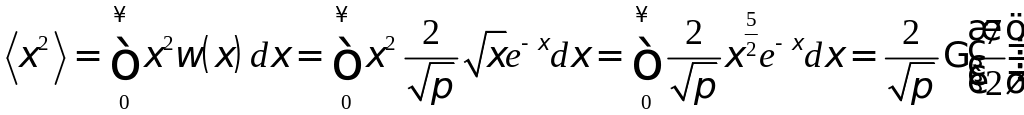
![]()
![]()
Задача 11. Найти вероятность того, что две частицы имеют абсолютную величину скорости относительного движения в интервале . Найти .
Решение: Условимся решать задачу в СГС (к=1).
Вероятность того, что 1 частица имеет
скорость
![]() ,
а вторая – скорость
,
а вторая – скорость
![]() :
:
![]()
Переходя к сферическим координатам:
![]()
Из условия нормировки найдем
![]() :
:
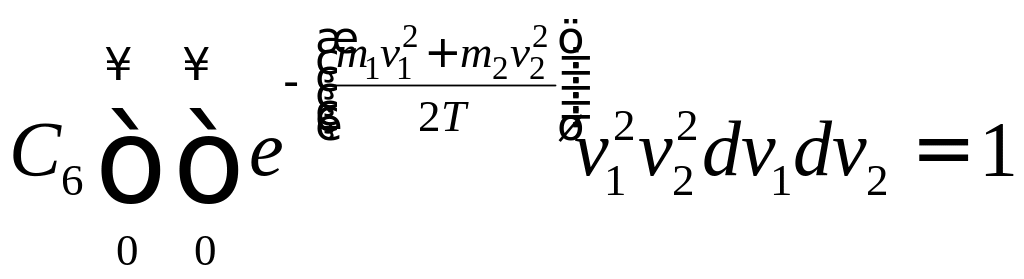

Сделаем замену переменных:
![]() ,
,
![]() ;
;
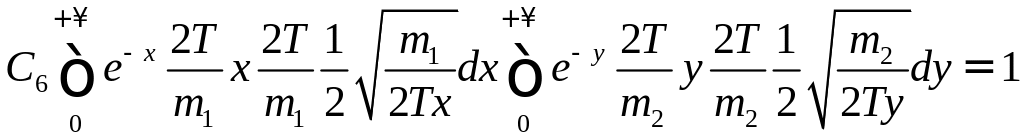
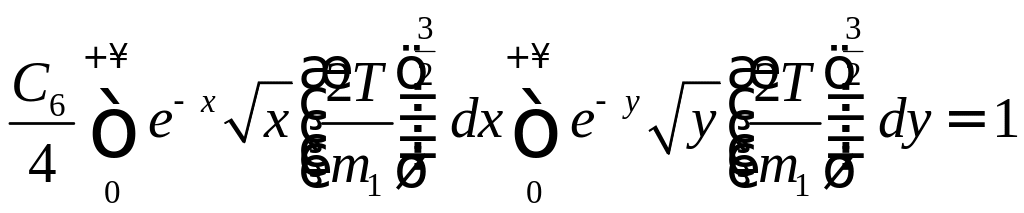
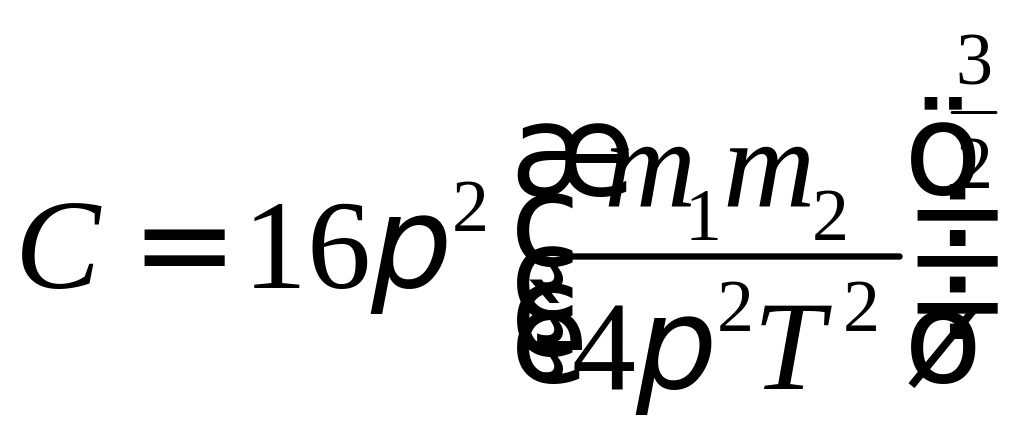
Перейдем к новым переменным: - относительная скорость;
![]() -
скорость центра масс;
-
скорость центра масс;
![]() - полная масса;
- полная масса;
![]() -
приведенная масса;
-
приведенная масса;
Учтем, что
![]() получим:
получим:
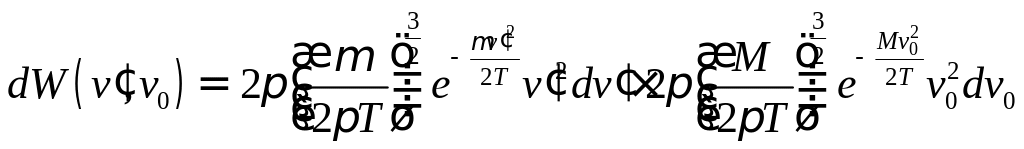
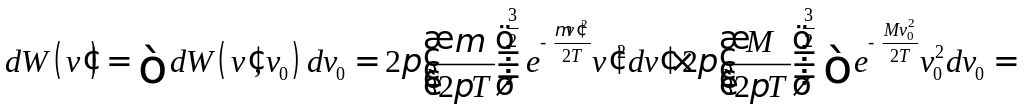
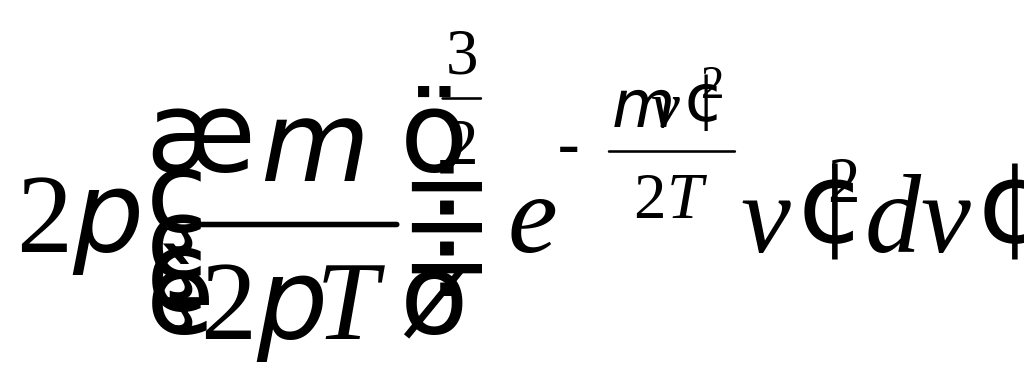
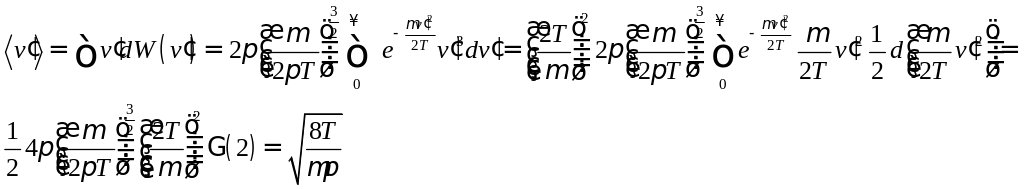
;
![]()
Ответ:
;
![]()
Задача 12. Используя распределение Гиббса, найти для идеального газа, помещенного во внешнее потенциальное силовое поле , вероятность того, что координаты любой частицы будут лежать в интервалах , , .
Решение.
![]()
Если
![]() (поле
тяжести)
(поле
тяжести)![]()
![]()
Число таких частиц в единице объема:
![]() .
.
Здесь
![]() ,
где интеграл находится в пределах
объема.
,
где интеграл находится в пределах
объема.
Ответ.
Задача 13. Найти центр тяжести столба идеального газа в однородном поле тяжести, если ускорение поля тяжести , масса молекулы , температура .
Решение. Воспользуемся предыдущей
задачей:
![]()
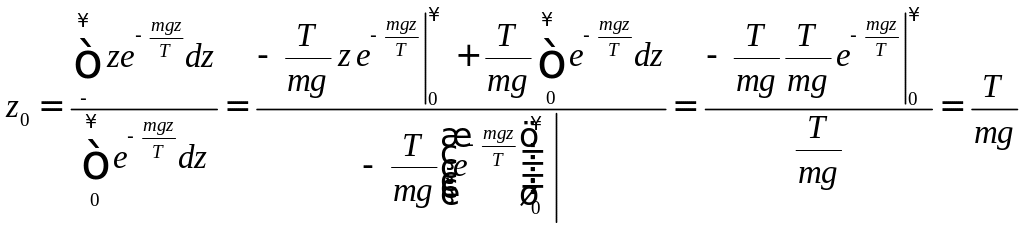
В СИ:
![]()
Ответ.
