§28. Расчёт импульса Ферми для электронного газа при

Будем пользоваться формулой:

Запишем функцию Ферми для электронного газа:

- он здесь как функция энергии

И рассматривается случай, когда очень близко к 0, :

, у нас

При малых показатель экспоненты отрицательный слева от и положительный справа от .

, при

Тогда

Поэтому:

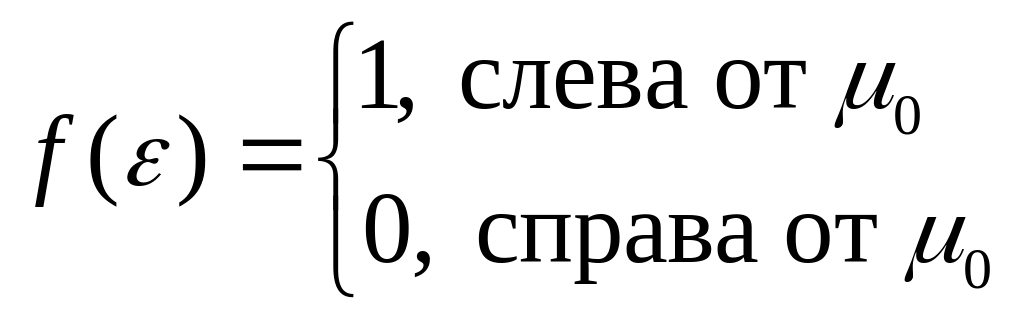
Видим, что имеет вид ступеньки: слева все уровни заселены, а справа все уровни свободны.

Химический потенциал определяется числом частиц в системе.

Можно писать

где - число частиц, а 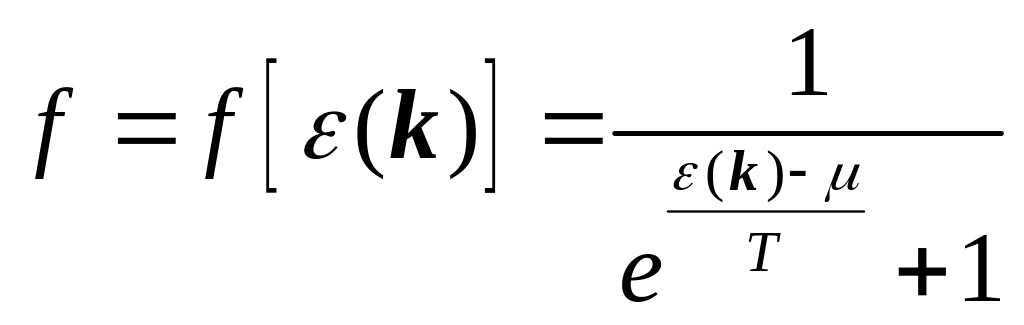- функция Ферми-Дирака, при она имеет вид ступеньки.

Запишем явный вид :

это выражение получается из выражения кинетической энергии электрона с импульсом :

,

Тогда всё сводится к интегрированию в -пространстве или в Фурье-пространстве. Размерность .

Пределы интегрирования в -пространстве:

Это шар с радиусом, который определяется . Радиус этого шара часто называют , т.е. -фермиевским.

определяется из , т.е. из числа частиц (электронов) в системе.

Полагаем объём и найдём полное число частиц в системе:

здесь из под интеграла убрали , т.к. в этом пределе интегрирования , а вне этого предела и интеграл тоже равен нулю.

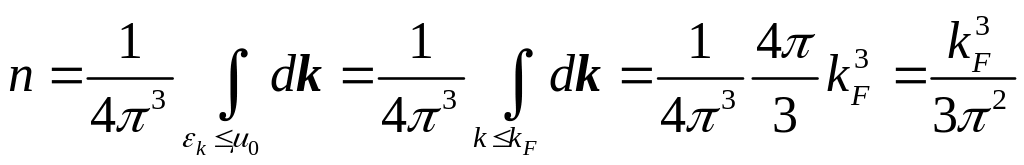
И тогда получаем:

Импульс Ферми:

Найдём :

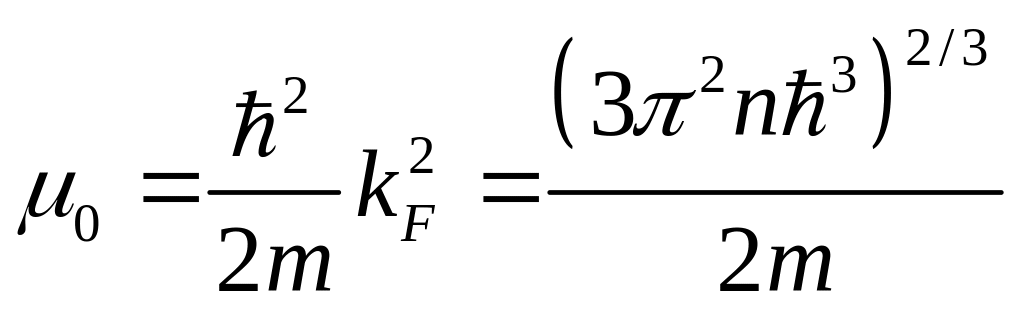
т.е. химический потенциал или уровень Ферми определяется концентрацией частиц.

§29. Расчёт энергии электронного газа при

- это полная энергия электронного газа.

где - средняя энергия, приходящаяся на один электрон.

Энергия имеет вид:

Тогда:

Найдём среднее :

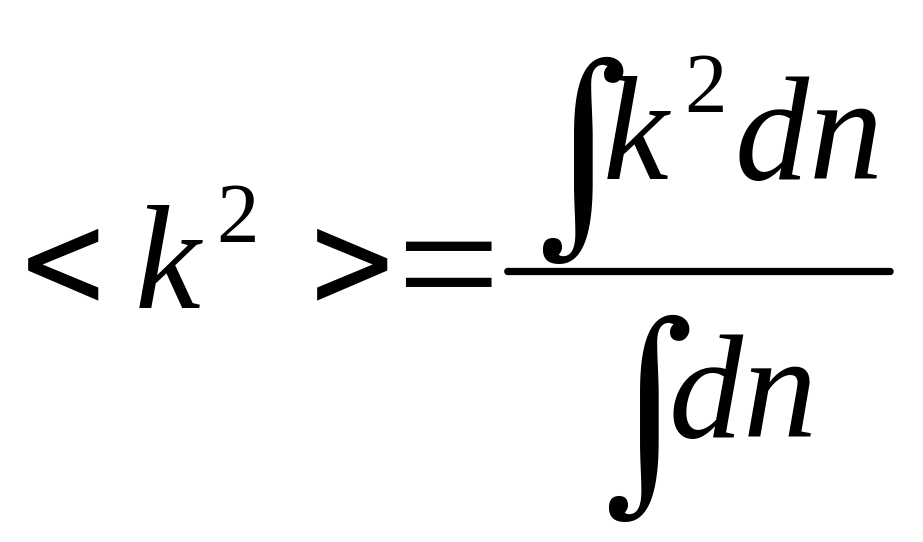
Учтём, что при область интегрирования является сферой, тогда:

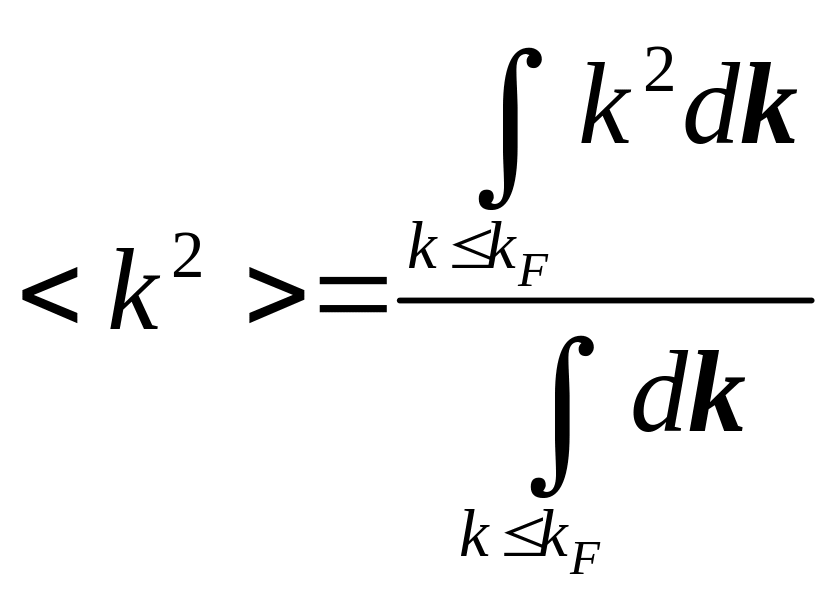
- это элементарный объём в -пространстве, т.е. скаляр, а не вектор.

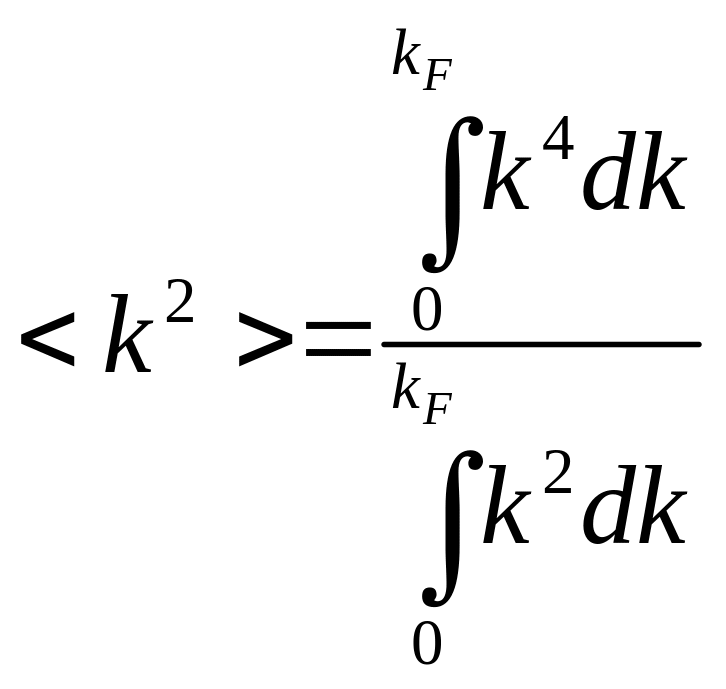
здесь мы уже сократили интегралы по углам, т.к. в числителе и в знаменателе они одинаковые: .

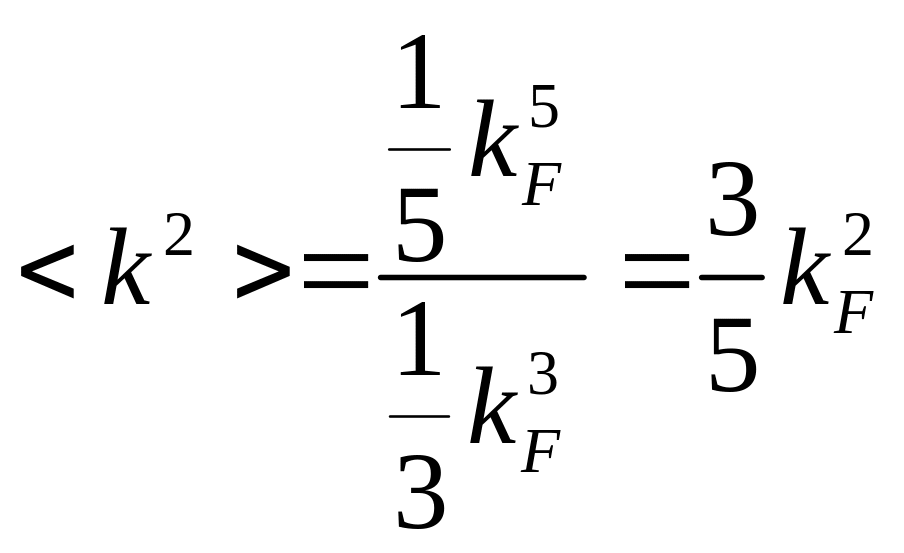
Но определяет энергию Ферми:

Значит:

Таким образом, полная энергия электронного газа при :

§30*. Уравнение состояния идеального электронного газа при . Критерий идеальности электронного газа

Чтобы записать уравнение состояния электронного газа при , вспомним соотношение между и для идеального газа:

Теперь в качестве подставим сюда :

(29)

Но ведь и мы получили, что всё зависит от концентрации. Соотношение (29) называется уравнением состояния идеального газа при .

Теперь рассмотрим критерий идеальности. Для больцмановского идеального газа писали критерий идеальности:

Для больцмановского газа

Для ферми газа

Мы оценивали энергию взаимодействия для электронного газа:

И видна принципиальная разница критериев идеальности для больцмановского газа и для ферми газа:

и видим такое различие:

для больцмановского газа

для ферми газа

Т.е. для ферми газа условие идеальности противоположно условию идеальности для больцмановского газа. Но в условии для ферми газа нет температуры – это не удивительно, т.к. у нас ферми газ при .

§31*. Числовые оценки параметров , , , , и

Начнём с концентрации. Рассчитаем концентрацию электронов в элементе ;

Здесь .Посчитаем концентрацию электронов для такой среды:

- число Авогадро, а - объём одного моля

где - атомный вес, - плотность железа.

Тогда

Рассчитаем :

Тогда радиус сферы Ферми:

- волновое число Ферми (так тоже называют).

Теперь оценим импульс Ферми.

,

Оценим скорость Ферми.

- скорость фермиевских электронов.

- т.е. релятивистские эффекты можно не учитывать

Посчитаем энергию Ферми:

Часто температуру Ферми измеряют в энергетической шкале, а бывает удобнее в градусах:

- в энергетической шкале

- в градусах

- постоянная Больцмана

С температурой связывают вырождение электронного газа. При комнатной температуре газ вырожденный.

Часто для описания вырожденного газа используют соотношения как для случая .