
- •Планирование и управление в условиях неопределенности и риска. Модели и методы интервального программирования
- •Элементы интервальной математики
- •Задачи интервального программирования с линейными ограничениями.
- •Модели ограничений.
- •Модели критерия.
- •Основы выпуклого анализа
- •Алгоритм проверки условия единственности оптимального решения задачи интервального программирования с интервальной целевой функцией.
- •Графическая иллюстрация.
- •Решение задач интервального программирования средствами Excel, Mathematica, MathCad
Алгоритм проверки условия единственности оптимального решения задачи интервального программирования с интервальной целевой функцией.
Сформировать матрицу
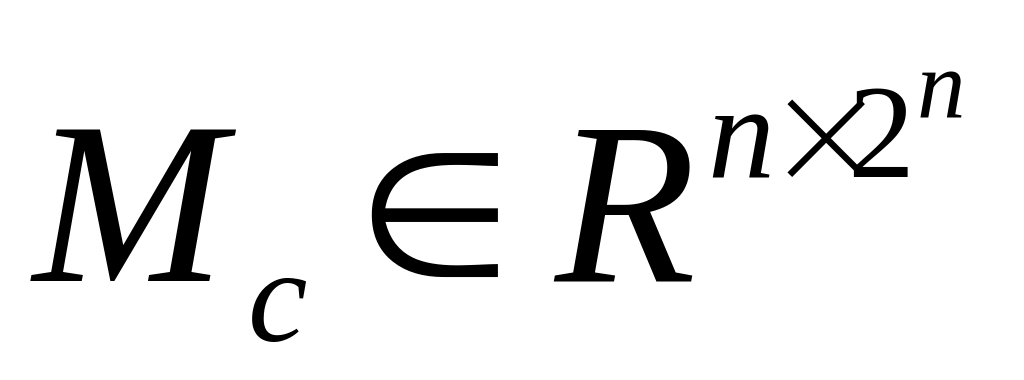 из
векторов
из
векторов
 ,
задающих вершины гиперпараллелепипеда
,
задающих вершины гиперпараллелепипеда
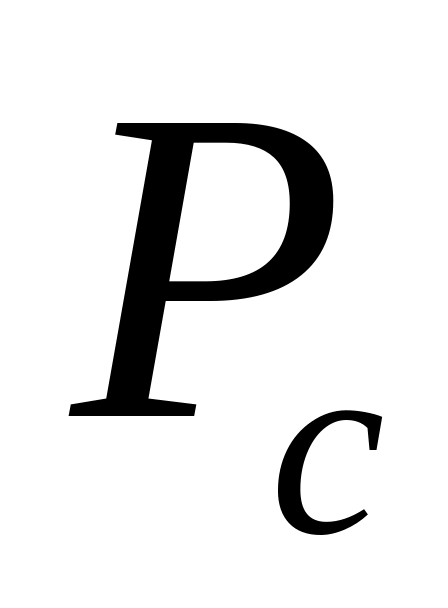 :
:
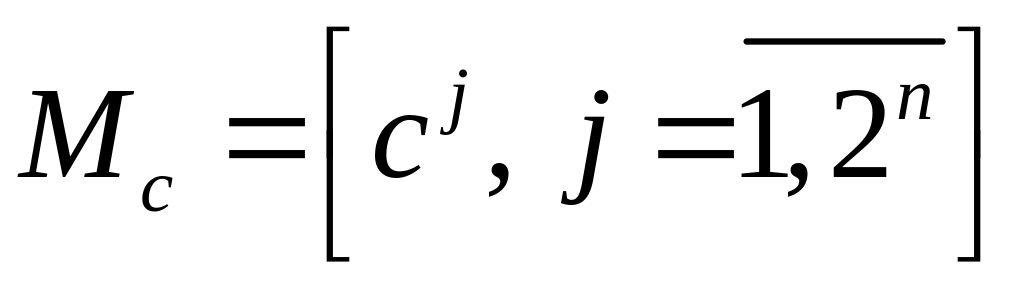 .
Матрица
.
Матрица
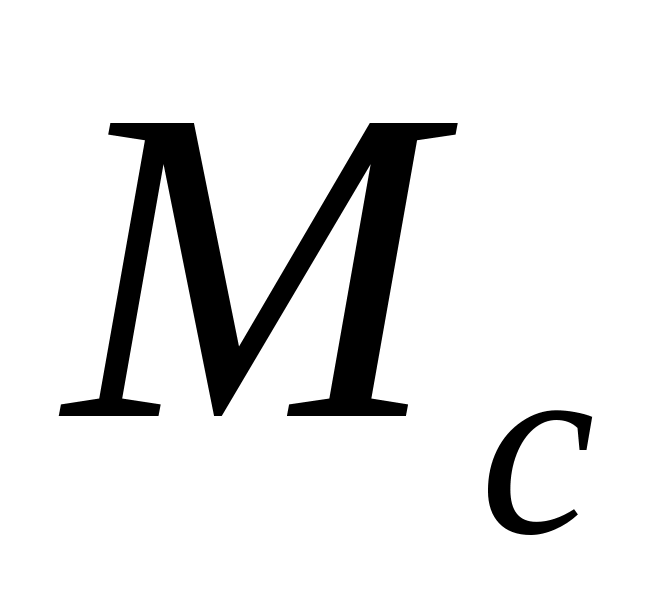 определяет конус
определяет конус
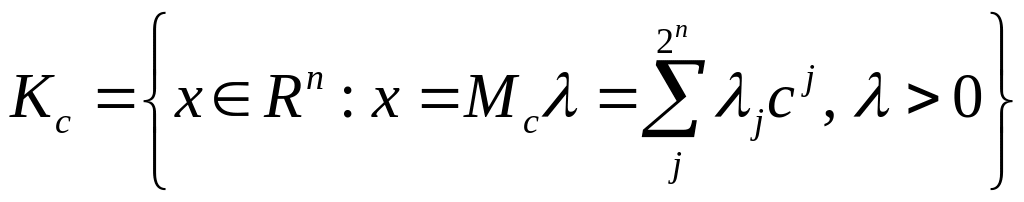 .
.Берем первый столбец и находим решение задачи с этим столбцом в качестве градиента
![]() ,
,
-
нашли точку
![]() .
.
В точке формируем матрицу
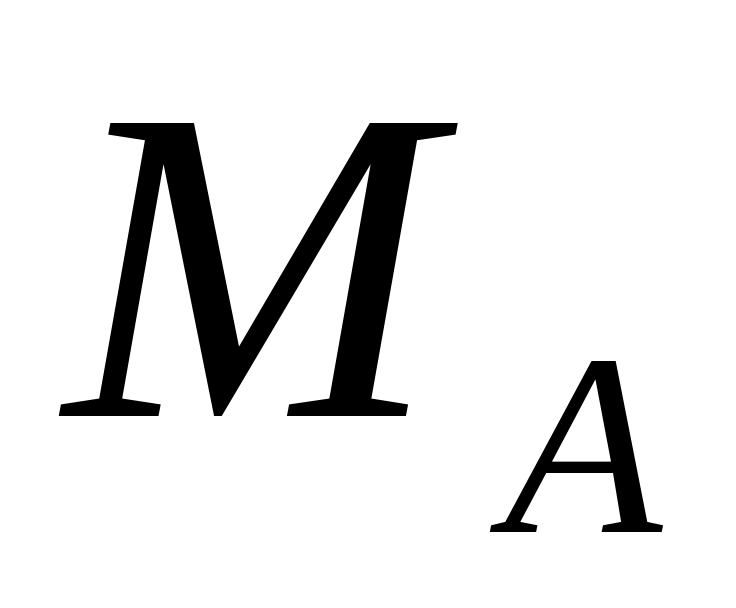 ,
столбцы которой - векторы нормалей
активных ограничений (гиперплоскости
,
столбцы которой - векторы нормалей
активных ограничений (гиперплоскости
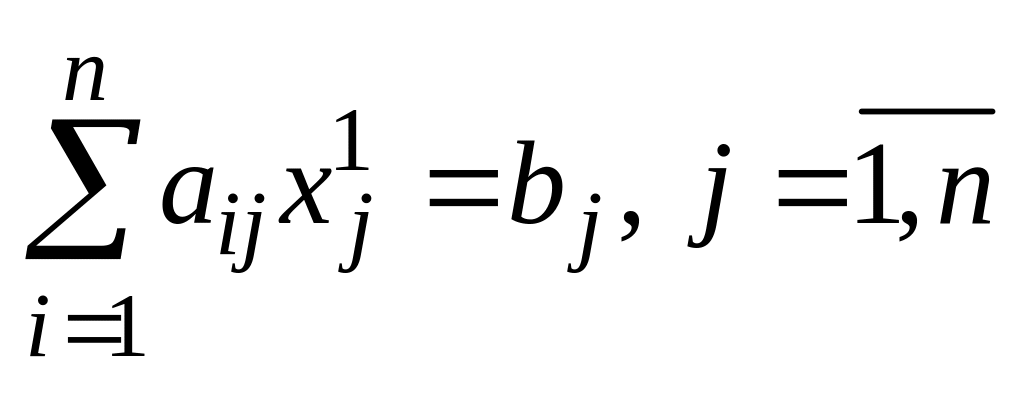 ).
Она задает конус
).
Она задает конус
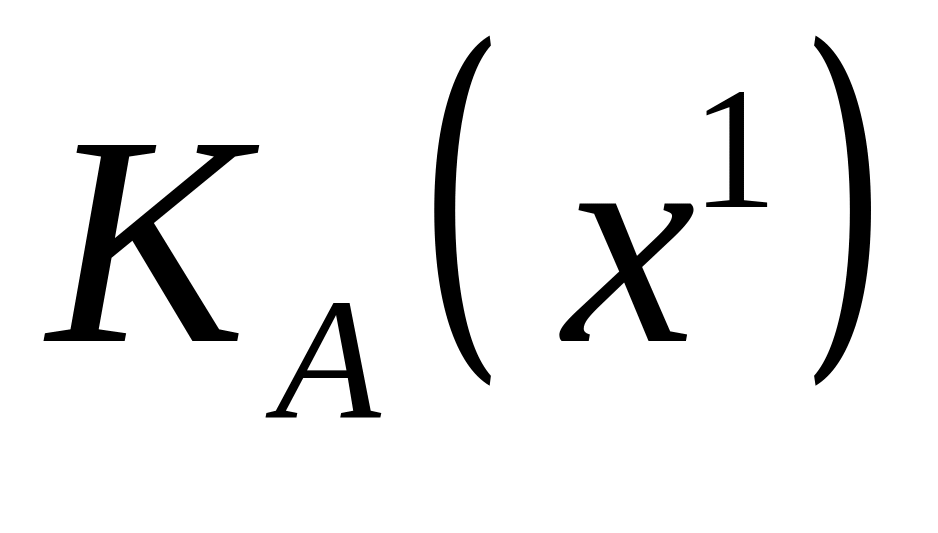 .
.Решаем матричное уравнение
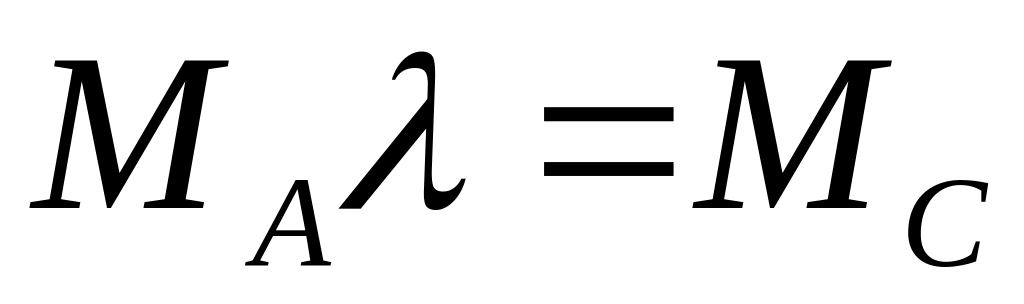 относительно матрицы
относительно матрицы
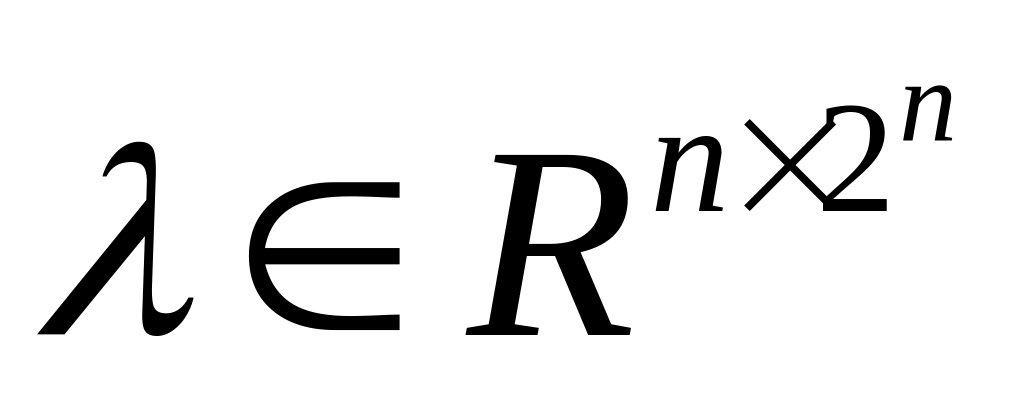 .
.Если
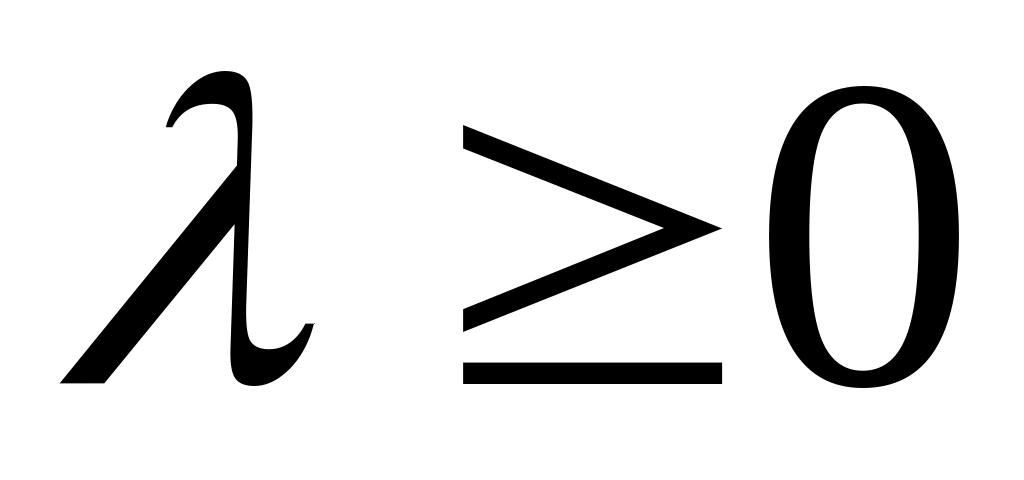 ,
то
лежит
в
,
то
лежит
в
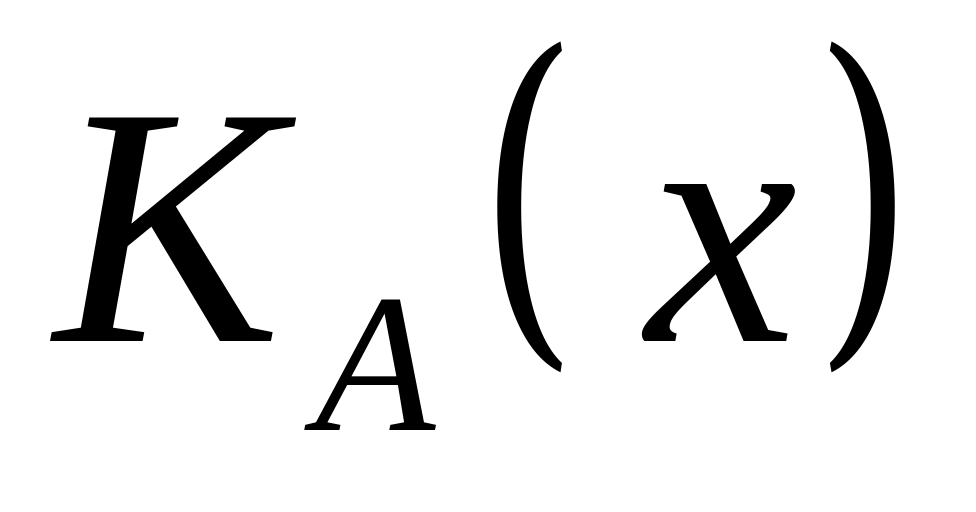 ,
то
- единственное решение.
,
то
- единственное решение.Если
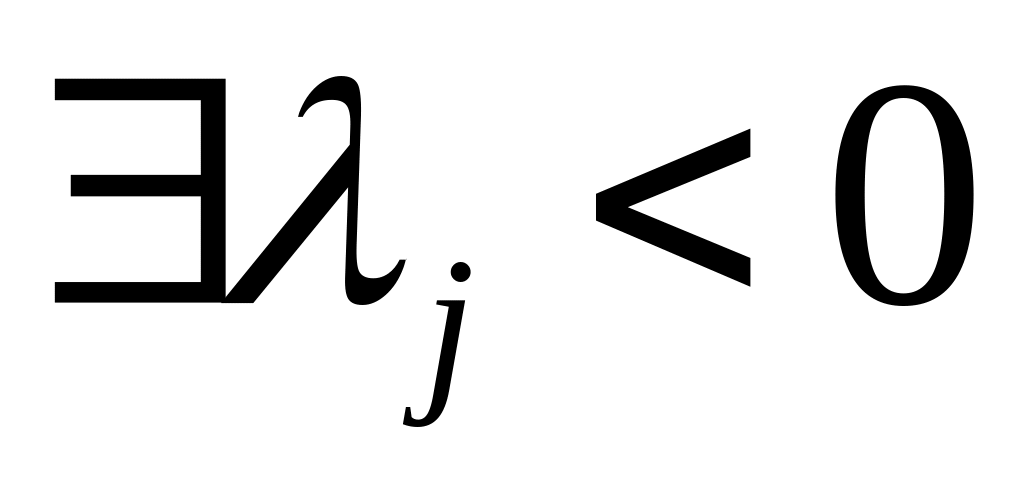 (это означает, что соответствующие
векторы
(это означает, что соответствующие
векторы
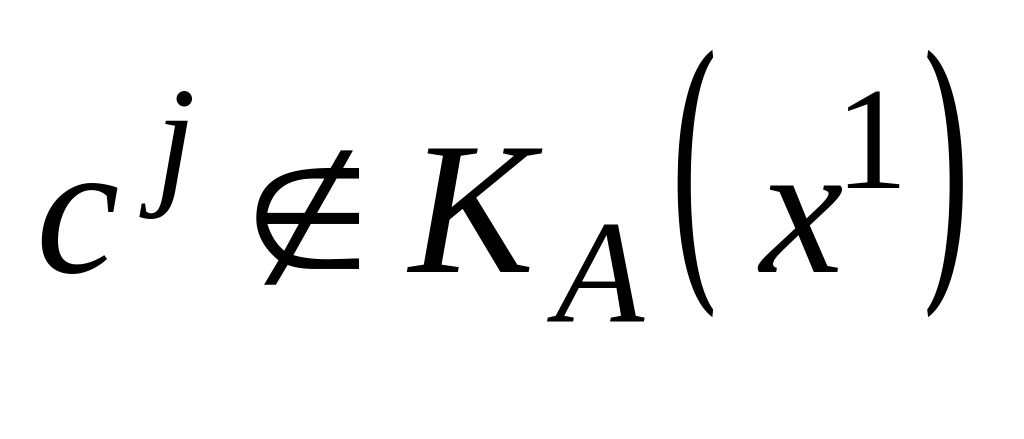 ,
следовательно
,
следовательно
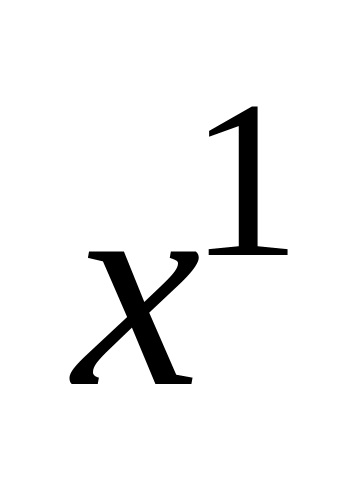 неединственное), то для определения
множества недоминируемых решений
выбираем шаг 7.
неединственное), то для определения
множества недоминируемых решений
выбираем шаг 7.
Примечание.
Если среди
![]() есть отрицательные, но они соответствуют
только ограничениям равенствам, то
решение единственно.
есть отрицательные, но они соответствуют
только ограничениям равенствам, то
решение единственно.
Выбираем поочередно столбцы матрицы и выполняем шаги начиная со 2.
В
результате найдем все граничные точки
множества
![]() -
множество эффективных и недоминируемых
решений.
-
множество эффективных и недоминируемых
решений.
Пример оптимизации режима обжатия заготовки.(см. лабу)
Решение задач интервального программирования средствами Excel, Mathematica, MathCAD.(см. лабу)
Графическая иллюстрация.
Решение задач интервального программирования средствами Excel, Mathematica, MathCad
