Планирование и управление в условиях неопределенности и риска. Модели и методы интервального программирования

Следует повторить

• определение выпуклого множества, конуса, выпуклого конуса,

• необходимое и достаточное условие выпуклости конуса, определение крайнего вектора для выпуклого конуса, конической оболочки, многогранного конуса.

• Нормаль

• Активные, пассивные ограничения

• Правила сравнения интервалов

Элементы интервальной математики

Обозначим

[b]=[b^-,b⁺] - числовой интервал,

[b] – интервальная переменная,

[f(x)]={f^-(x)<= f(x)<=f⁺(x)} - интервальная функция,

[A]=([a_ij]) – интервальная матрица.

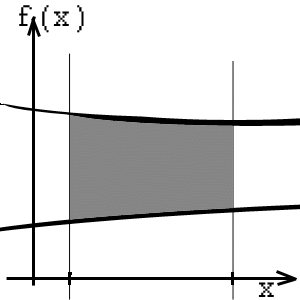
Здесь - неизвестная функция, - известные точно заданные границы коридора ее возможных значений.

Пример: f(x)]=[-1,1]+[0.5,1]x; f^--(x)=min{[-1,1]+[0.5,1]x}, f⁺(x)=max{[-1,1]+[0.5,1]x}.

Варианты описания интервальной функции см. в рукописи.

• С заданной абсолютной ошибкой

• С заданной относительной ошибкой

• Параметрическая модель с интервально заданными коэффициентами

При умножении интервала на меняется знак границ интервала и сами границы меняются местами:

Задачи интервального программирования с линейными ограничениями.

Пусть неизвестны точные значения параметров порождающей задачи линейного программирования и возможным реализациям этих параметров нельзя приписать функцию распределения внутри известных границ.

Задача интервального программирования имеет вид:

Модели ограничений.

Рассмотрим возможные модели допустимой области

X1 – самая жесткая постановка, X4 – наиболее «либеральная».

Учитывая неотрицательность переменных x>=0, можно выразить множества Xi через граничные элементы интервальной матрицы [A] и интервального вектора [b] (получить детерминированные эквиваленты моделей ограничений)

X₅={x>=0: x<= }, где =(b⁺+b^-)/2

Из анализа экстремальных допустимых областей следуют включения:

.

Пример.

Приведенные выражения позволяют, используя содержательную интерпретацию и технологические требования к допустимому решению определить детерминированную допустимую область задачи в форме одного из множеств , уже не охватывающего интервально заданные параметры.

Модели критерия.

В качестве целевой функции можно взять любую функцию, удовлетворяющую условию

. (*)

Ее вид зависит от специфики оптимизируемой системы и информации о виде функции.

Утверждение 1. При любом выборе f(x) согласно условию (*) вариация экстремального значения критерия ограничена пределами

, (1*)

где .

Доказательство. Для выполнено (*). Покажем, что

min f(x) = f(x₀)<= f⁺(x₀⁺)=min f⁺(x).

От противного. Пусть выполнено обратное:

min f(x) > min f⁺(x),

Тогда для f(x) > min f⁺(x)= f⁺(x₀⁺). Возьмем x=x₀⁺: ­ f(x₀⁺)>f⁺(x₀⁺), что противоречит (*). Значит, (1*) верно. Аналогично доказывается f(x₀^-)<= f(x₀). Утверждение доказано.

Рис. Иллюстрация к утверждению 1.

Упражнение. Сформулируйте и докажите аналог утверждения 1 для задачи на максимум.

Возможные варианты модели критериев:

1 MaxMin модель (пессимистический подход). Применяется, когда необходимо обеспечить гарантированный результат:

max f(x)->min, f [f(x)], x X, X₁={x>=0: A,b Ax<=b}.

Эта постановка ориентирована на наихудший случай, особенно в случае допустимой области

2 MinMin модель (оптимистический похдход), (минимальная из возможных моделей критериев):

minf(x)->min, f [f(x)], x X, X₄={x>=0: A [A], b [b] Ax<=b}.

Если использовать область , то буде получено минимально возможное значение критерия.

3 постановка в среднем: ,

Наиболее естественно использовать Х_5.

4. многокритериальная задача: f₁(x)->min, … , f_m(x)->min, f_i(x) [f(x)]. Далее можно использовать любые методы решения многокритериальной задачи.

Добавить из рукописи