5. Интерпретация для исходной задачи полученного (по детерминированному эквиваленту ( Максиминная модель с ограничениями (х3).) решения

При любом варианте реализации функции расхода топлива (модели парогенератора) расход топлива не превысит . Оптимальная производительность первого парогенератора равна 170, второго – 100 т/ч. При этом, каким бы ни было реальное потребление энергии ( ), потребность в ней будет удовлетворена полностью ( ).

Добавить решение модели в среднем с ограничениями в среднем

Интерпретация для исходной задачи полученного (по детерминированному эквиваленту модели в среднем с ограничениями в среднем) решения

Минимальный средний расход топлива равен ……при производительности парогенератора…(170, 100).

Пример задания №2

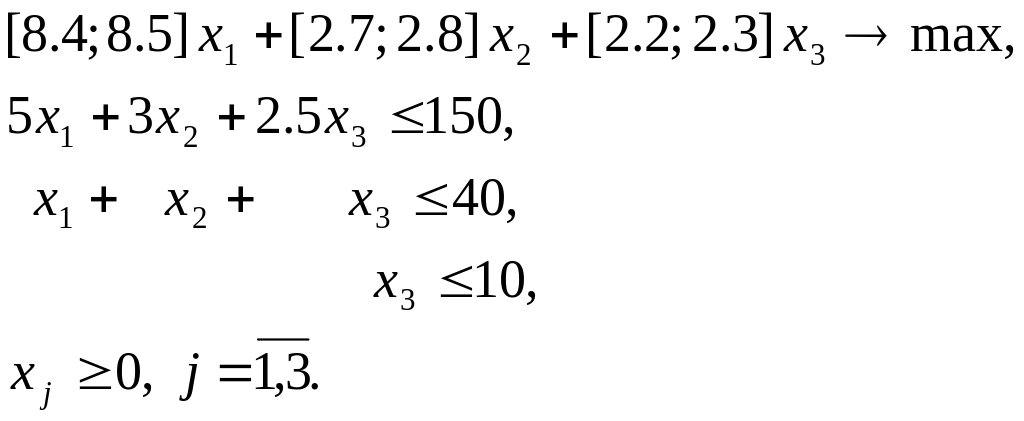
Решение задачи №2

1.Детерминированный эквивалент (минимаксная модель).

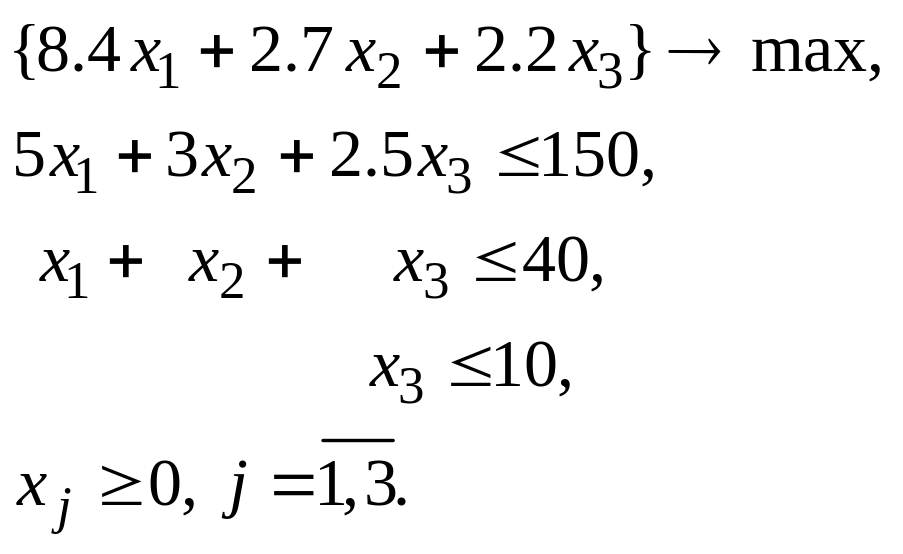равносильно

2. Решение задачи: .

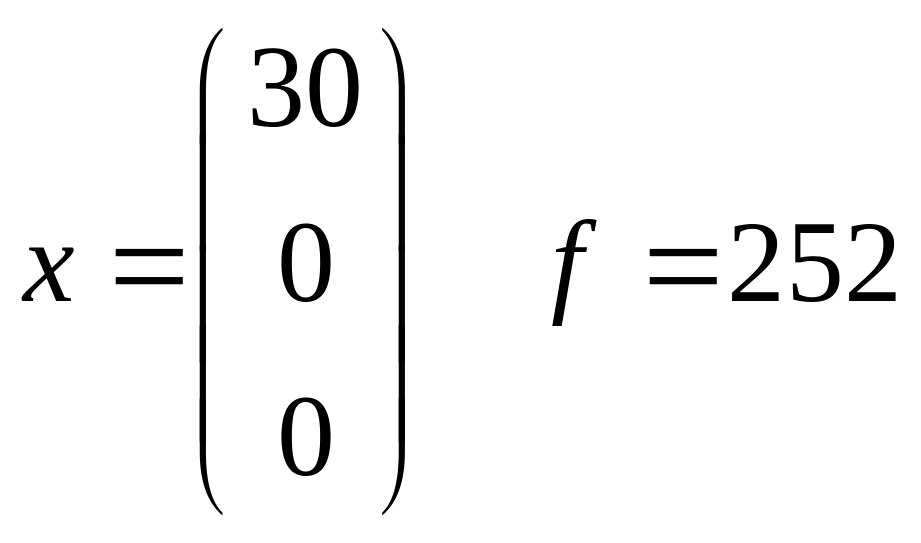Maximize[{8.4x1+2.7x2+2.2x3,5x1+3x2+2.5x3150,x1+x2+x340,x310,x10,x20,x30},{x1,x2,x3}]

{252.,{x130.,x20.,x30.}}

3. Проверка единственности решения.

3.1 Сформируем матрицу из векторов :

3.2 Формируем ЗЛП с коэффициентами из первого столбца :

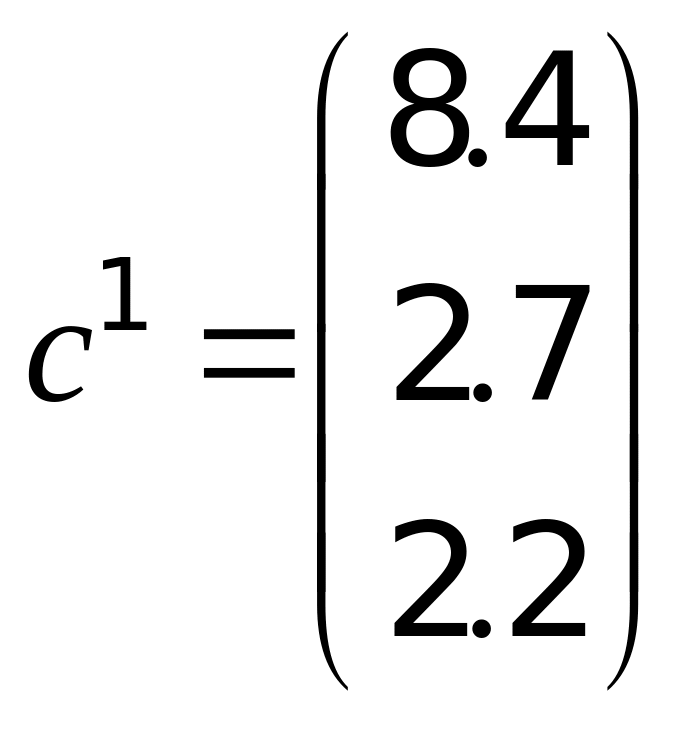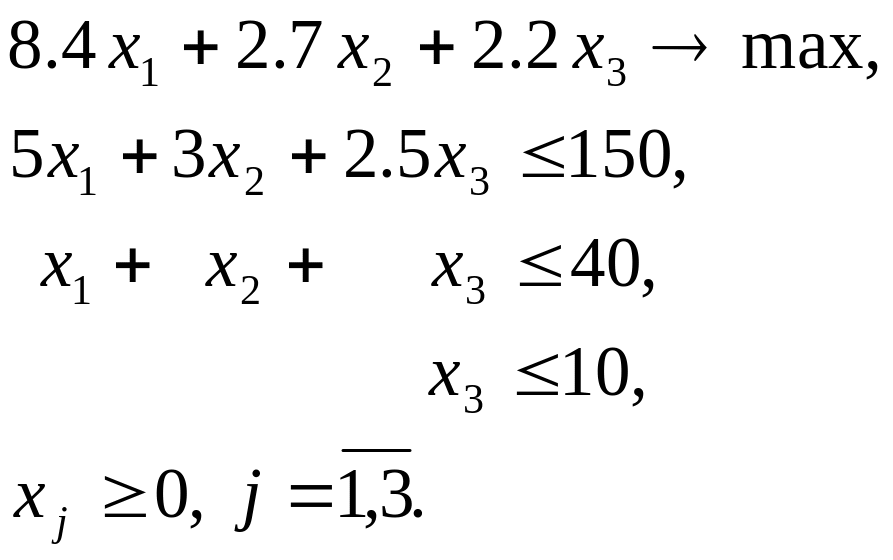
Вектору соответствует оптимальный план:

Активными в точке являются первое, пятое и шестое ограничения.

3.3. Для решения формируем матрицу , столбцы которой – векторы нормали активных ограничений в точке :.

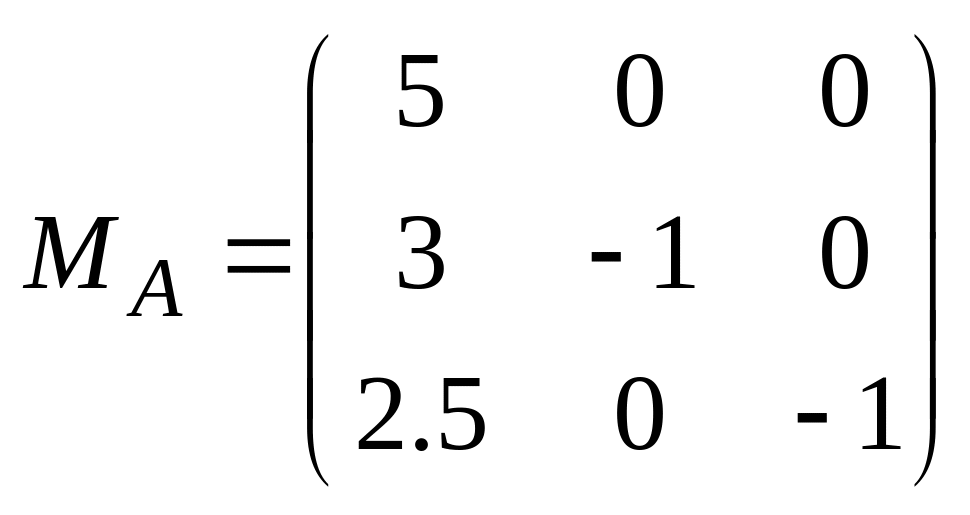
3.4. Решаем матричное уравнение :

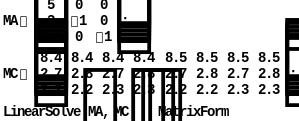
3.5. Т.к. все , то - единственное решение задачи №2.

4. Полученный результат говорит о том, что оптимальный технологический режим обжатий нечувствителен к изменениям коэффициентов целевой функции (т.е. линейных деформаций заготовки) в заданных пределах.

Решим задачу с измененными условиями:

Постановка задачи №2

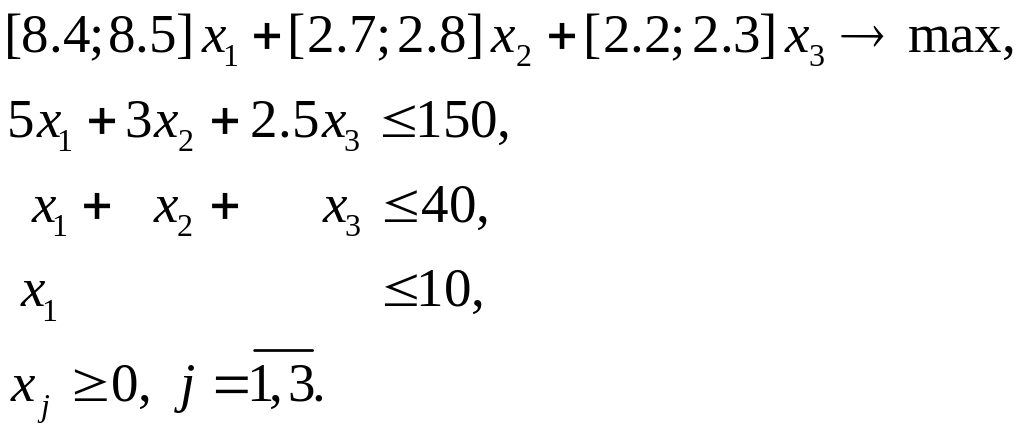
Решение

1.Детерминированный эквивалент (минимаксная модель).

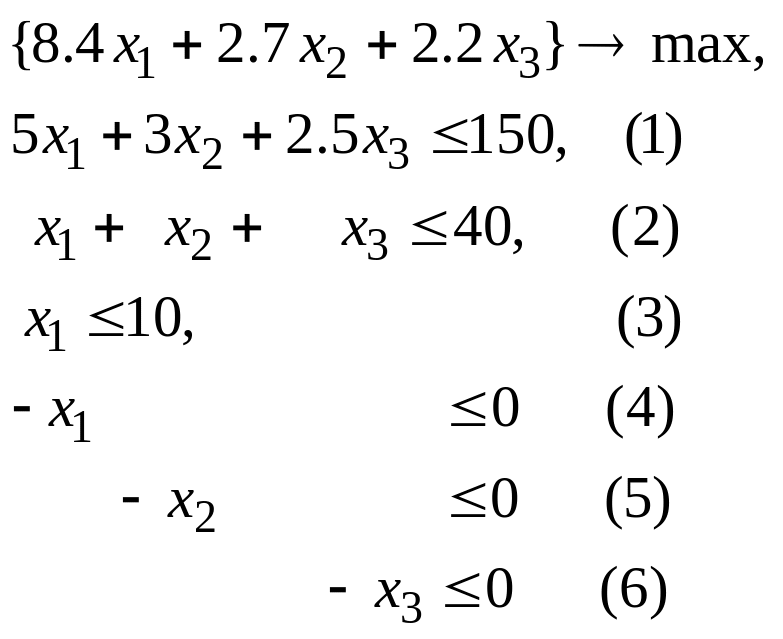
2. Решение задачи:.

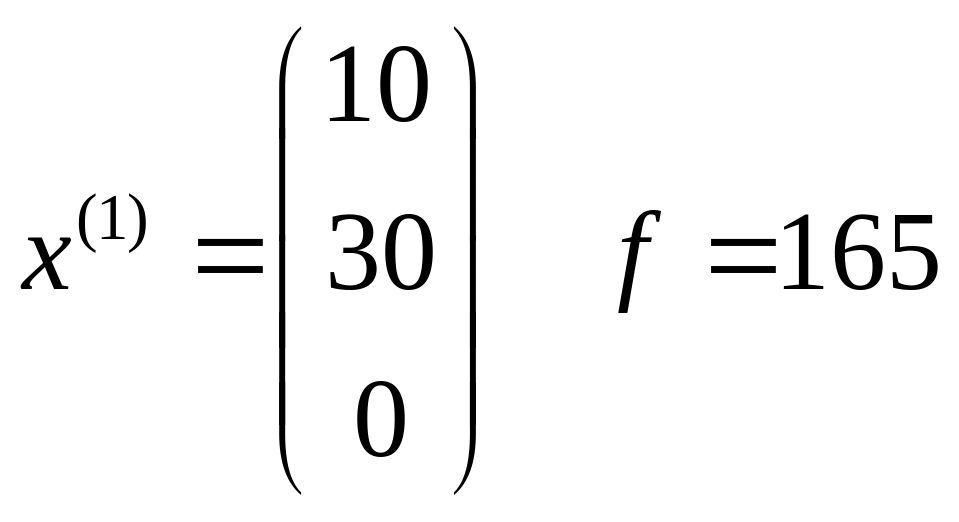
Maximize[{8.4x1+2.7x2+2.2x3,5x1+3x2+2.5x3150,x1+x2+x340,x110,x10,x20,x30},{x1,x2,x3}]

{165.,{x110.,x230.,x30.}}

3. Проверка единственности решения.

3.1 Сформируем матрицу из векторов :

Активными в найденной точке являются первое, второе и шестое ограничения.

3.3. Для решения формируем матрицу , столбцы которой – векторы нормали активных ограничений в точке :.

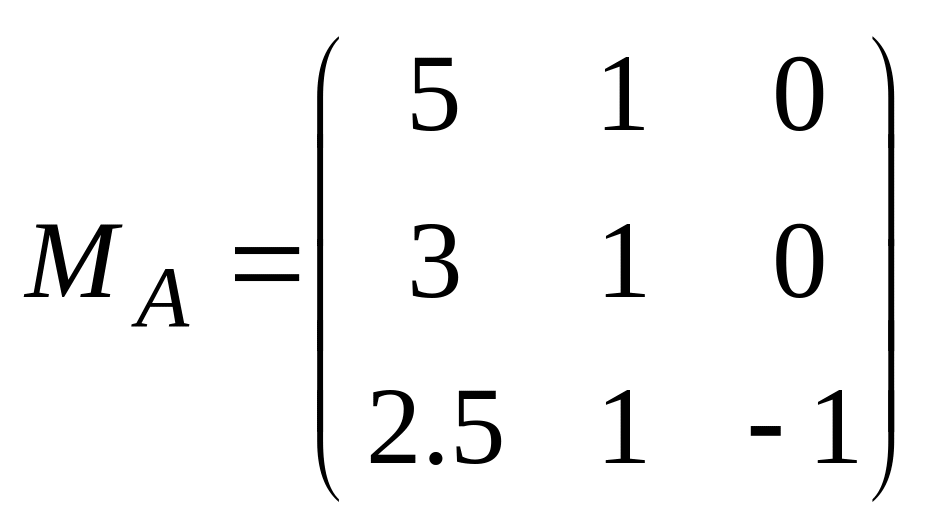
3.4. Решаем матричное уравнение :

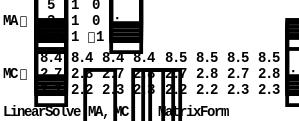
3.5. Т.к. есть , то - неединственное решение задачи №2.

4. Полученный результат говорит о том, что оптимальный технологический режим обжатий чувствителен к изменениям коэффициентов целевой функции (т.е. линейных деформаций заготовки) в заданных пределах.

Далее надо найти недоминируемые решения

Пример задания №3

Рассмотрим задачу линейного интервального программирования (1)

с параметрами (2) [A] = [ ] = ; [b] = [ ] = ; [c] (**)

Задача для нахождения ε -плана задачи (1) с параметрами (**) (задача (4)):

2x₁-x₂→max

-7x₂ – ε ≤ -3

-4x₁ + 4x₂- ε ≤ -4

2x₁ + 11x₂- ε ≤ 1

10x₁ - 2x₂- ε ≤ 0

x_1,x₂>=0, ε >= 0

Решим данную задачу графически, с заданным ε .

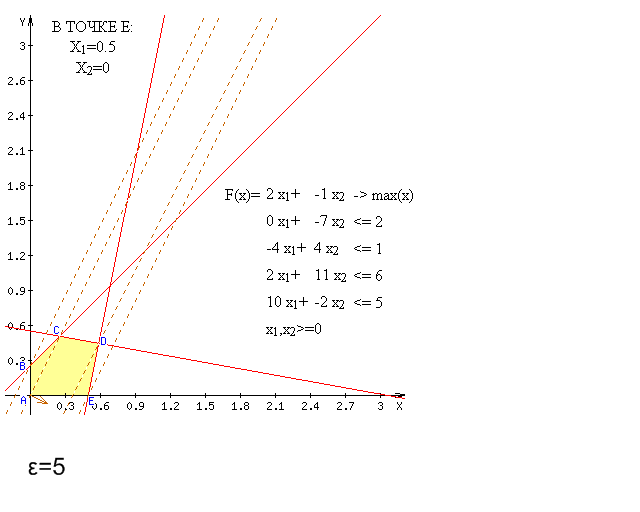
Норма невязки

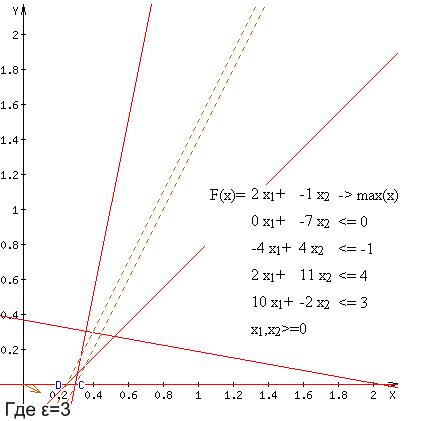
Таким образом, для примера 1 решены две задачи семейства (4).

Найдем оптимальную невязку и множество универсальных планов для задачи интервального программирования из примера 1.

Задача вычисления минимальной нормы невязки для примера 1 имеет вид

-7x₂ – ε ≤ -3

-4x₁ + 4x₂- ε ≤ -4

2x₁ + 11x₂- ε ≤ 1

10x₁ - 2x₂- ε ≤ 0

Здесь , - неизвестные, е – m -вектор с единичными координатами - , - сумма координат (норма) невязки .

Решая задачу симплекс-методом получаем ответ:

x*=

минимальная норма невязки равна

ВСТАВИТЬ РЕШЕНИЕ ЗАДАЧИ (4) С НАЙДЕННЫМ ОПТИМАЛЬНЫМ епсилон – множество универсальных планов

Чтобы найти среди всех универсальных планов наилучший по целевому условию (4), рассмотрим задачу линейного программирования (6).

2x₁-x₂→max

-7x₂ – ε ≤ -3

-4x₁ + 4x₂- ε ≤ -4

2x₁ + 11x₂- ε ≤ 1

10x₁ - 2x₂- ε ≤ 0

Где неизвестные x₁, x₂, .

Решая задачу симплекс-методом получаем ответ:

оптимальный план

Таким образом, наиболее «приемлемым» решением для всего параметрического семейства задач линейного программирования, порождаемых допустимыми реализациями исходных данных для примера 1, является универсальный план , соответствующая минимальная невязка составляет . При этом наилучший гарантированный результат целевой функции составит .

Еще решить через детерминированный эквивалент с постановкой согласно варианту.

Сравнить решения с постановкой