Вопрос 15. Полные метрические пространства

Вспомним материал первого семестра. Мы доказали там критерий Коши существования предела последовательности :

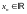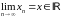
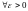
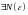
существует 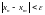. (это свойство называлось фундаментальностью последовательности).

Тогда же мы отметили, что если рассматривать 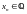, то полученный предел 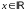может не принадлежать (т.е. может оказаться иррациональным числом). Это свойство мы отметим, как полноту 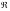и неполноту , соответственно. Мы также отметим, что служит для пополнением (подразумевая пополнение по метрике .

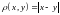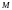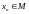Рассмотрим теперь произвольное метрическое пространство с расстоянием и назовем последовательность фундаментальной , если 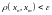(Также последовательности называют также последовательностями Коши)

Теорема 1. Если существует 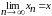; 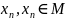, то 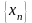- фундаментальная последовательность

Пусть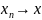 . Тогда .

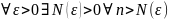
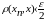Но тогда



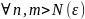
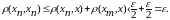
Определение . Множество точек метрического пространства называется ограниченным, если оно целиком содержится в некотором шаре этого пространства М.

Можно сформулировать это определение в равносильном виде: Для любой точки 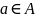множество расстояний 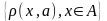представляет собой ограниченное сверху числовое множество (ограниченность этого множества снизу очевидна: ).

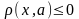Теорема 2. Если последовательность фундаментальна, то множество ее значений – ограниченное множество в .

Положим =1 и рассмотрим определение фундаментальности, согласно которому существует N=N(1) такие, что для всех n, m>N(1) имеет место неравенство 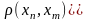. Положим m=N+1 (оно больше, чем N). Тогда для всех n>N имеем .

Рассмотрим множество чисел 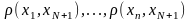. Это – конечное множество и в нем имеется наибольший элемент, который обозначим r. Тогда для любого n имеем .

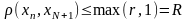Таким образом, все x_n принадлежат шару с центром в точке x_N+1 и радиусом R.

Основное определение. Метрическое пространство М называется полным, если в нем всякая фундаментальная последовательность имеет предел.

Вопрос 16.Примеры полных метрических пространств.

1. Числовая прямая .Её полнота известна из первого семестра

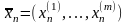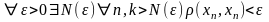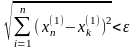2. Пространствоⁿ. Его полнота следует из того, что если и - фундаментальная последовательность, т.е. , то это означает, что , откуда 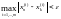и, следовательно, для каждого 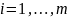последовательность 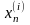- фундаментальная.

Ввиду полноты  это означает, что .

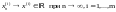Следовательно, .

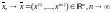3. Пространство 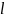² - полное. Напомним, что гильбертово пространство l² состоит из бесконечных последовательностей 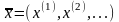, , 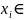i=1,2,…, обладающих свойством 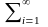x⁽ⁱ⁾² < ∞

Расстояние в нём задано, как

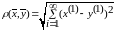
Фундаментальность последовательности означает, что

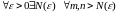
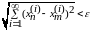
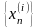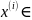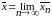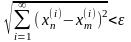откуда, как и выше, получаем, что для каждого i,i=1,2,… последовательность - фундаментальная, поэтому для каждого i=1,2,… существует предел . Осталось доказать, что Для этого рассмотрим неравенство /2

Из него для любого 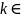получим 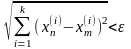/2.

В этом неравенстве перейдём к пределу при k _.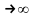

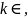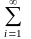
Так как оно верно для любого ряд 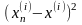cходится и выполняется неравенство

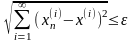/2, что и означает, что 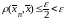. Таким образом, 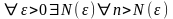, что означает что .

4. Полнота пространства непрерывных на отрезке функций с метрикой, определяющей равномерную сходимость, следует из теоремы о том, что последовательность непрерывных функций, сходящаяся равномерно, имеет пределом непрерывную функцию.