
- •1. Опишите свойства алгебраических и трансцендентных уравнений. 3
- •Опишите свойства алгебраических и трансцендентных уравнений.
- •2. Для чего производится процедура отделения корней и предварительное исследование уравнений. Приведите пример.
- •3. Приведите примеры известных вам способов исследования нелинейных уравнений.
- •4. Опишите основные свойства прямых и итерационных методов решения уравнений.
- •5. Что понимают под сходимостью итерационной процедуры? Ответпоясните примерами.
- •6. Что такое область сходимости применительно к итерационной процедуре?
- •7. Поясните, что такое скорость сходимости и как она связана с эффективностью метода.
- •8. Опишите метод половинного деления.
- •9. Опишите метод хорд. Назовите его достоинства и недостатки.
- •10. Опишите метод секущих. Дайте его сравнительную характеристику.
- •11. Опишите метод касательных (Ньютона). Укажите его достоинства и недостатки.
- •12. Опишите метод простой итерации. Дайте его характеристику.
- •13. Приведите пример итерационного метода, использующего квадратичную интерполяцию для решения нелинейных уравнений на эвм.
- •14. Какие специальные методы применяются для решения алгебраических уравнений?
- •15. Почему на практике часто применяют комбинированные алгоритмы, включающие в себя различные методы отыскания корней?
- •16. Расскажите об особенностях представления чисел в эвм. Каквлияет способ представления чисел в эвм на точность расчетов?
- •17. Что такое машинный нуль, машинная бесконечность имашинное ε ? Как эти параметры влияют на точность расчетов на эвм?
- •18. Для чего используется нормировка уравнений при их решении наЭвм?
- •19. Назовите три основных источника погрешностей при решении задач на эвм, их природу и способы уменьшения.
2.4. Контрольные вопросы
1. Опишите свойства алгебраических и трансцендентных уравнений.
2. Для чего производится процедура отделения корней и предваритель-
ное исследование уравнений. Приведите пример.
3. Приведите примеры известных вам способов исследования нелиней-
ных уравнений.
4. Опишите основные свойства прямых и итерационных методов реше-
ния уравнений.
5. Что понимают под сходимостью итерационной процедуры? Ответ
поясните примерами.
6. Что такое область сходимости применительно к итерационной про-
цедуре?
7. Поясните, что такое скорость сходимости и как она связана с эффек-
тивностью метода.
8. Опишите метод половинного деления.
9. Опишите метод хорд. Назовите его достоинства и недостатки.
10. Опишите метод секущих. Дайте его сравнительную характеристику.
11. Опишите метод касательных. Укажите его достоинства и недостатки.
12. Опишите метод простой итерации. Дайте его характеристику.
13. Приведите пример итерационного метода, использующего квадра-
тичную интерполяцию для решения нелинейных уравнений на ЭВМ.
14. Какие специальные методы применяются для решения алгебраиче-
ских уравнений?
15. Почему на практике часто применяют комбинированныеалгорит-
мы, включающие в себя различные методы отыскания корней?
16. Расскажите об особенностях представления чисел в ЭВМ. Как
влияет способ представления чисел в ЭВМ на точность расчетов?
17. Что такое машинный нуль, машинная бесконечность и
машинное ε ? Как эти параметры влияют на точность расчетов на ЭВМ?
18. Для чего используется нормировка уравнений при их решении на
ЭВМ?
19. Назовите три основных источника погрешностей при решении за-
дач на ЭВМ, их природу и способы уменьшения.
Оглавление
1. Опишите свойства алгебраических и трансцендентных уравнений. 3
2. Для чего производится процедура отделения корней и предварительное исследование уравнений. Приведите пример. 4
3. Приведите примеры известных вам способов исследования нелинейных уравнений. 5
4. Опишите основные свойства прямых и итерационных методов решения уравнений. 6
5. Что понимают под сходимостью итерационной процедуры? Ответпоясните примерами. 7
6. Что такое область сходимости применительно к итерационной процедуре? 7
7. Поясните, что такое скорость сходимости и как она связана с эффективностью метода. 9
8. Опишите метод половинного деления. 9
9. Опишите метод хорд. Назовите его достоинства и недостатки. 11
10. Опишите метод секущих. Дайте его сравнительную характеристику. 13
11. Опишите метод касательных (Ньютона). Укажите его достоинства и недостатки. 13
12. Опишите метод простой итерации. Дайте его характеристику. 15
13. Приведите пример итерационного метода, использующего квадратичную интерполяцию для решения нелинейных уравнений на ЭВМ. 17
14. Какие специальные методы применяются для решения алгебраических уравнений? 17
15. Почему на практике часто применяют комбинированные алгоритмы, включающие в себя различные методы отыскания корней? 18
16. Расскажите об особенностях представления чисел в ЭВМ. Каквлияет способ представления чисел в ЭВМ на точность расчетов? 18
17. Что такое машинный нуль, машинная бесконечность имашинное ε ? Как эти параметры влияют на точность расчетов на ЭВМ? 19
18. Для чего используется нормировка уравнений при их решении наЭВМ? 20
19. Назовите три основных источника погрешностей при решении задач на ЭВМ, их природу и способы уменьшения. 20
Вычислительные (численные) методы — методы решения математических задач в численном виде (см. Компьютерная алгебра)[1]
Представление как исходных данных в задаче, так и её решения — в виде числа или набора чисел
В системе подготовки инженеров технических специальностей является важной составляющей.
Основами для вычислительных методов являются:
решение систем линейных уравнений
интерполирование
численное интегрирование
численное решение системы нелинейных уравнений
численное решение обыкновенных дифференциальных уравнений
Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Опишите свойства алгебраических и трансцендентных уравнений.
К алгебраическим относят уравнения, в которых функция f(x) является
степенныммногочленом, тоесть
![]()
где
![]() – коэффициенты, а n
– целое число, соответст-
– коэффициенты, а n
– целое число, соответст-
вующее максимальной степени многочлена. Подобное уравнение было рас-
смотрено выше.
К трансцендентным относят уравнения, содержащие трансцендентные
функции, то есть показательную, логарифмическую, тригонометрические
функции.
Свойства алгебраических уравнений
Уравнение степени n имеет всего n корней, среди которых могут быть как действительные, так и комплексные.
Комплексные корни образуют комплексно-сопряженные пары, т. е. каждому корню x=c+idсоответствует корень x=c-id.
Число положительных действительных корней меньше или равно числу перемен знаков в последовательности коэффициентов a0, a1,…, an. Заменяя x на -x в уравнении (5), таким же способом можно оценить число отрицательных корней.
Одним из способов решения уравнения (5) является метод понижения порядка. Он состоит в том.что после нахождения какого-либо корня x = c данное уравнение можно разделить на x-c, понизив его порядок до n-1. Правда, при таком способе нужно помнить о точности, поскольку даже небольшая погрешность в значении первого корня может привести к накапливанию погрешности в дальнейших вычислениях.
Для уменьшения погрешностей лучше сначала находить меньшие по модулю корни многочлена и сразу удалять их из уравнения, приводя его к меньшей степени. Поэтому, если отсутствует информация о величинах корней, в качестве начальных приближений принимают числа 0, ± 1 и т. д.
Свойства алгебраических и трансцендентных уравнений существенно
различаются. Поэтому различны и подходы к их решению.
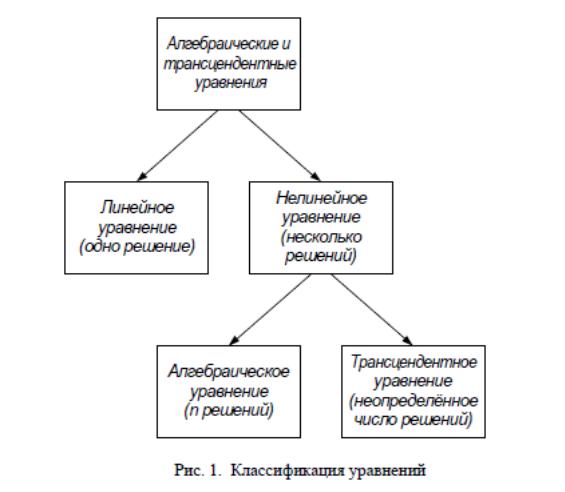 Рис.
1. Классификация уравнений
Рис.
1. Классификация уравнений
Для алгебраических уравнений до четвертого порядка включительно
известны прямые точные методы решения. Кроме того, количество корней
можно определить по степени многочлена, а их характер по знакам коэффи-
циентов этого многочлена.
Для трансцендентных уравнений общих приемов решения кроме при-
ближенных не существует. Количество корней такого уравнения обычно не-
возможно определить заранее по его виду. Трансцендентное уравнение мо-
жет не иметь ни одного вещественного корня, иметь счетное количество кор-
ней или бесконечное множество корней.
