
- •Подготовка к итоговой аттестации и решение экзаменационных задач Предисловие
- •Содержание
- •Тригонометрические выражения
- •Рекомендации
- •Примеры выполнения заданий
- •Тригонометрические уравнения
- •Простейшие тригонометрические уравнения
- •2.2. Примеры выполнения заданий
- •Пример 2 (вариант 3 №3)
- •Пример 3 (вариант 26 №3)
- •Тригонометрические уравнения, сводящиеся к квадратным.
- •Примеры выполнения заданий Пример 1 (4.13)
- •Пример 2 (4.1)
- •Пример 3 (5.1)
- •Решение тригонометрических уравнений разложением на множители
- •2.6 Однородные тригонометрические уравнения
- •Системы тригонометрических уравнений
- •2. Логарифмические выражения, уравнения, неравенства, системы
- •2.1. Логарифмические выражения
- •2.2. Логарифмические уравнения
- •Логарифмические неравенства
- •Системы логарифмических уравнений
- •3. Показательная функция.
- •Показательные уравнения
- •Показательные неравенства
- •Системы показательных уравнений
- •4. Степени
- •4.1. Упрощение выражений, содержащих степени
- •5. Иррациональные уравнения
- •5.1. Рекомендации
- •5.2. Решение уравнений, содержащих один радикал
- •6. Некоторые способы решения уравнений и неравенств
- •6.1. Алгоритм решения неравенств методом интервалов
- •6.2. Примеры выполнения заданий.
- •7.2. Физический смысл производной
- •7.3. Геометрический смысл производной
- •7.4 Касательная к графику функции
- •7.5 Наибольшее и наименьшее значения функции
- •8. Первообразная
- •8.1. Типовые задания по теме
- •8.2. Нахождение площади криволинейной трапеции
Пример 2 (4.1)
Решите уравнение

Решение

1
-
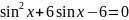 ,
,

t2 – 6t +5 = 0;
D = 36 – 20 = 16>0;

+
 +
+
Пример 3 (5.1)
Решите
уравнение -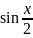 =
=
 .
.
Решение
- = ,

 +
+

1
–

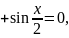
 .
.
Обозначим

2t2 –t – 1 = 0; D = 1 + 8 = 9,
t1
=
= - ,
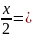 (-1)n+1
+
,
(-1)n+1
+
,
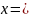 (-1)n+1
(-1)n+1
 +
+
 .
.
 ,
,
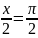 +
+


(-1)n+1
+

 ,
,
Решение тригонометрических уравнений разложением на множители
Данное выражение представляется в виде произведения нескольких сомножителей. В случае, когда выражение равно нулю, каждый из них приравнивается к нулю и уравнение сводится к более простому.
Пример 1 (4.27)
Решите уравнение
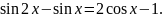
Решение
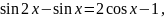
 ,
,


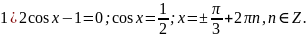
2) +
+
Ответ:
 +
+

Пример 2 (6.23)
Решите уравнение
1
+ sin
3x
=

Решение
1
+
sin
3x
=

1
+ sin
3x
=
cos2 sin2
sin2
1 + sin3x = 1 – sinx,
sin 3x + sin x = 0,
2sin 2x cos x = 0,
sin2x
= 0, 2x

cos
x = 0, x =
 +
+

Ответ:
 +
+

2.6 Однородные тригонометрические уравнения
Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным.
Его можно решать, выполнив деление на старшую степень косинуса (или синуса).
Пример 1( 4.35)
Найдите
все решения уравнения
 принадлежащих отрезку [-2
принадлежащих отрезку [-2
Решение
делим уравнение почленно на cosx ( заметим: если в данное уравнение подставить cosx =0, то получим sinx = 0, что невозможно, значит, в результате деления на cosx не будет потери корней) и находим:
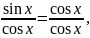
tg
x
= 1, x
=
 +
+


n
= 0, x
=
 [-2
[-2
n
= 1, x
=
 [-2
[-2
n
= -1, x
=

 [-2
[-2
n
= -2, x
=
 [-2
[-2
Ответ:
Пример 2( 5.13)
Решите уравнение
6sin2 x + sin x cos x – cos2 x = 0.
Решение
6sin2
x
+ sin
x
cos
x
–
cos2
x
= 0, так как cos
2 x
 0.
То делим почленно на cos2
x
0.
То делим почленно на cos2
x
6tg 2 x + tg x – 1 = 0.
Пусть tg x = t, тогда
6t 2 + t – 1 = 0; D = 1 + 24 = 25;
 =
=
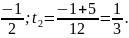
tg x =

tg x =
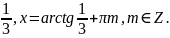
Ответ:
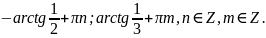
Системы тригонометрических уравнений
Решение систем тригонометрических уравнений чаще всего сводится к решению алгебраических систем относительно sin x, cos x, tg x и т.п.
Необходимо отметить, что при решении простейших уравнений нужно писать различные целочисленные параметры n и k. Если бы мы использовали одну и ту же букву, было бы потеряно бесконечное множество решений.
Есть и иной способ решения систем, в котором может использоваться способ выражения одного переменного через другое и подстановка во второе уравнение.
Решение системы записывается в виде упорядоченных пар (x; y).
Примеры выполнения заданий
Пример 1 (5.15)
Решите систему уравнений

Решение


4y + 10 – 2y = 19,
2y = 9,
y = 4,5;


x = (-1)n + ;
Ответ:
( (-1)n
+
 .
.
2. Логарифмические выражения, уравнения, неравенства, системы
Справочный материал
Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести a, чтобы получить b, причем a >0, a ≠ 1, b > 0.
 =
c
,
(1)
=
c
,
(1)

Основное логарифмическое тождество
 (2)
(2)
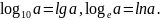
Логарифмическая функция
y=

Свойства
D (y) = R+.
E(y) = R.
При a > 1 функция монотонно возрастает на R+ и при 0 <a <1 функция монотонно убывает на R+.
При x= 1 значение функции y = 0.
