
- •1. Основні поняття та визначення елементів теорії множин.
- •2.Співвідношення між множинами. Операції над множинами
- •3. Відображення
- •4. Структурні елементи та фізичні величини електричного кола
- •5.Основні рівняння електричного кола аналіз електричного кола на базі його основних рівнянь. А також вузлових і контурних рівнянь
- •6. Метод незалежних струмів. Метод контурних струмів
- •7. Метод незалежних напруг. Метод вузлових напруг. Метод міжвузлових напруг. Метод координат віток
- •8. Метод визначальних координат
- •9. Матриці вхідних і взаємних адмітансів, коефіцієнтів розподілу, матриці вузлових і умовних вузлових імпедансів.
- •10. Перетворення рівнянь з комплексної площини в дійсну
- •11.Основні рівняння багатополюсників.
- •12. Перетворення рівнянь багатополюсників.
- •13. Розрахунок електричних кіл з багатополюсниками. Метод підсхем
- •Основні рівняння прохідних чотириполюсників
- •15.Перетворення схем, складених з прохідних чотириполюсників
- •16. Обчислення функцій. Похибки
- •17. Інтерполяція функцій
- •18. Апроксимація функцій
- •19.Наближене диференціювання функцій
- •20. Наближене інтегрування функцій
- •21. Розв’язування алгебричних і трансцендентних координатних рівнянь однієї змінної чисельними методами
- •22. Аналітичні методи розв’язування систем лінійних рівнянь
- •23. Оптимізація аналітичних методів розв'язування систем скінченних рівнянь.
- •24. Методи упаковування розріджених матриць і векторів.
- •25.Власні значення та власні вектори матриць. Зумовленість матриці. Метод qr. Норми матриці та вектора
- •26.Чисельні методи розв’язування систем лінійних скінченних рівнянь
- •29. Математичні моделі аналізу усталених ежимів еес у методі контурних струмів
- •30. Аналіз усталених режимів еес методом балансу потужностей
- •31. Лінійні диференційні рівняння з постійними коефіцієнтами.
- •32. Однокрокові явні методи.
- •33.Однокрокові неявні методи
- •34. Багатокрокові явні методи.
- •35. Ітераційний метод визначення усталеного режиму електричного кола.
- •36. Лінеаризація нелінійних диференційних рівнянь. Розв’язування крайової задачі.
- •39. Заміна аргумента диференціальних рівнянь
- •40. Методи декомпозиції
- •41. Узагальнений аналітичний метод розв’язування лінійних диференційно-скінченних рівнянь
- •42. Основи теорії стійкості режимів енергетичних систем
- •43. Алгебричні критерії стійкості. Частотні критерії стійкості.
- •44. Виділення областей стійкості. Спосіб d-розбиття. Аналіз динамічної стійкості режиму енергетичних систем.
- •45. Основні теореми ймовірностей, формули повної ймовірності, Бейєса (теорема гіпотез) і повторення дослідів
- •46. Випадкові величини в електроенергетиці
- •49. Визначення статистичних законів розподілу випадкових величин. Визначення статистичних числових характеристик випадкових величин.
- •50. Вирівнювання статистичних законів розподілу. Перевірка правильності гіпотез. Точкові оцінки. Довірчий інтервал. Довірча ймовірність
- •51. Основні положення теорії випадкових функцій.
- •52. Поняття про стаціонарний випадковий процес. Елементи теорії інформації
- •53. Метод монте-карло в задачах електроенергетики
- •54. Математичні основи теорії надійності
- •57. Деякі задачі лінійного програмування eec
- •58. Лінеаризація задачі опуклого програмування. Теорема Куна-Танкера. Умови Куна-Таккера
- •59.Чисельні методи розв'язування задач нелінійного програмування.
- •60. Динамічне програмування.
43. Алгебричні критерії стійкості. Частотні критерії стійкості.
АЛГЕБРИЧНІ КРИТЕРІЇ СТІЙКОСТІ
Такі критерії стійкості справедливі для випадку алгебричних характеристичних рівнянь
|
і є групою нерівностей, складених з коефіцієнтів цих рівнянь, при задовільненні яких рівняння відповідають стійкій системі у першому наближенні.
Необхідною умовою асимптотичної стійкості рівноваги системи, як це показано далі, є наявність усіх додатних дійсних коефіцієнтів рівняння (1). Це означає, що для нестійкості системи досить наявності в характеристичному рівнянні одного від'ємного коефіцієнта.
Необхідної умови не досить для збереження стійкості, потрібно, щоб задовольнялися ще й достатні умови. Серед алгебричних критеріїв стійкості ці вимоги формулює критерій Гурвіца або критерій Рауса.
Критерій
Гурвіца
складається за таким алгоритмом. З
коефіцієнтів рівняння (1) формують
квадратну
-го
порядку матрицю Гурвіца. за схемою (при
![]() )
)
1
2 3 4 …
![]()
|
в якій усі коефіцієнти з індексом, більшим від, замінені нулями. Критерій Гурвіца складається з п нерівностей, одержаних з матриці за правилом головних мінорів.
Необхідною умовою стійкості стану рівноваги є наявність усіх додатних коефіцієнтів характеристичного рівняння.
Критерій
Рауса
звичайно ефективний при високих порядках
характеристичних рівнянь. В основу
визначення цього критерію покладено
таблицю
Рауса,
складену з коефіцієнтів характеристичного
рівняння (1) за наступним алгоритмом. У
два перші зі загальної кількості
![]() рядків таблиці Рауса заносять відповідно
парні та непарні коефіцієнти. Елементи
наступних рядків записують за формулами
рядків таблиці Рауса заносять відповідно
парні та непарні коефіцієнти. Елементи
наступних рядків записують за формулами
|
де
—
номер рядка;
![]() — номер стовпця. В елементах нульового
стовпця таблиці записують коефіцієнти.
— номер стовпця. В елементах нульового
стовпця таблиці записують коефіцієнти.
Необхідні та достатні умови стійкості стану рівноваги за Раусом (критерій Рауса) подають у формі нерівностей
|
У випадку коренів характеристичного рівняння на межі стійкості наведена форма алгоритму Рауса неефективна й вимагає певного перетворення.
ЧАСТОТНІ КРИТЕРІЇ СТІЙКОСТІ
Ці критерії грунтуються на побудові частотних характеристик характеристичних рівнянь.
Частотною
характеристикою функції
![]() називається залежність, виражена цією
функцією, коли замість у загальному
випадку комплексного параметра
підставити
уявний параметр
називається залежність, виражена цією
функцією, коли замість у загальному
випадку комплексного параметра
підставити
уявний параметр
![]() який може змінюватися у межах
який може змінюватися у межах
![]() Наприклад, для характеристичного
рівняння (1) частотна характеристика
виражається
Наприклад, для характеристичного
рівняння (1) частотна характеристика
виражається
|
Годограф
![]() ,
побудований у комплексній площині,
називають амплітудно-фазовою
характеристикою функції;
залежність
,
побудований у комплексній площині,
називають амплітудно-фазовою
характеристикою функції;
залежність
![]() –
амплітудною
чи
амплітудно-частотною характеристикою
функції; залежність
–
амплітудною
чи
амплітудно-частотною характеристикою
функції; залежність
![]() —
фазовою
чи
фазо-частотною характеристикою функції.
Відповідно
—
фазовою
чи
фазо-частотною характеристикою функції.
Відповідно
![]() і
і
![]() —
дійсна та уявна частотні характеристики
функції.
—
дійсна та уявна частотні характеристики
функції.
Рівняння (5) запишемо
|
де
![]() корені
характеристичного рівняння (1);
корені
характеристичного рівняння (1);
![]()
Для
виведення одного з найчастіше
застосовуваних
частотних критеріїв — критерію Михайлова
знайдемо, як змінюється аргумент
комплексного множника
![]() при
зміні
при
зміні
![]() від 0 до
від 0 до
![]() у випадку дійсних від'ємних і
комплексно-спряжених з від'ємними
дійсними частинами коренів
у випадку дійсних від'ємних і
комплексно-спряжених з від'ємними
дійсними частинами коренів
![]()
Критерій Михайлова стійкості стану рівноваги записується
|
де
![]() —повна
зміна аргументу частотної характеристики
(3) при зміні
від 0 до
—повна
зміна аргументу частотної характеристики
(3) при зміні
від 0 до
![]()
На практиці критерій Михайлова застосовують на основі графічної побудови чи табличного обчислення годографа, з якого визначають аргумент . Стійкість оцінюють шляхом порівняння аргументу з (7).

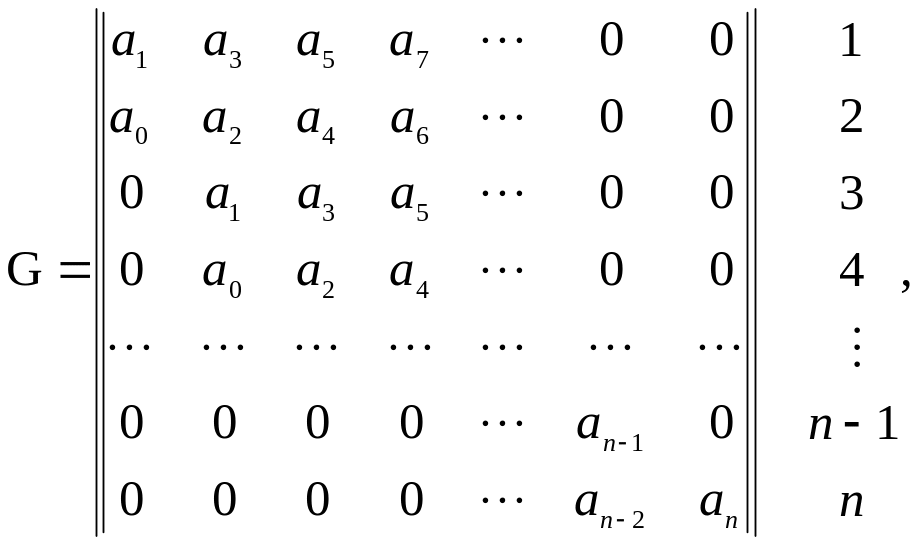 (2)
(2)