
- •1. Основні поняття та визначення елементів теорії множин.
- •2.Співвідношення між множинами. Операції над множинами
- •3. Відображення
- •4. Структурні елементи та фізичні величини електричного кола
- •5.Основні рівняння електричного кола аналіз електричного кола на базі його основних рівнянь. А також вузлових і контурних рівнянь
- •6. Метод незалежних струмів. Метод контурних струмів
- •7. Метод незалежних напруг. Метод вузлових напруг. Метод міжвузлових напруг. Метод координат віток
- •8. Метод визначальних координат
- •9. Матриці вхідних і взаємних адмітансів, коефіцієнтів розподілу, матриці вузлових і умовних вузлових імпедансів.
- •10. Перетворення рівнянь з комплексної площини в дійсну
- •11.Основні рівняння багатополюсників.
- •12. Перетворення рівнянь багатополюсників.
- •13. Розрахунок електричних кіл з багатополюсниками. Метод підсхем
- •Основні рівняння прохідних чотириполюсників
- •15.Перетворення схем, складених з прохідних чотириполюсників
- •16. Обчислення функцій. Похибки
- •17. Інтерполяція функцій
- •18. Апроксимація функцій
- •19.Наближене диференціювання функцій
- •20. Наближене інтегрування функцій
- •21. Розв’язування алгебричних і трансцендентних координатних рівнянь однієї змінної чисельними методами
- •22. Аналітичні методи розв’язування систем лінійних рівнянь
- •23. Оптимізація аналітичних методів розв'язування систем скінченних рівнянь.
- •24. Методи упаковування розріджених матриць і векторів.
- •25.Власні значення та власні вектори матриць. Зумовленість матриці. Метод qr. Норми матриці та вектора
- •26.Чисельні методи розв’язування систем лінійних скінченних рівнянь
- •29. Математичні моделі аналізу усталених ежимів еес у методі контурних струмів
- •30. Аналіз усталених режимів еес методом балансу потужностей
- •31. Лінійні диференційні рівняння з постійними коефіцієнтами.
- •32. Однокрокові явні методи.
- •33.Однокрокові неявні методи
- •34. Багатокрокові явні методи.
- •35. Ітераційний метод визначення усталеного режиму електричного кола.
- •36. Лінеаризація нелінійних диференційних рівнянь. Розв’язування крайової задачі.
- •39. Заміна аргумента диференціальних рівнянь
- •40. Методи декомпозиції
- •41. Узагальнений аналітичний метод розв’язування лінійних диференційно-скінченних рівнянь
- •42. Основи теорії стійкості режимів енергетичних систем
- •43. Алгебричні критерії стійкості. Частотні критерії стійкості.
- •44. Виділення областей стійкості. Спосіб d-розбиття. Аналіз динамічної стійкості режиму енергетичних систем.
- •45. Основні теореми ймовірностей, формули повної ймовірності, Бейєса (теорема гіпотез) і повторення дослідів
- •46. Випадкові величини в електроенергетиці
- •49. Визначення статистичних законів розподілу випадкових величин. Визначення статистичних числових характеристик випадкових величин.
- •50. Вирівнювання статистичних законів розподілу. Перевірка правильності гіпотез. Точкові оцінки. Довірчий інтервал. Довірча ймовірність
- •51. Основні положення теорії випадкових функцій.
- •52. Поняття про стаціонарний випадковий процес. Елементи теорії інформації
- •53. Метод монте-карло в задачах електроенергетики
- •54. Математичні основи теорії надійності
- •57. Деякі задачі лінійного програмування eec
- •58. Лінеаризація задачі опуклого програмування. Теорема Куна-Танкера. Умови Куна-Таккера
- •59.Чисельні методи розв'язування задач нелінійного програмування.
- •60. Динамічне програмування.
22. Аналітичні методи розв’язування систем лінійних рівнянь
У випадку лінійної системи рівнянь вектор-функція (4.104) набирає вигляду
|
або
|
чи в розгорненій формі
|
Якщо
матриця
![]() неособлива, тобто
неособлива, тобто
![]() то рівняння (4.134) має єдине розв’язання,
а саме:
то рівняння (4.134) має єдине розв’язання,
а саме:
|
де обернена матриця
|
У (4.137) матриця
|
в
якій
![]() -
алгебричні доповнення елементів
-
алгебричні доповнення елементів
![]() транспонованої матриці коефіцієнтів
рівняння (4.135).
транспонованої матриці коефіцієнтів
рівняння (4.135).
При
високих порядках рівняння (4.134) пряме
знаходження оберненої матриці
![]() вимагає виконання великого обсягу
обчислень з необхідністю визначення у
загальному випадку
вимагає виконання великого обсягу
обчислень з необхідністю визначення у
загальному випадку
![]() алгебричних
доповнень.
алгебричних
доповнень.
Шляхом простих перетворень (4.136) одержуємо розв’язання (4.135) у вигляді відомого алгоритму Крамера, згідно з яким вектор-стовпець невідомих
|
де
|
що
одержується з матриці коефіцієнтів
шляхом заміни її
![]() го
стовпця вектором-стовпцем вільних
членів
го
стовпця вектором-стовпцем вільних
членів
![]()
У
формулі (4.139) здійснюється
![]() разове розкриття детермінанта вигляду
(4.140) матриці
-
го порядку, тоді як у (4.137)
разів розкриваються детермінанти
матриці
разове розкриття детермінанта вигляду
(4.140) матриці
-
го порядку, тоді як у (4.137)
разів розкриваються детермінанти
матриці
![]() -
го порядку. Оскільки під час розкриття
детермінанта
го
порядку виконується стільки ж операцій,
що й під час розкриття
детермінантів
-
го порядку. Оскільки під час розкриття
детермінанта
го
порядку виконується стільки ж операцій,
що й під час розкриття
детермінантів
![]() го
порядку, то з погляду обсягу обчислень
формули (4.137) і (4.139) рівноцінні й дуже
трудомісткі. На практиці широко
застосовують прямі методи розв’язування
рівняння (4.135) – метод
Гаусса,
метод
квадратичних коренів,
метод
Халецького
й інші.
го
порядку, то з погляду обсягу обчислень
формули (4.137) і (4.139) рівноцінні й дуже
трудомісткі. На практиці широко
застосовують прямі методи розв’язування
рівняння (4.135) – метод
Гаусса,
метод
квадратичних коренів,
метод
Халецького
й інші.
Скінченні рівняння в задачах електроенергетики, як це було показано у третьому розіділі, звичайно характеризуються високою розрідженістю матриць коефіцієнтів. Кількість ненуьових елементів (НЕ) у них дуже мала. Коефіцієнт заповненя
|
де
- кількість НЕ;
![]() - вимірність матриці, для вказаних
матриць особливо при їхніх високих
вимірностях дуже низький. Наприклад,
для матриці вузлових адмітансів
- вимірність матриці, для вказаних
матриць особливо при їхніх високих
вимірностях дуже низький. Наприклад,
для матриці вузлових адмітансів
![]() де кількість НЕ можна визначити за
формулою
де кількість НЕ можна визначити за
формулою
![]() в якій
в якій![]() -
середня кількість НЕ в рядку матриці.
Отже,
-
середня кількість НЕ в рядку матриці.
Отже,
![]() Максимальне значення
відповідає повній планарній схемі
електро-енергетичної мережі і становить
=5
(один НЕ, що відповідає власному
адмітансові вузла, та чотири НЕ – взаємні
адмітанси). Отже, при
Максимальне значення
відповідає повній планарній схемі
електро-енергетичної мережі і становить
=5
(один НЕ, що відповідає власному
адмітансові вузла, та чотири НЕ – взаємні
адмітанси). Отже, при
![]() вузлів
вузлів
![]() ,
а при
,
а при
![]() вузлах
вузлах
![]()
23. Оптимізація аналітичних методів розв'язування систем скінченних рівнянь.
Серед
аналітичних методів розв'язування
систем скінченних рівнянь найефективніший
метод послідовних виключень -
метод Гаусса з триангуляцією та подвійною
факторизацією матриць. З цього погляду
вирішальне значення має вибір порядку
(впорядкування) виключення невідомих,
мета якого -
забезпечення високої точності обчислень,
збереження високої розрідженості
матриці та виконання якомога меншої
кількості арифметичних і логічних
операцій. Правила вибору порядку
виключення невідомих, які забезпечують
появу мінімальної кількості ННЕ,
називають
критеріями оптимальної нумерації.
Одним з найефективніших є
критерій Марковіца,
згідно з яким для чергового виключення
вибирається та невідома, індекси
коефіцієнта матриці
якої
та
![]() задовольняють умову
задовольняють умову
![]() де
де![]() -
нова кількість HHE,
що можуть
появитися під час виключення невідомої
з індексам
,
;
-
нова кількість HHE,
що можуть
появитися під час виключення невідомої
з індексам
,
;
![]() ,
-
кількість НЕ в рядку
та стовпці
матриці
відповідно (без врахування
,
-
кількість НЕ в рядку
та стовпці
матриці
відповідно (без врахування
![]() -го
елемента).
-го
елемента).
На практиці застосовують дві групи методів квазіоптимального впорядкування послідовності виключення - методи попереднього впорядкування, в яких послідовність виключення встановлюється заздалегідь, і методи динамічного впорядкування, де вона визначається в процесі виключення.
До методів попереднього впорядкування відносяться метод мінімізації кількості НЕ рядка і стовпця, що відповідають головному елементові, та метод обрамування діагоналі.
Він базується безпосередньо на критерію Марковіца. Практична його реалізація зводиться до впорядкування рівнянь системи, щоб забезпечити у першу чергу виключення тих невідомих, які зв'язані з найменшою кількістю інших невідомих. Метод обрамування діагоналі полягає в згрупуванні елементів матриці у вигляді вузької смуги-стрічки вздовж головної чи побічної діагоналі матриці. Матриці з таким згрупуванням елементів часто називають стрічковими. Вони відповідають графам такої ж структури.
Динамічне впорядкування полягає в оптимізації порядку виключення невідомих у процесі розв'язування рівняння. Такий підхід найефективніший, оскільки тут на кожному кроці обчислень можна вибрати наступний елемент виключення за критерієм оптимальності.
Серед таких методів у задачах електроенергетики застосовують метод динамічної мінімізації НЕ у рядках і стовпцях матриці та метод динамічної мінімізації ННЕ.
Метод динамічної мінімізації НЕ в рядках і стовпцях матриці формально збігається з відповідним методом попереднього впорядкування з тою різницею, що тут визначається мінімальна кількість НЕ, зв'язаних з елементом, який виключається на кожному кроці.

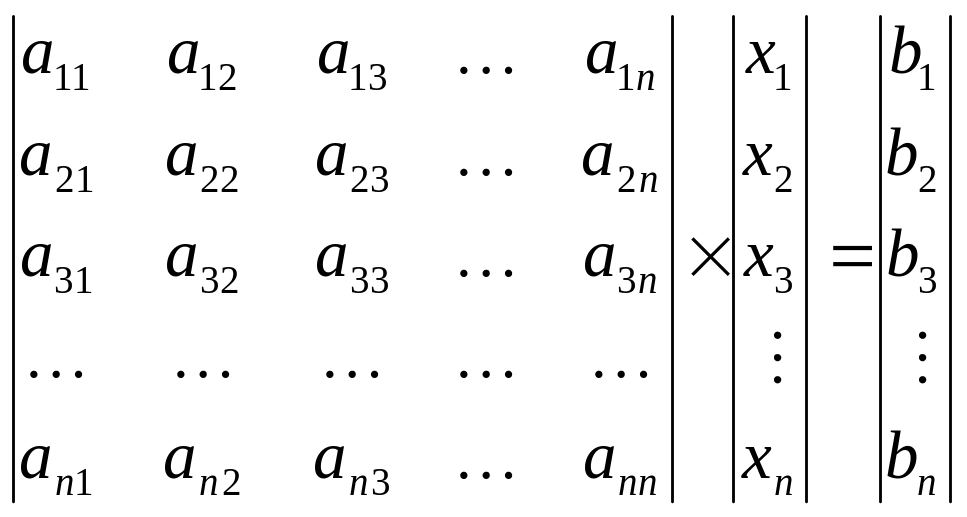 . (4.135)
. (4.135) , (4.138)
, (4.138)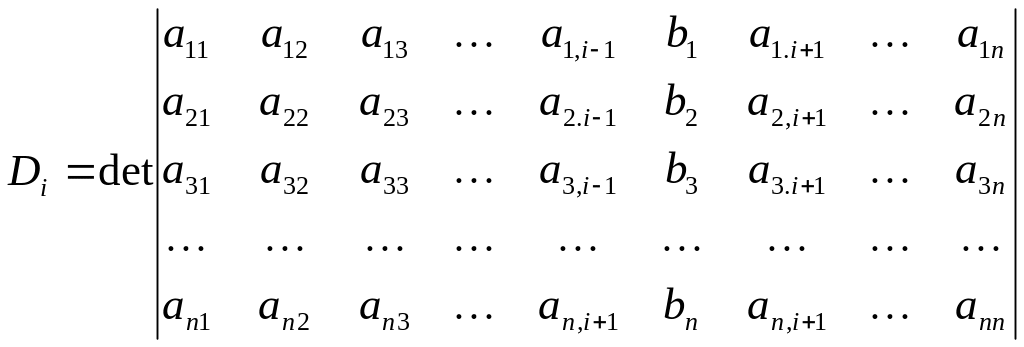 , (4.140)
, (4.140)