5.2. Определение главных моментов инерции сечения

К решению задачи рекомендуется приступить после выполне­ния самостоятельной работы 5 (гл. 1). Порядок решения задачи остается таким же.

Пример 29. Определить моменты инерции сечения, составлен­ного из прокатных профилей, относительно главных централь­ных осей (рис. 44). Сечение состоит из двутавра № 33, швеллера № 27, двух уголков 90 х 56 х 6 и листа сечением 12 х 180 мм.

Решение. 1. Положение центра тяжести определено в приме­ре 25: у_с = 2,33 см, если ось проходит через центр тяжести дву­тавра.

2. Проводим центральные оси для каждого профиля проката х_{1 ъ}

x ₂ , x₃, x₄ и х₅.

3. Проводим главные центральные оси. Вертикальную ось v со­вмещаем с осью симметрии, а горизонтальную и проводим через центр тяжести сечения С перпендикулярно оси v.

4. Определим момент инерции сечения относительно оси «:

Учитывая, что уголки одинаковые и расположены на одинако­вом расстоянии от оси и, получим:

Определим величину каждого слагаемого. Момент инерции швеллера № 27 относительно оси и

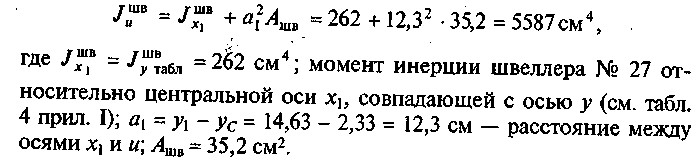
Момент инерции уголка 90 х 56 х 6 относительно оси «

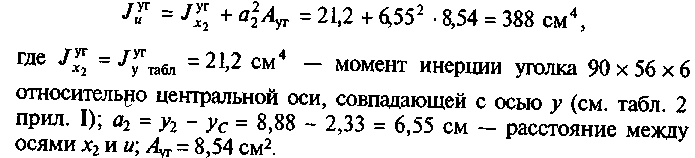
Момент инерции двутавра № 33 относительно оси и:

140

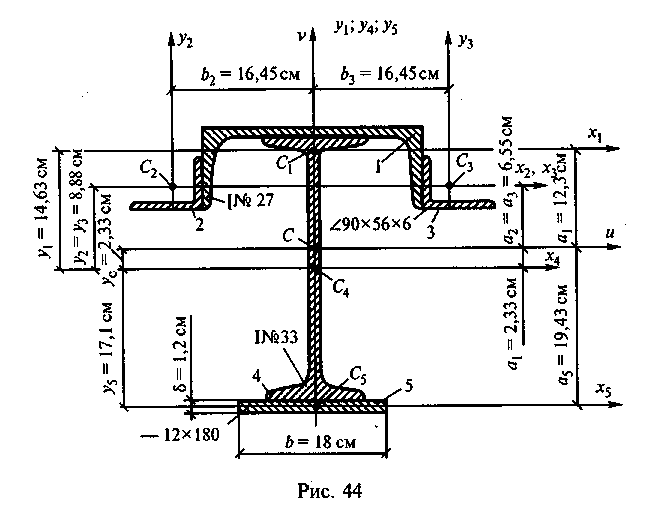
Момент инерции листа 12x180 мм относительно оси и:

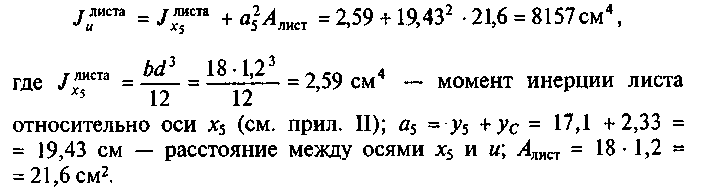
Подставим полученное значение в формулу (а):

5. Определим момент инерции сечения относительно оси v:

Момент инерции швеллера № 27 относительно оси v:

141

Момент инерции уголка 90 х 56 х 6 относительно оси v:

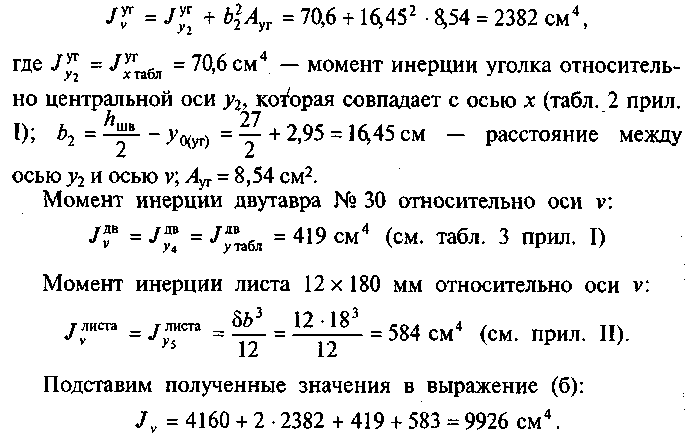
Ответ: J_u = 24652 см⁴; J_v = 9926 см⁴.

Пример 30. Определить моменты инерции сечения, состав­ленного из простых геометрических фигур, относительно глав­ных центральных осей по условию примера 25 (см. рис. 37).

Решение. 1. Положение центра тяжести определено: у_с = = 9,84 см.

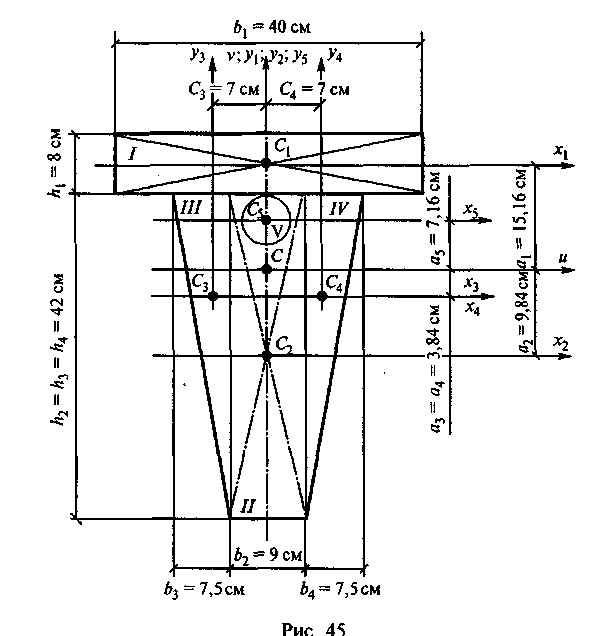
2. Для каждой фигуры проводим центральные оси х_{, х₂, х₃, х₄ и х₅, причем оси х₃ и x₄ совпали (рис. 45).

3. Проводим главные центральные оси. Вертикальную ось v со­вместим с осью симметрии, а горизонтальную ось и проведем че­рез центр тяжести сечения С перпендикулярно оси v.

4. Момент инерции сечения относительно оси и

Определим значение каждого слагаемого. Момент инерции;' первого прямоугольника

Момент инерции второго прямоугольника

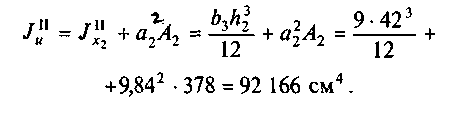
142

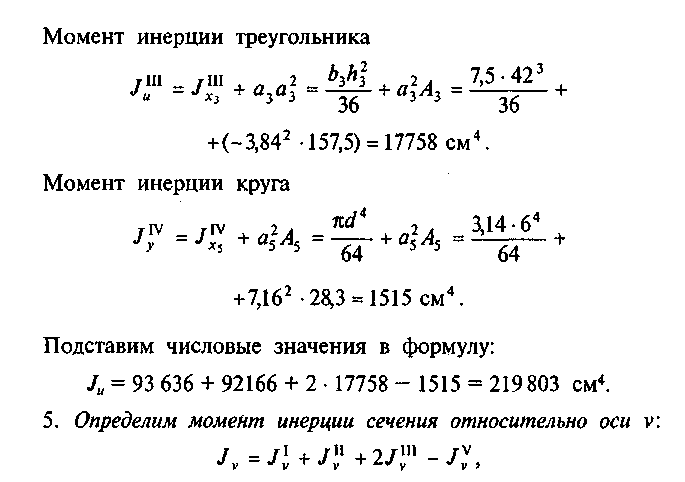
143

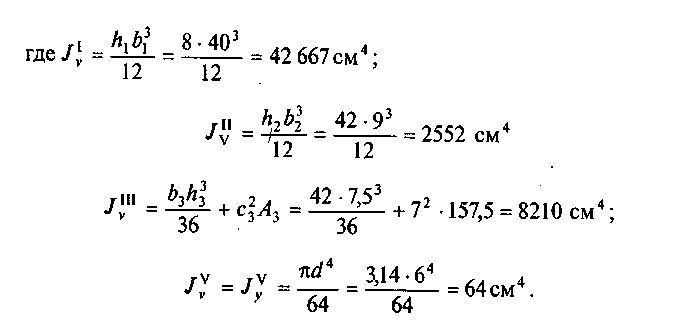
Подставим числовые значения в формулу для определения /_v:

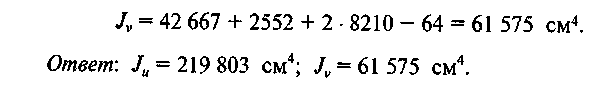
Задание для расчетно-графической работы 5.

Задача 1. Определить моменты инерции сечения, составленного из профилей прокатной стали, относительно главных центральных осей по данным одного из вариантов, приведенных на рис. 38.

Задача 2. Определить моменты инерции сечения, составленного из простых геометрических фигур, относительно главных центральных осей по данным одного из вариантов, приведенных на рис. 39.

5.3. Подбор сечения балки из прокатного двутавра

1. Строят эпюры Q_x и М_х (см. самостоятельную работу 6, гл. I).

2. Подбирают сечение стальной балки в следующем порядке: а) определяют требуемый момент сопротивления сечения балки:

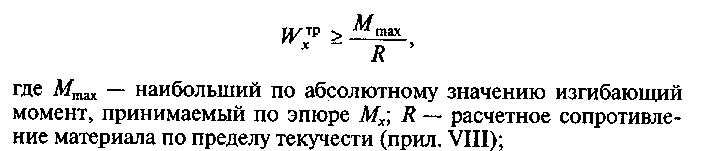
б) по ГОСТам прил. I подбираем номер двутавровой стальной балки, которая должна иметь момент сопротивления W_x, наибо­лее близкий по значению к требуемому моменту сопротивления W_x^тр

3. Проверяют прочность принятой двутавровой балки по нор­мальным напряжениям. Такую проверку выполняют для сечения с наибольшим изгибающим моментом:

144

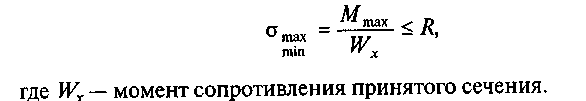
Если условие удовлетворено, прочность балки по нормальным сечениям считается обеспеченной, и наоборот.

4. Строят эпюру нормальных напряжений о. Для этого вычер­чивают крупно поперечное сечение балки и проводят на отдель­ном рисунке нулевую линию перпендикулярно нейтральной оси. Затем на уровне крайних точек сечения (верхней и нижней) от­кладывают найденные ранее значения Q_тах и Q_min и соединяют эти значения прямой линией. Полученный график называется эпюрой а. Значения Q_тах и Q_min откладывают по разные стороны от нулевой линии.

5. Проверяют прочность принятой двутавровой балки по каса­тельным, напряжениям. Наибольшие касательные напряжения возникают в том сечении по длине балки, в котором действует наибольшая поперечная сила (по абсолютному значению), а по высоте сечения — на уровне нейтрального слоя.

Для определения этих напряжений действительное сечение двутавровой балки упрощают: полка и стенка принимаются пря­моугольными: полка с размерами b и /, а стенка — d и (h — 2f). Размеры b, t и h берутся по ГОСТу (прил. I). Таким образом, се­чение двутавровой балки теперь состоит из трех прямоугольни­ков.

Касательные напряжения на уровне нейтрального слоя опре­деляют по формуле Журавского:

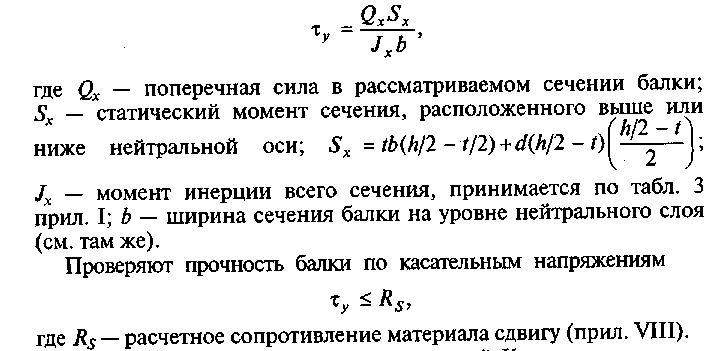
6. Строим эпюру касательных напряжении, касательные напря­жения изменяются по высоте балки по криволинейному закону и имеют скачок в месте соединения полки и стенки. Поэтому эпю­ру т строят по значениям, найденным в пяти точках сечения:

145

крайних точках, на уровне нейтральной оси и на уровне сопря­жения стенки и полки — чуть ниже и чуть выше этого сопряже­ния.

Напряжение в этих точках определяется по формуле Журав-ского. При этом статический момент S_x и ширина сечения Ь оп­ределяются для каждой точки сечения. Касательные напряжения в крайних точках сечения равны нулю.

Пример 31. По условию примера 11 подобрать сечение сталь­ной двутавровой балки (рис. 46, а). Проверить прочность приня­того сечения по нормальным напряжениям в сечении с наиболь­шим изгибающим моментом и по касательным напряжениям в сечении с наибольшей поперечной силой. Материал — сталь марки С-235.

Решение. 1. Строим эпюры Q_x и М_х (см. пример 11). Наиболь­шее значение поперечной силы Q_max = 73,6 кН, изгибающего мо­мента M_тах =95,4кН-м (см. рис. 15).

2. Подберем сечение стальной двутавровой балки по наибольше­му изгибающему моменту

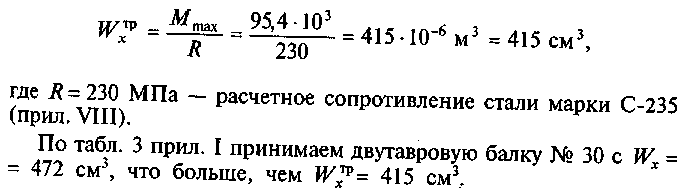
3. Проверим прочность принятого сечения:

Прочность сечения по нормальным напряжениям обеспечена.

4. Строим эпюру нормальных напряжений. Отложим от нулевой линии 0—0 (рис. 46, б) значение q_тах = 202,1 МПа и c q_min = = 202,1 МПа и соединим полученные точки. Верхняя часть испы­тывает сжатие, нижняя — растяжение, так как по эпюре М_х вид­но, что балка прогибается (обращена выпуклостью) вниз.

5. Проверим прочность балки по касательным напряжениям. За­меним действительное сечение упрощенным (рис. 46, в). Разме­ры d= 6,5 мм; t= 10,2 мм; b = 135 мм приняты по табл. 3 прил. I.

Определим наибольшее касательное напряжение

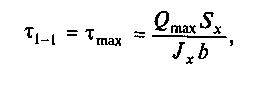
146

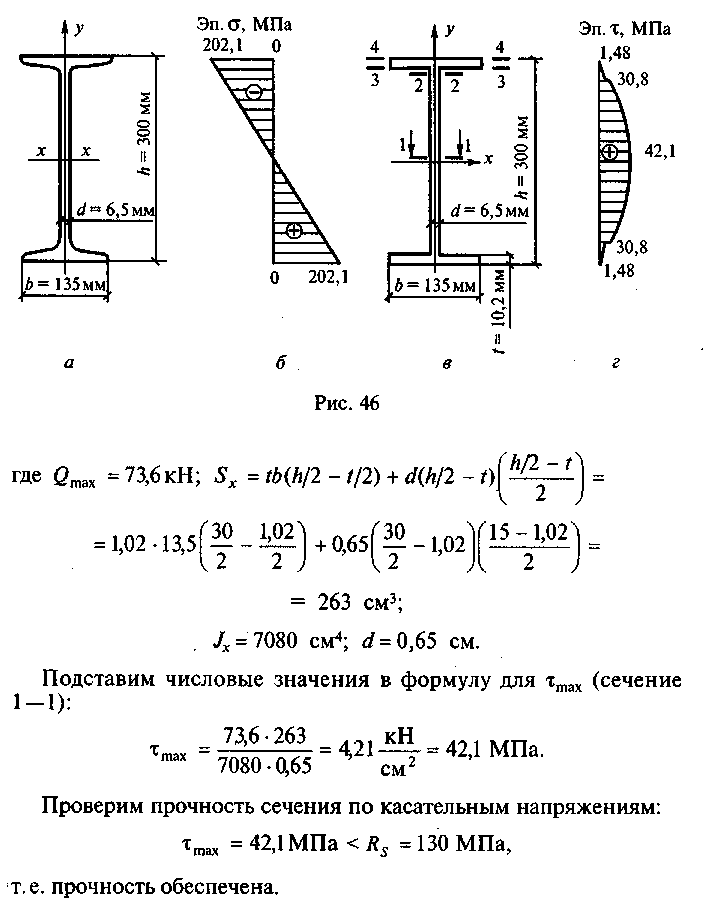
В прокатных балках, которые не несут больших сосредоточен­ных сил в приопорных участках, это условие обычно соблюдается с большим запасом.

6. Построим эпюру т. Напряжение в сечении 2 — 2

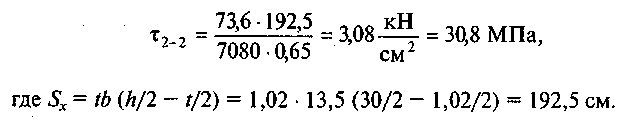
147

Напряжение в сечении 3 — 3

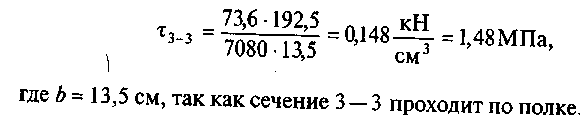
Напряжение в сечении 4 — 4 равно нулю, так как S_x = 0. По найденным значениям строим эпюру r _y (рис. 46, г).

Задание для расчетно-графической работы 6. Подобрать сечение стальной двутавровой балки, проверить принятое сечение по нормаль­ным (для сечения с наибольшим изгибающим моментом) и по касатель­ным (для сечения с наибольшей поперечной силой) напряжениям и по­строить эпюры q и r для соответствующих сечений. Материал — сталь С-245. Остальные данные принять по одному из вариантов, показанных на рис. 7.