3.4. Расчет статически неопределимой (неразрезной) балки по уравнению трех моментов

1. Обозначают пролеты и опоры на заданной схеме (системе): первый пролет — l₁ второй — /₂, третий — /₃ и т. д. Первая опораобозначается 0, вторая — 1, третья — 2 и т. д.

2. От заданной системы переходят к основной системе. Для этого каждую опору заменяют шарниром и опорным моментом, который замещает действие отброшенной связи. Опорные мо­менты обозначают М₀, М_ъ М₂, ... в зависимости от номера опо­ры. Величина этих моментов неизвестна.

Если балка имеет консоль, то в основной системе она отбра-сывается, а действие отброшенных сил приложенных к консо-ли учитывается. Если одна из крайних опор жестко защемляю-щая, то в основной системе ее заменяют шарнирной опорой и добавляют еще один пролет и опору, которые называют фиктив­ными, так как в заданной системе их нет. Длина фиктивного пролета принимается равной нулю. Если защемляющая опора расположена на левом конце, то фиктивный пролет обозначают l ₀ =0, а фиктивную опору - "-1"_. (минус первая) и опорный мо­мент M_-1 =0 защемляющая опора расположена на правом конце, то фиктивному пролету, опоре и моменту присваивается индекс, следующий за индексом предшествующего пролета (опоры, момента).

3. Определяют значения изгибающих моментов от заданной на­грузки для основной системы в каждом пролете. По найденным значениям строят эпюру моментов от заданной нагрузки для ос­новной системы, которую обозначают М _х⁰. Величины моментов и характер эпюр определяют по прил. VI.

4. Определяют неизвестные опорные моменты с помощью урав­нений трех моментов, которые составляются для каждой проме­жуточной опоры. Во всех задачах самостоятельной работы основ­ная система имеет одну промежуточную опору, в задачах расчет-но-графической работы — две. Поэтому в этих задачах составля­ются соответственно одно и два уравнения трех моментов.

Для балки, у которой в заданной системе все опоры шарнир­ные или одна (правая) защемляющая, уравнения трех моментов имеют вид:

для первой промежуточной опоры 1

для второй промежуточной опоры 2

90

где m₁ и М₂ — опорные моменты на промежуточных опорах, их определяют путем решения уравнений; М ₀ и М ₃ — опорные мо­менты на концевых опорах, их находят по схеме балки; А ₂ ^ф, А ^ф_3, B ^ф₁ , B ^ф ₂ — фиктивные опорные реакции для основной систе­мы (по прил. VII).

Если защемляющая опора расположена слева, то, учитывая все дополнительные преобразования (см. п. 2), уравнения трех моментов принимают вид:

для первой промежуточной опоры О

для второй промежуточной опоры 1

где М ₀ и М ₁ — опорные моменты на промежуточных опорах, их определяют путем решения уравнений; М _-1 и М₂ — опорные мо­менты на крайних опорах, их определяют по схеме балки; В ^ф ₀, А ^ф_1, B ^ф₁ , А ^ф ₂ — фиктивные опорные реакции для основной сис­темы (по прил. VII). В примерах они условно показаны на ос­новной системе. Подробнее о фиктивных опорных реакциях можно узнать в работе [3].

Решают уравнения и определяют опорные моменты.

5. По найденным значениям строят эпюры опорных моментов М _оп , откладывая их на соответствующих опорах с учетом полу­ченных знаков и соединяя прямыми линиями.

6. Определяют значения изгибающих моментов М_х от заданной нагрузки для заданной системы путем суммирования значения эпюр М _х⁰ и М_оп в характерных точках. По найденным значениям строят эпюру М_х. Она должна быть уточнена после построения эпюры Q_x.

7. Определяют значения поперечных сил Q_x на опорах:

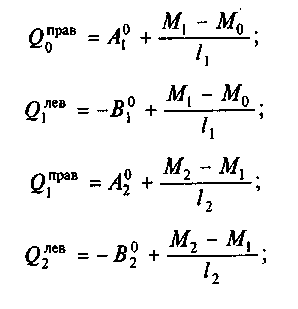
91

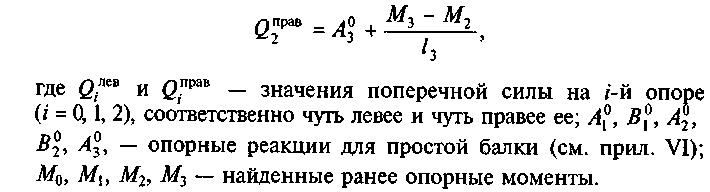
Поперечные силы на участках между опорами и на консоль­ных участках определяются по общим правилам. По найденным значениям строят эпюру Q_x, используя зависимости между на­грузкой и характером эпюры Q_x (см. самостоятельную работу 6).

8. Определяют опорные реакции балки на опорах О, 1, 2, 3:

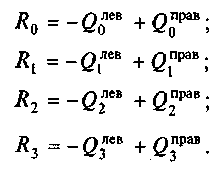
9. Уточняют эпюру М_х. Для этого находят значения изгибаю­щих моментов для тех сечений, где наклонная линия эпюры (если такая есть) пересекает нулевую линию.

В качестве проверки можно найти сумму моментов всех левых или правых сил (и опорных реакций в том числе) относительно любой точки балки. Они должны быть равны между собой.

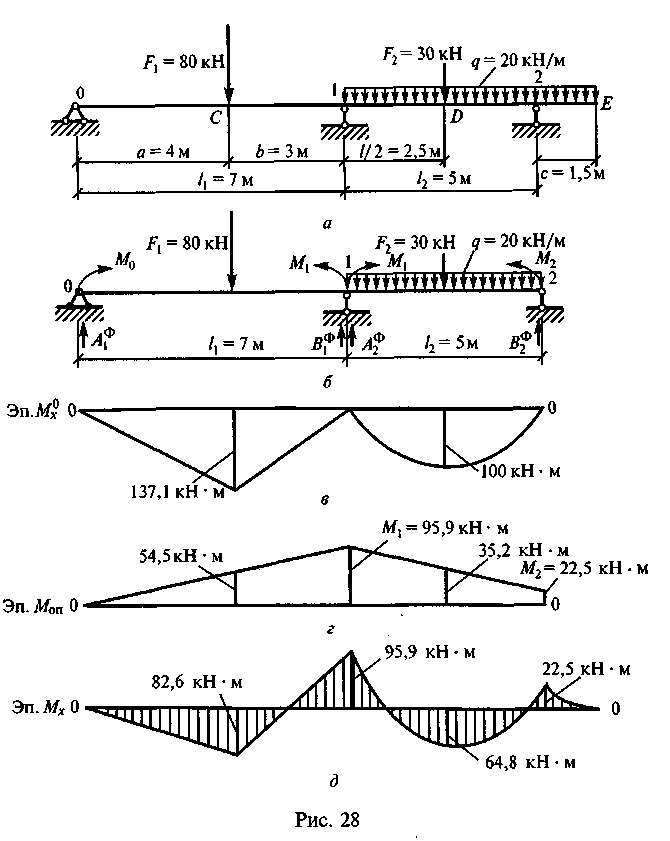
Пример 20. Построить эпюру М_х для неразрезной балки, по­казанной на рис. 28.

Решение. 1. Обозначим пролеты /, и /₂ и опоры О, 1, 2 (рис.28, а).

2. От заданной системы переходим к основной, введя на каж­дую опору шарниры и опорные моменты (рис. 28, б).

3. Определим изгибающие моменты в характерных точках для основной системы от заданной нагрузки (см. прил. VI). Момент в точке С под силой F₁ = 80 кН

момент в точке D под силой F₂ = 30 кН

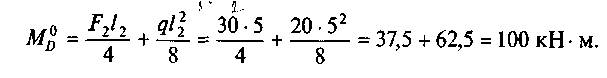
По найденным значениям строим эпюру М _х° (рис. 28, в).

92

4. Составим уравнение трех моментов. Промежуточная опора одна, поэтому и уравнение для опоры 1 будет одно:

где М₀ = 0, так как опора 0 концевая и шарнирная;

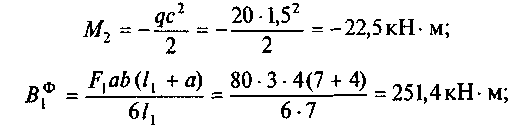
93

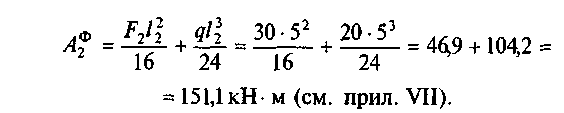
Подставим числовые значения в уравнение моментов:

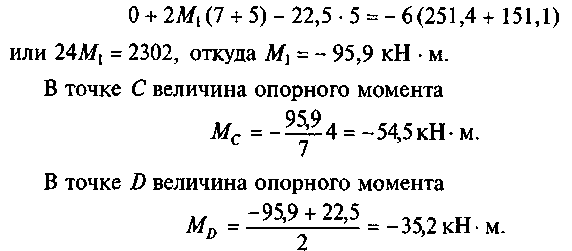
5. По найденным значениям строим эпюру М_оп>(рис. 28, г).

6. Суммируем значения эпюр М° и М_ОП в характерных точках:

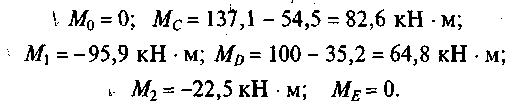
По найденным значенимя строим эпюру М_х (рис. 28, д). Пс условию самостоятельной работы требуется построить толькс эпюру М_х.

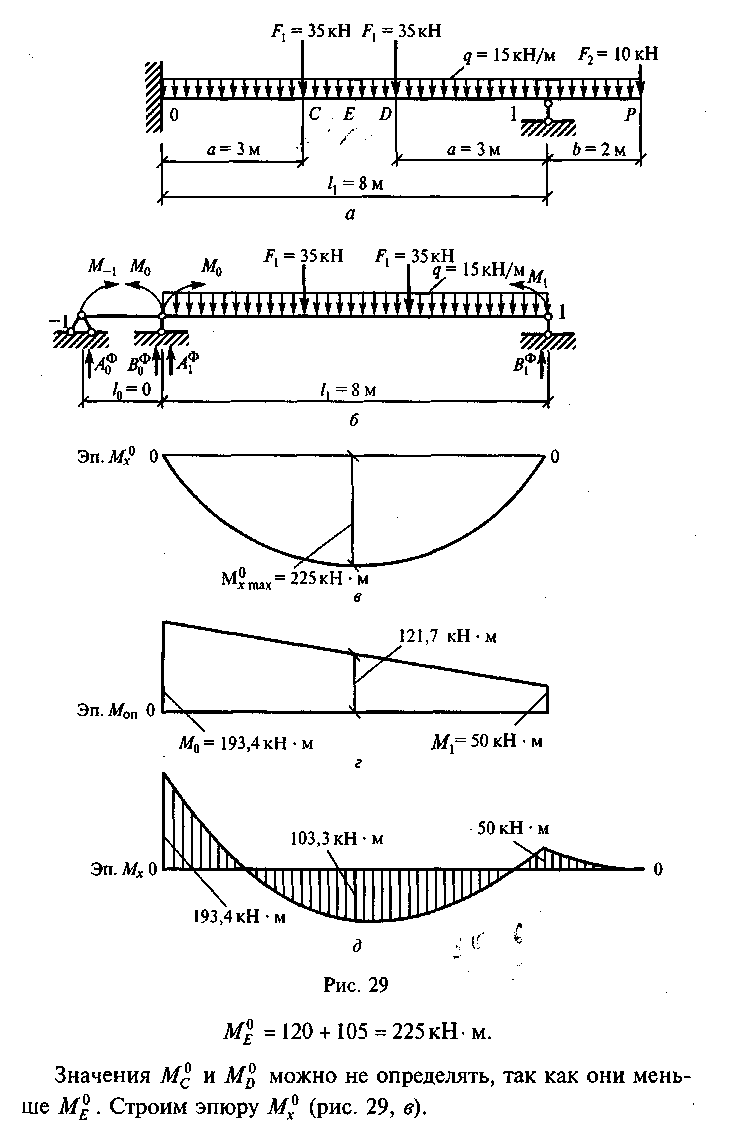
Пример 21. Построить эпюру М_х для балки, показанной на рис. 29, а.

Решение. 1. Обозначим опоры О, 1 и пролет 1₁ (рис. 29, а).

2. От заданной системы переходим к основной. Для этого вме­сто опор 0 и 1 вводим шарниры и опорные моменты М₀ и М₁ Кроме того, влево от опоры 0 вводим дополнительный (фиктив­ный) пролет /о = 0 и фиктивную опору —1с опорным моментом Af_i = 0 (рис. 29, б).

3. Определим величины изгибающих моментов в характерных точках для основной схемы от заданной нагрузки (см. прил. VI) Моменты в точках С и D от силы F_l

Момент в точке Е (середине пролета) от нагрузки q

Момент в точке Е от совместного действия силы F₁ и нагруз­ки q равен сумме моментов от каждого из них:

94

95

4. Составим уравнение трех моментов для промежуточной опоры 0:

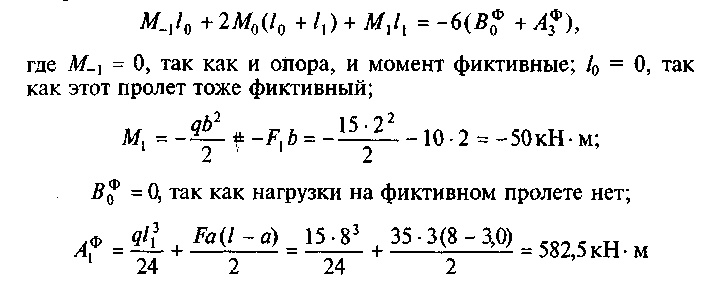
(см. прил. VII).

Подставим числовые значения в уравнение трех моментов:

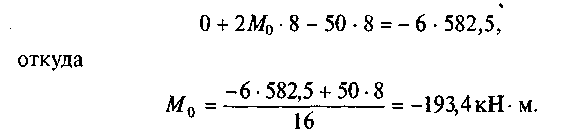
5. Строим эпюру опорных моментов М_ОП (рис. 29, г). Значение опорного момента в середине пролета (точка Е)

6. Определим значение изгибающего момента от заданной на­грузки для заданной схемы в точке Е:

Строим эпюру М_х (рис. 29, д). Она должна быть уточнена по­сле построения эпюры Q_x, но это выходит за рамки самостоятель­ной работы и будет показано в расчетно-графической работе 11.

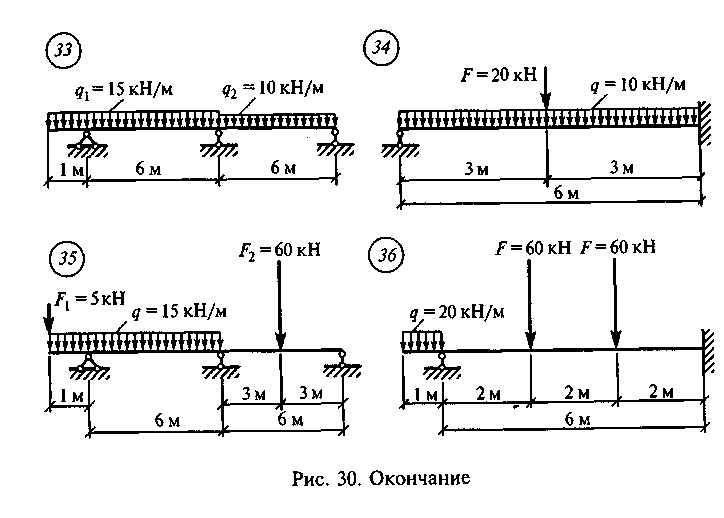
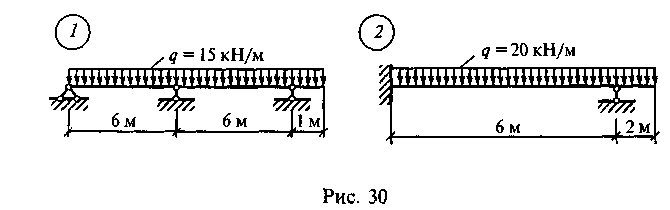
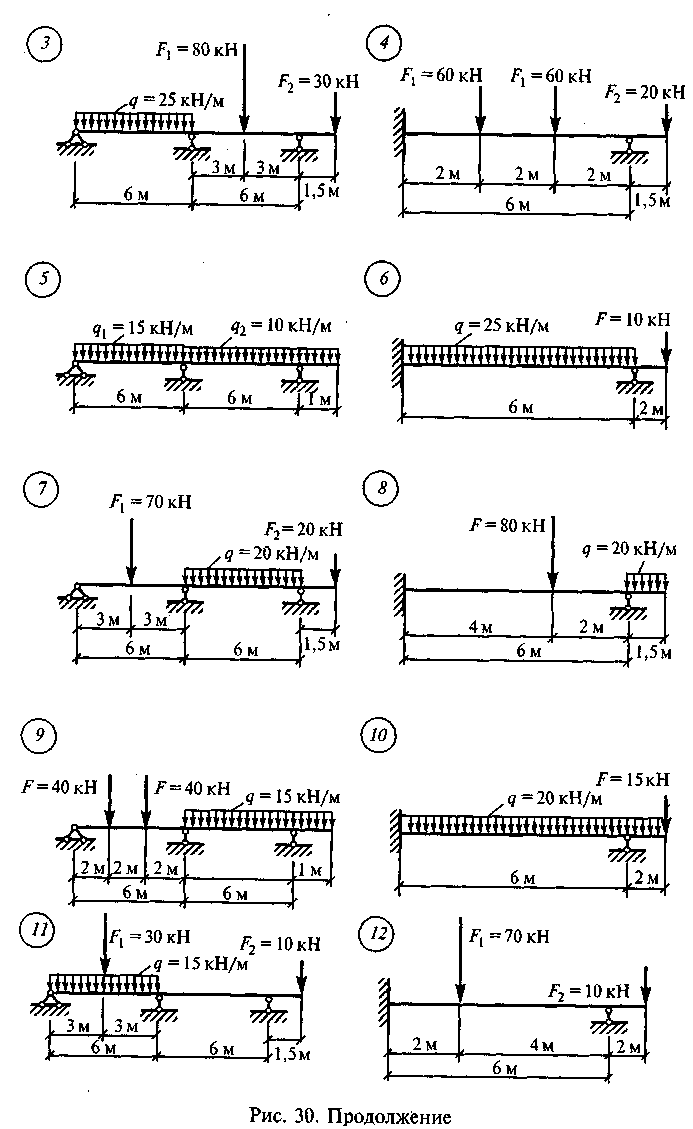
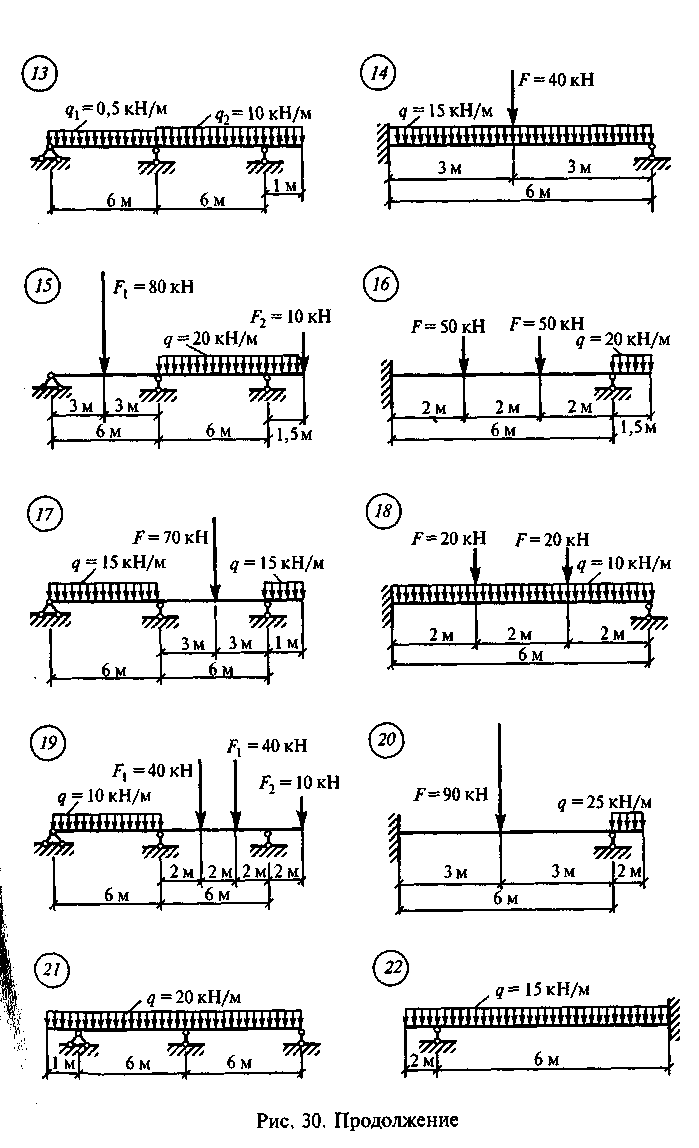
Задание для самостоятельной работы 11. Построить эпюру для нераз­резной балки по данным одного из вариантов, показанных на рис. 30.

96

97

99