- •2.1. Оптичні явища на границі розділу двох діелектричних середовищ
- •2.2. Закони Снелла
- •2.3. Повне внутрішнє відбивання
- •2.4. Закони Френеля
- •2.5. Кут Брюстера
- •2.7. Ефект Гуса-Хенхена
- •3.1. Модель зигзагоподібного поширення хвиль у тонкій плівці
- •3.2. Ефективна товщина хвилеводу
- •3.3. Моди плоского хвилеводу
- •3.4. Рівняння хвилеводних мод
- •3.5. Число мод плоского хвилеводу
- •3.6. Універсальні дисперсійні криві для плоского хвилеводу
- •4.1. Класифікація та основні типи планарних оптичних хвилеводів
- •4.2. Елементи вводу/виводу випромінювання у хвилевід
- •4.2.1. Поперечні елементи зв’язку
- •4.2.2. Поздовжні елементи зв’язку
- •4.3. Елементи зв’язку між оптичними хвилеводами
- •4.3.1. Зв’язок між плоскими планарними хвилеводами
- •4.3.2. Зв'язок між плоскими та канальними хвилеводами
- •4.3.3. Зв'язок між канальними хвилеводами
- •4.3.4. Зв'язок між планарними і волоконними хвилеводами
- •4.4. Перетворювачі мод
- •5.1. Матеріали для планарних хвилеводів
- •5.2. Процедура підготовки підкладки
- •5.3. Методи виготовлення тонкоплівкових хвилеводів
- •5.3.1. Метод розпилення
- •5.3.2. Метод плазмової полімеризації
- •5.3.3. Метод осадження з розчину
- •5.3.4. Метод дифузії
- •5.3.5. Метод іонного обміну
- •5.3.6. Метод іонної імплантації
- •5.4. Методи виготовлення канальних хвилеводів
- •6.1. Оптичні втрати та коефіцієнт затухання
- •6.2. Розсіяння
- •6.3. Абсорбція
- •6.4. Випромінювання
2.1. Оптичні явища на границі розділу двох діелектричних середовищ
В однорідному середовищі світло поширюється прямолінійно. Якщо світловий промінь, який поширюється в однорідному середовищі з деякою оптичною густиною, досягає границі другого середовища з іншою оптичною густиною, то він повністю або частково відіб’ється від границі розділу цих двох середовищ, а також повністю або частково проникне в друге середовище і трохи змінить свій напрямок поширення в порівнянні з напрямком поширення в першому середовищі.
2.2. Закони Снелла
У 1621 році голландський астроном і математик Уілброд ван Ройєн Снелл (Willebrod van Roijen Snell) вивів рівняння для опису проходження світла через різні матеріали, які стали називатися законами Снелла.
I. Закон відбивання: Відбитий промінь лежить в одній площині з падаючим променем і нормаллю до границі розділу двох середовищ в точці падіння променя, а кут відбивання рівний куту падіння по абсолютному значенню, але протилежний за знаком, оскільки вони розміщені по обидва боки від нормалі.
α = α′
II. Закон заломлення: Заломлений промінь лежить в одній площині з падаючим променем і нормаллю до границі розділу двох середовищ в точці падіння променя, а відношення синуса кута падіння до синуса кута заломлення є сталою величиною для заданих середовищ.
sin α / sin β = n2 / n1 = const
2.3. Повне внутрішнє відбивання
Якщо світло поширюється у середовищі з більшим показником заломлення і переходить у середовище з меншим показником заломлення, то на границі розділу цих двох середовищ буде спостерігатися явище заломлення, причому кут заломлення β світлових хвиль на границі розділу буде більшим за кут падіння α. Тобто, при n1 > n2 враховуючи закон заломлення: sin α < sin β. Якщо збільшувати кут падіння α, кут заломлення β буде також збільшуватись. При деякому куті падіння αгр виникне ситуація, коли кут заломлення β стане рівним π/2 (90°). При кутах падіння αгр < α < π/2 світло не буде проникати у друге середовище, а буде повністю відбиватись від границі розділу і повертатись у перше середовище. Це явище називається повним внутрішнім відбиванням (ПВВ), а кут падіння α = αгр, при якому це явище наступає, називається критичним кутом падіння або граничним кутом повного внутрішнього відбивання.
αгр = arcsin ( n2 / n1 )
Передача світлових хвиль по оптичному хвилеводу ґрунтується на явищі повного внутрішнього відбивання.
2.4. Закони Френеля
Розглядаючи явища і процеси при поширенні хвиль через границю розділу двох середовищ розрізняють хвилі TE- і TM-поляризацій. Хвилі TE-поляризації або TE-хвилі – це хвилі, вектор напруженості електричного поля яких перпендикулярний площині падіння. TM-хвилі – це хвилі, в яких вектор напруженості магнітного поля перпендикулярний площині падіння.
Якщо світлова хвиля падає на границю розділу двох середовищ, то в загальному випадку вона частково відіб’ється і частково пройде в друге середовище. Якщо амплітуда падаючої хвилі – А, відбитої – В, пройденої – С, то можна записати:
B = r × A, C = t × A
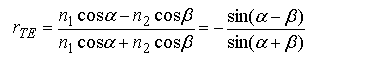
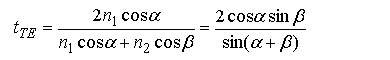
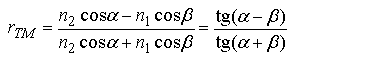
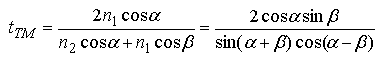
де r і t – амплітудні коефіцієнти відбивання і пропускання, які залежать від кута падіння і поляризації світла, і визначаються з формул Френеля:
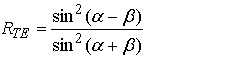
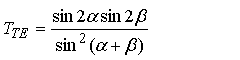
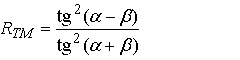
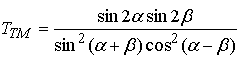
Формули Френеля описують співвідношення між амплітудами хвиль, однак у більшості випадків необхідно знати яким чином енергія падаючої хвилі розподіляється між відбитою і заломленою хвилями. Коефіцієнти відбивання і пропускання по інтенсивності (відбиваюча і пропускаюча здатність) границі розділу двох середовищ отримуються з використанням формул Френеля і мають наступний вигляд:
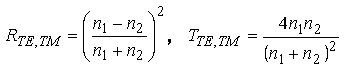
Для хвилі, яка падає нормально на границю розділу двох середовищ, вирази для R і T отримають простий вигляд:
![]()
Якщо на границю розділу падає хвиля, вектор напруженості електричного поля якої складає кут θ з площиною падіння, коефіцієнти R і T обчислюють за формулами:
Для
неполяризованого світла: