2. Робота випрямляча на активно-індуктивне навантаження

Режиму активно-індуктивного навантаження відповідають часові діаграми, які наведені на рис.4. Зауважимо, що розгляд процесів ведемо за умови ідеально спрямленого (постійного) струму I_d, тобто коли індуктивність в колі випрямленого струму безмежно велика L_d . Вказана умова характерна для випрямлячів середньої та великої потужності. Наявність індуктивності L_d" змінює характер залежностей i_d=f() та u_d=f(), які вище розглянуті за умови чисто активного навантаження. Режим роботи випрямляча характеризується наявністю в кривій випрямленої напруги u_d ділянок від’ємної полярності на інтервалах 0 - , -(+)..., а також ідеально спрямленою кривою струму навантаження i_d (рис.4а,б). Вказане обумовлюється впливом великої індуктивності, яка підтримує незмінним струм попереднього тиристора аж до вступу в роботу наступного. За таких умов струми тиристорів i_a1 , i_a2 мають вигляд імпульсів прямокутної форми (рис.4б). Очевидно, що на підставі першого закону Кірхгофа для вузла 0 i_a1 +i_{a 2}= i_d, або І_а1 + І_а2 =I_d ;за умови І_а1 = І_а2 = І_а середнє значення струму тиристора І_а зв’язане зі струмом навантаження I_d відношенням І_а= I_d/2. Зауважимо, що отримана залежність справедлива і для попереднього випадку роботи випрямляча.

Ділянки від’ємної полярності випрямленої напруги u_d зменшують її середнє значення U_d, яке, визначимо із виразу

. (3)

В результаті інтегрування отримаємо

U_d= U_d0соs . (4)

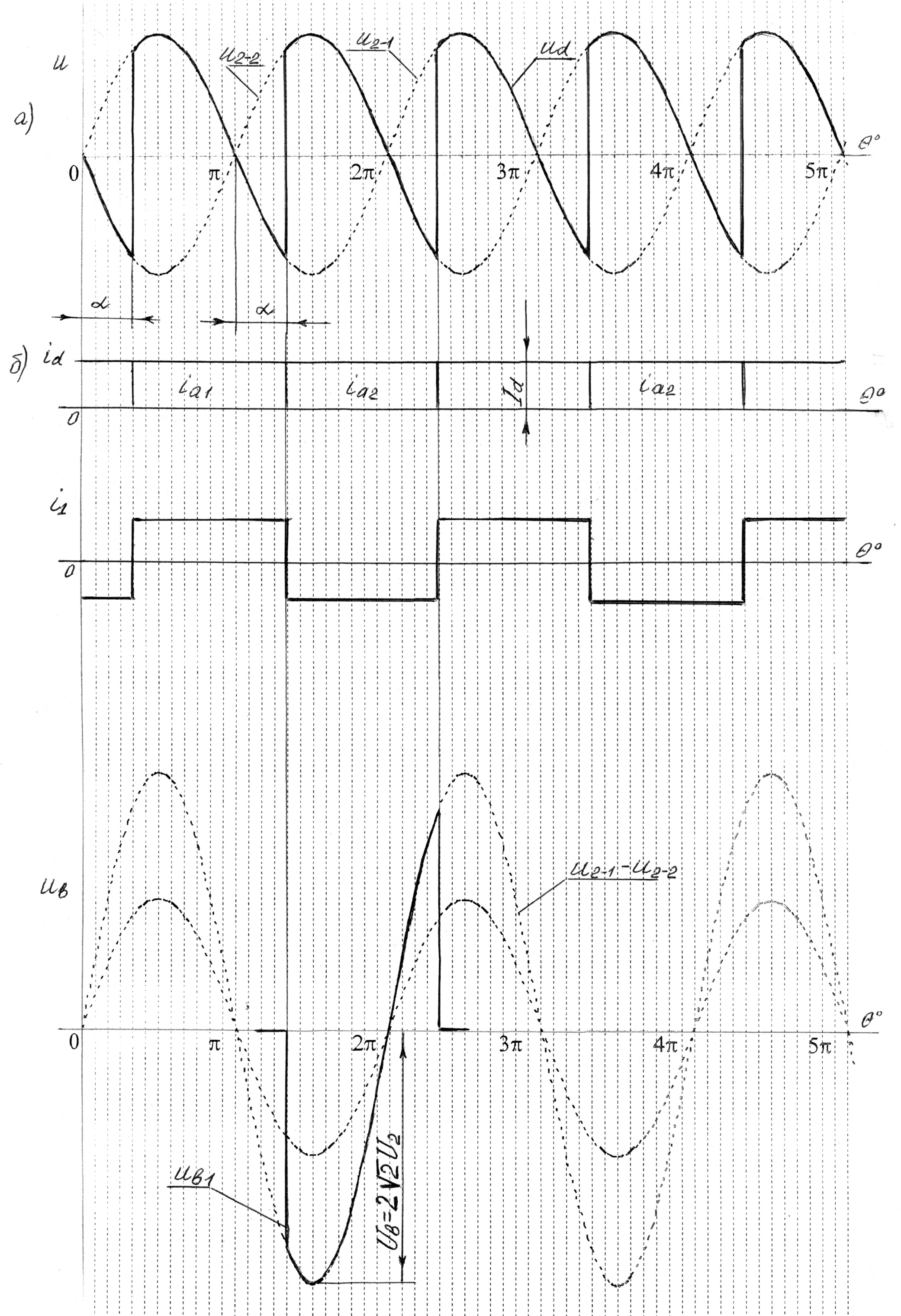
Рис.4. Часові діаграми струмів та напруг однофазного керованого випрямляча з виводом нульової точки за умов його роботи на активно - індуктивне навантаження та ідеального трансформатора схеми

Із наведених на рис.4 часових діаграм та отриманої формули очевидно, що кут  за означених умов можна змінювати від 0 лише до 90°. В графічному відображенні залежності (2), (4) наведені на рис.5 і, як зазначалося, носять назву регулювальних характеристик.

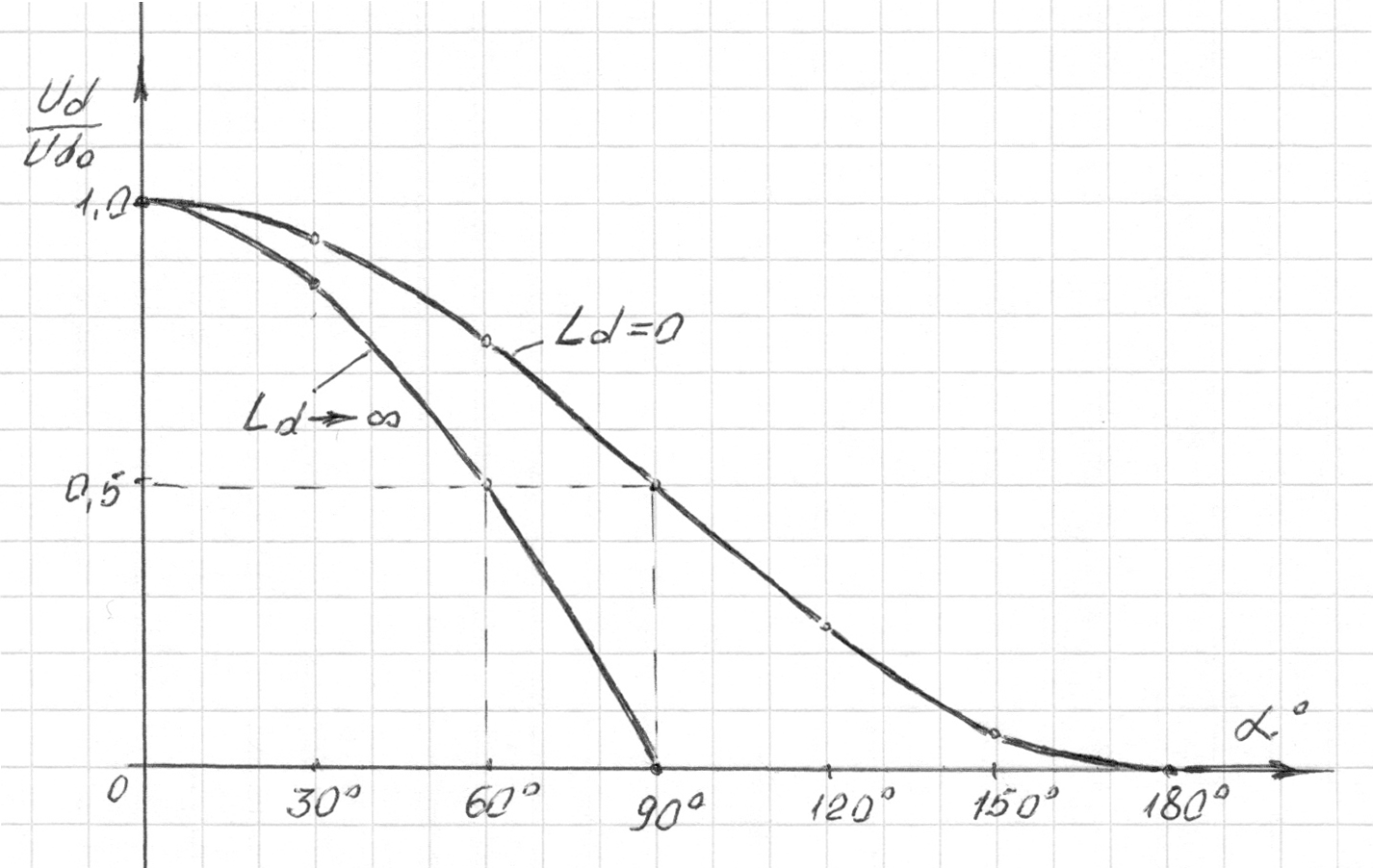
Рис.5. Регулювальні характеристики однофазних керованих випрямлячів

Регулювальні характеристики для проміжних значень > L_d>0 розташовуються між наведеними для граничних значень L_d.

Зворотна напруга тиристора u_в1 (в наведеному прикладі тиристора VS1) формується тільки напругою u_2-1 - u_2-2 =2 u₂. Її максимальне значення дорівнює U_в=2 U₂ , яке й слугує як розрахункове для вибору тиристорів.

Струм у первинній обмотці трансформатора є змінним , має прямокутну форму з амплітудою I_d/n.

3. Комутація струмів та зовнішні характеристики однофазних випрямлячів середньої та великої потужності

Розглянуті попередні випадки побудови кривих струмів та напруг випрямляча не враховували процесу комутації вентилів. Реальний трансформатор та мережа живлення мають певну індуктивність. Наявність індуктивності в електричному колі протидіє миттєвій зміні струму як вентиля, який вступає в роботу, так і вентиля, який виходить з роботи. Це призводить до того, що обидва тиристори схеми будуть одночасно у провідному стані протягом певного часу . Виникне процес комутації, який починається з моменту подачі імпульсу керування на черговий за порядком вступу в роботу тиристор і закінчується коли його струм досягне значення I_d, а струм тиристора, який виходить з роботи, досягне нульового значення (рис.6б).

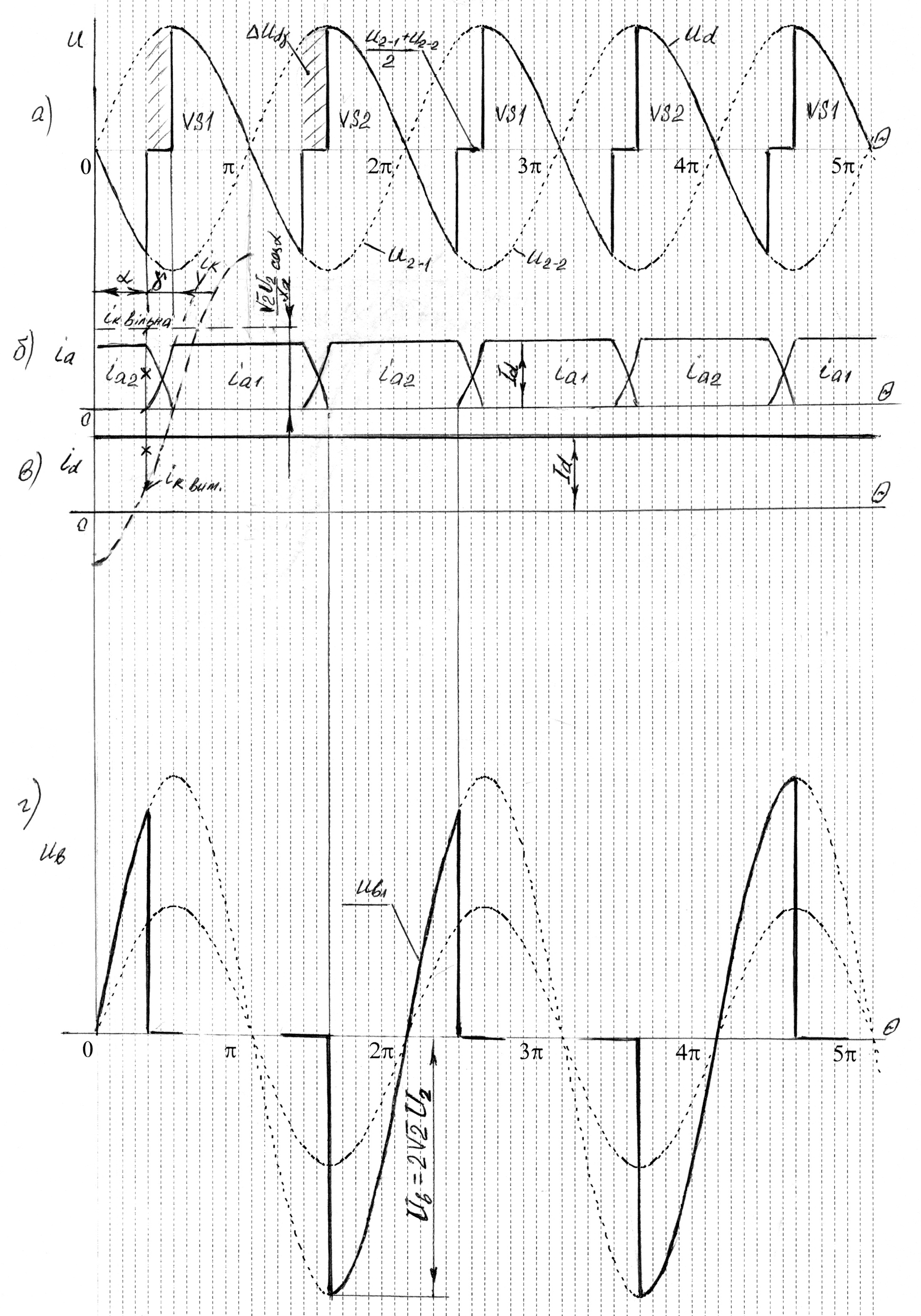
Рис.6. Часові діаграми струмів та напруг однофазного керованого випрямляча з виводом нульової точки з врахуванням процесів комутації

Наявність у провідному стані обох тиристорів схеми на етапі комутації призведе до того, що потенціал додатного полюса випрямляча буде визначатися півсумою вторинних напруг u_2-1 та u_2-2 . Оскільки ці напруги рівні і зсунуті по фазі між собою на 180°, то їхня півсума буде рівна нулю. Відповідно випрямлена напруга u_d = на ділянці комутації буде рівна нулю. Після завершення процесу комутації потенціал додатного полюса буде формувати напруга u_2-2 аж до початку наступної комутації. Середнє значення випрямленої напруги U_d буде меншим від такої ж напруги в режимі без комутації на величину комутаційного спаду напруги , область миттєвих значень яких заштрихована на рис.6а. Отже, для визначення середнього значення випрямленої напруги з врахуванням комутаційних процесів слід у формулі (4) врахувати комутаційний спад напруги

U_d = U_d0соs - . (5)

Величину знаходимо шляхом інтегрування виразу її миттєвого значення на інтервалі комутації     ,

= U₂ sin . (6)

В результаті інтегрування отримаємо

= . (7)

В формулу (7) входить різниця косинусів, яку слід визначити додатково. Для цього розглянемо комутаційний процес переходу струму, наприклад, з тиристора VS2 на тиристор VS1 детальніше. З моменту відкриття тиристора VS1 починається ділянка одночасної провідності обох тиристорів. Поступове зменшення до нуля струму і_а2 тиристора VS2 і зростання до величини I_d струму і_а1 тиристора VS1 здійснюється під впливом струму комутації i_к, який проходить у короткозамкнутому контурі під впливом обох вторинних напруг 2 u₂ (див. рис.2).

Струм в короткозамкнутому контурі обмежується сумарним опором обох обмоток трансформатора 2x_а та визначається за [1], як сума вимушеної і вільної складових

i_к = . (8)

На інтервалі комутації крива i_к = і_а1 визначає закон зміни струму тиристора VS1, а різниця I_d - i_к = і_а2 - закон зміни струму тиристора VS2. Ділянка комутації завершується, коли струм і_а1 досягне значення I_d , отже за умови i_к = I_d в момент отримаємо

I_d = .

Звідси визначаємо

= . (9)

Відповідно вираз (5) з врахуванням (7) та (9) набуде вигляду

U_d =U_d0соs - . (10)

Отриманий вираз описує сімейство зовнішніх характеристик керованого однофазного випрямляча з виводом нульової точки трансформатора, кожна з яких відповідає певному значенню кута . У графічному зображенні (рис.7) це будуть прямі лінії, нахил яких визначається величиною комутаційного спаду напруги .

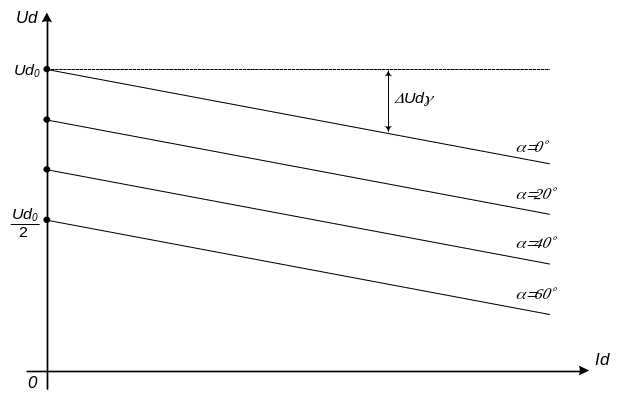
Рис.7. Зовнішні характеристики однофазного керованого випрямляча з виводом нульової точки трансформатора