Раздел 6 фильтрация

Фильтрация – движение жидкостей в пористых средах.

Опытный закон ламинарной фильтрации (дарси)

, (6.1)

где Q – фильтрационный расход, м³/с; S – полная площадь поперечного сечения потока, нормального к направлению движения жидкости, включающая поры и твердые частицы фильтрующего материала, м² ; i – гидравлический уклон; – линейные потери напора, м; L – длина участка, на котором отмечаются потери , м; k – коэффициент фильтрации, м/с, в справочниках [5, 6, 11] обычно дается в см/с (табл.6.1), зависит от материала пористой среды и вида фильтруемой жидкости.

Таблица 6.1

Фильтрующий материал	k, см/с
Гравий с размером зерен de = 4-7 мм	3,0-3,5
Мелкий гравий	3,0
Крупный чистый песок с de  2 мм	0,01-0,06
Мелкий чистый песок с de = 0,33-0,25 мм	0,001-0,006
Супесь	0,0003
Песчано-глинистый грунт	0,006-0,0001
Суглинок	110-4-610-5
Глины	(1-6)10-6
Глина плотная	10-7-10-10
Войлок	0,003-0,004

Коэффициент фильтрации для некоторых условий можно также определить расчетным путем. Так, например, для песчаных грунтов с известным размером зерен d_e (эффективный диаметр частиц песка) применяют формулу хазена

(6.2)

где  – кинематическая вязкость жидкости; с_m – коэффициент, зависящий от пористости m материала среды [5]:

Грунт	cm
Очень плотные пески	8,510-4
Пески средней пористости	1610-4

Скорость фильтрации через материал с поверхностью S

(6.3)

отличается от истинной скорости фильтрации

(6.4)

учитывающей пористость материала m (m = 0,3-0,5). при расчетах используют скорость v.

для безнапорной фильтрации при равномерном движении жидкости расход Q и скорость v определяют по формулам (6.1) и (6.3) при уклоне i водоупорного подстилающего слоя (ВПС).

Удельный расход – расход на единицу ширины потока l

. (6.5)

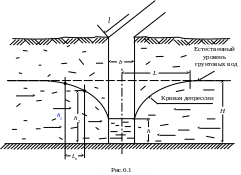
для неравномерного (плавноизменяющегося) движения жидкости при i = 0 приток жидкости к траншее (рис.6.1) с одной ее стороны определяется дебитом по формуле

(6.6)

где l – длина траншеи (или ширина потока); b – ширина траншеи; L – ширина зоны влияния траншеи; H – мощность водоносного слоя или статический напор, измеренный от уровня ВПС; h – глубина жидкости в траншее в период ее откачки или ордината кривой депрессии у стенки траншеи (динамический напор).

Если известны координаты h₁ и h₂ кривой депрессии, которая представляет собой свободную поверхность грунтовых вод (пьезометрическую линию) для широкого потока фильтрационной жидкости, то можно использовать формулу (6.7), например, для определения удельного расхода:

; (6.7)

где L_n – расстояние между сечениями с координатами h₁ и h₂.

Движение жидкости к совершенной скважине (скважина совершенна, если она проведена до ВПС и ее проницаемая поверхность ) радиусом r при безнапорной фильтрации характеризуется зависимостью для дебита:

(6.8)

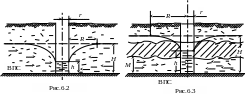
где h – глубина жидкости в колодце при ее откачке или ордината кривой депрессии у стенки колодца; R – радиус влияния колодца (рис.6.2).

При предварительных расчетах величину R можно определить по эмпирической зависимости Зихардта:

, (6.9)

где H, h – в метрах; k – в литрах в секунду.

Дебит артезианского колодца (колодец считается артезианским, если водоносный слой мощностью М сжат горными породами и имеет избыточное давление р по всей толще этого слоя) можно определить по формуле

(6.10)

где М – мощность водоносного пласта (рис 6.3).

дебит совершенного колодца, расположенного вблизи водоема, определяется зависимостью (6.8) при , где – расстояние от оси колодца до берега водоема.