Пример №5

Равноустойчивая стальная стойка ( ) длиной сжимается силой F = 40 кН (рисунок 12). Поперечное сечение составлено из двух неравнобоких уголков (рисунок 13), материал Ст. 3,

Необходимо:

1. Определить из условия устойчивости номер уголка.

2. Найти критическую силу и коэффициент запаса устойчивости.

3. Определить из условия равноустойчивости размер с сечения.

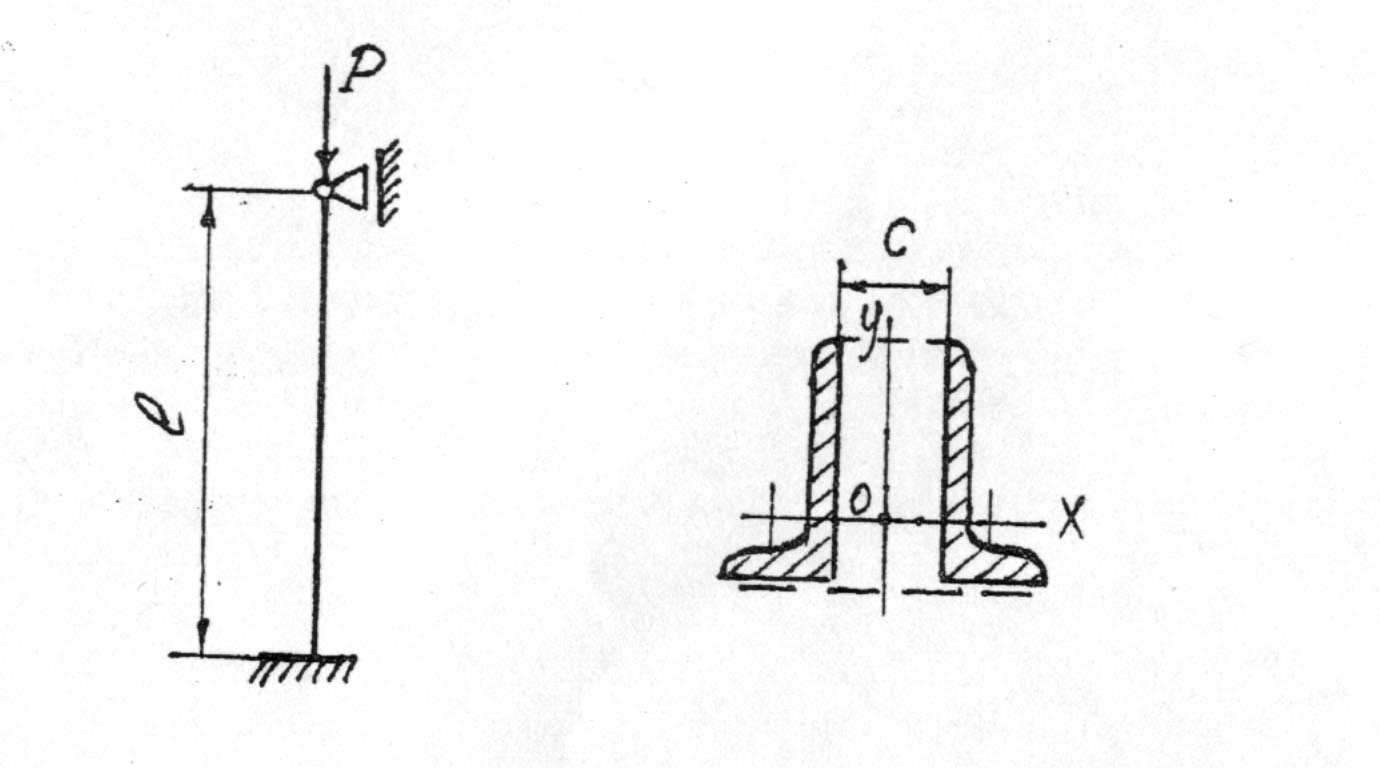
Рисунок 12 − Схема равноустойчивой стальной стойки	Рисунок 13 − Поперечное сечение стойки

Решение

Решение задачи осуществляют методом постепенного приближения. Зададимся первым значением коэффициента снижения основного допускаемого напряжения ₁ = 0,5.

Из условия устойчивости находим требуемую площадь поперечного сечения А.

.

Площадь уголка .

По приложению таблицы 9 примем уголок 40254 с площадью и радиусом инерции .

Радиус инерции сечения относительно оси Х равен радиусу инерции уголка:

.

Гибкость стойки =

Здесь коэффициент приведения длины для данной стойки .

Из приложения (таблица 3) по гибкости определяем , не совпадающее с , поэтому на следующем этапе примем второе значение  .

.

А = , .

Примем уголок 50324, , .

по таблице .

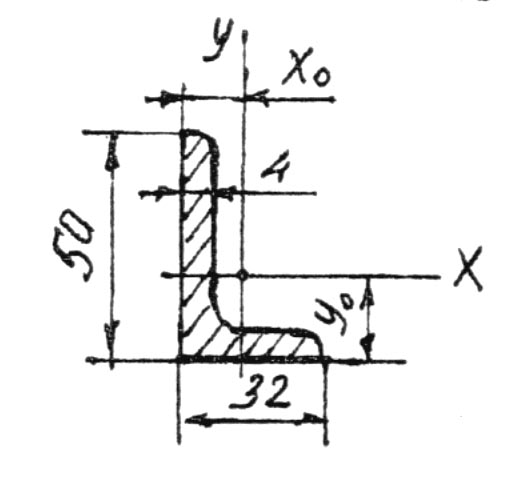
Поскольку , окончательно принимаем уголок 50324 (рисунок 14) со следующими данными:

,		Рисунок 14 − Схема принятого уголка
,
.

Определяем критическую силу.

Так как гибкость для (Ст. 3), то критическую силу вычисляем по формуле Л. Эйлера.

Коэффициент запаса устойчивости .

Вычисляем размер с из условия равенства главных центральных моментов инерции сечения.

,

Окончательно принимаем с = 11 мм.

Список использованной и рекомендуемой литературы

1. Балакин, В.А. Механика материалов: Практич. пособие к решению контрольных и расчетно-графических работ по одноим. курсу для студентов днев. и заоч. форм обучения спец. мех.-техн. и машиностроит. фак. /В.А.Балакин, И.Н.Литвиненко, А.А.Иванов. – Гомель: ГГТУ им. П.О.Сухого, 2004. – 79 с.

2. Дарков, А.В., Шпиро, Г.С. Сопротивление материалов: Учеб. для втузов. – 5-е изд., перераб. и доп. – М.: Высш. школа, 1989. – 624 с.

3. Методические указания к контрольным работам по сопротивлению материалов для студентов-заочников технологических специальностей / сост. А.В. Минченко, А.В. Карпушко // Витебск: УО ВГТУ, 2001.– 52 с.

4. Михайлов, А.В. Сопротивление материалов: Учебник для техникумов. – М.: Стройиздат, 1989. – 352 с.

5. Степин, П.А. Сопротивление материалов: Учеб. для немашиностроит. спец. вузов. – 8-е изд. – М.: Высш. школа, 1988. – 367 с.

6. Феодосьев, В.И. Сопротивление материалов: Учеб. для вузов. – 9-е изд., перераб. – М.: Наука, 1986. – 512 с.