3.6.Колебания круглой мембраны.
Применим метод решения задачи о колебаниях прямоугольной мембраны к колебаниям круглой мембраны. Пусть мембрана в состоянии покоя занимает круг радиуса R с центром в начале координат. Введем полярные координаты r и φ:
x=rcos φ, y=rsin φ.
Выполняя замену переменных u(x,y,t) u(r,φ,t) уравнение колебаний мембраны приводятся к виду
(131)
Граничные условие будет иметь вид
Начальные условия
Будем рассматривать только осесимметричные колебания мембраны, т.е. начальные условия не должны зависеть от угла φ. Очевидно, что в любой момент времени скорости и отклонения точек будут зависеть от угла, поэтому наша задача упрощается:
(132)
Граничные условия
Начальные условия
Будем искать решение в виде
(133)
Из краевого условия сразу находим
U(R)=0
Подставляя (133) в уравнение, получаем
разделим на UT
(134)
В результате приходим к уравнениям
(135)
(136)
В последнем сделаем
замену
:
Подставляя в наше уравнение, получаем
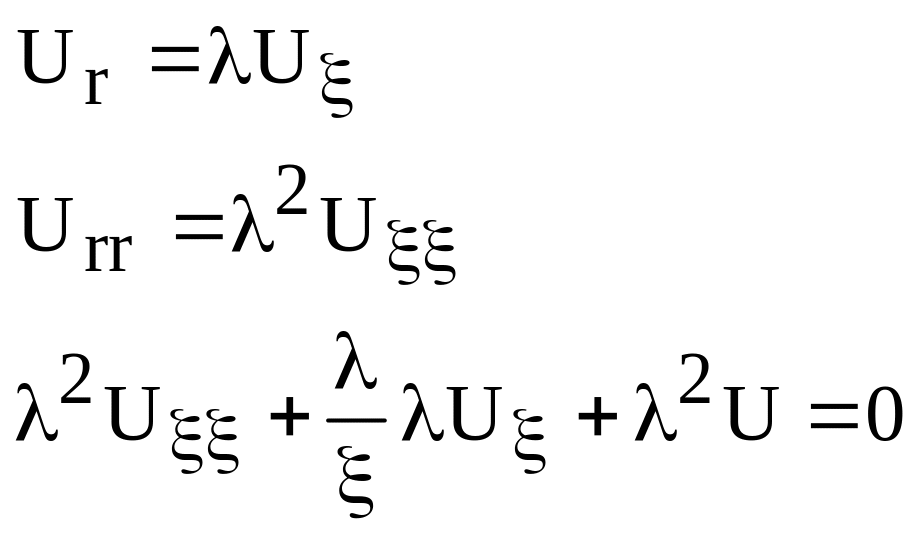
(137)
Получившееся уравнение является частным случаем уравнения Бесселя:
(138)
Решениями последнего уравнения при заданном k называется бесселевыми функциями порядка k (цилиндрическими функциями).
Найдем решение уравнения (138). Очевидно, что оно имеет особую точку при x=0, поэтому его решение будем искать в виде степенного ряда. Для этого преобразуем его к виду:
(139)
Записываем ряд:
(140)
Подставляя (140) в (139) и приравнивая коэффициенты при каждой степени x нулю, получим систему уравнений
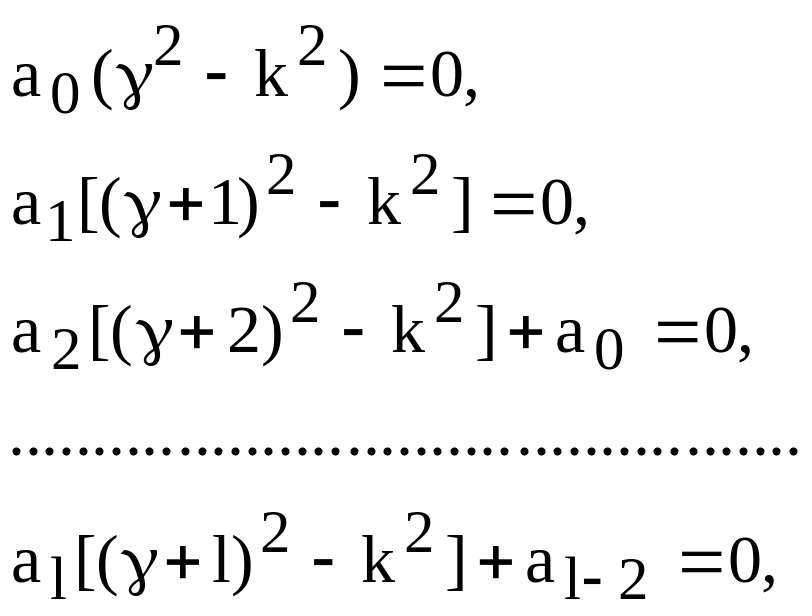(141)
Где l=2,3…
Предполагая, что
,
находим
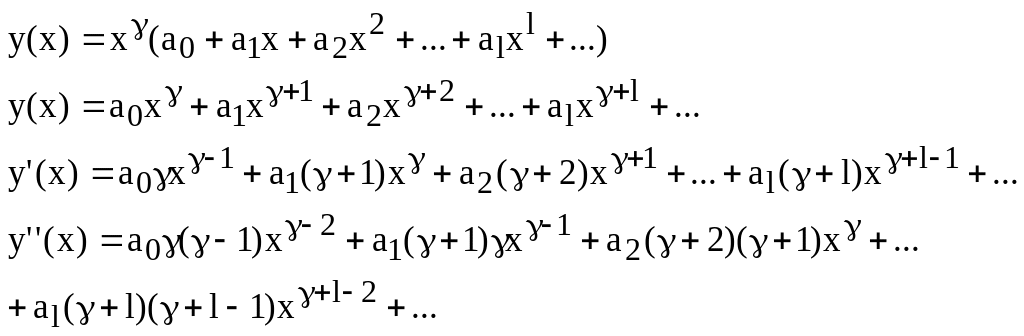
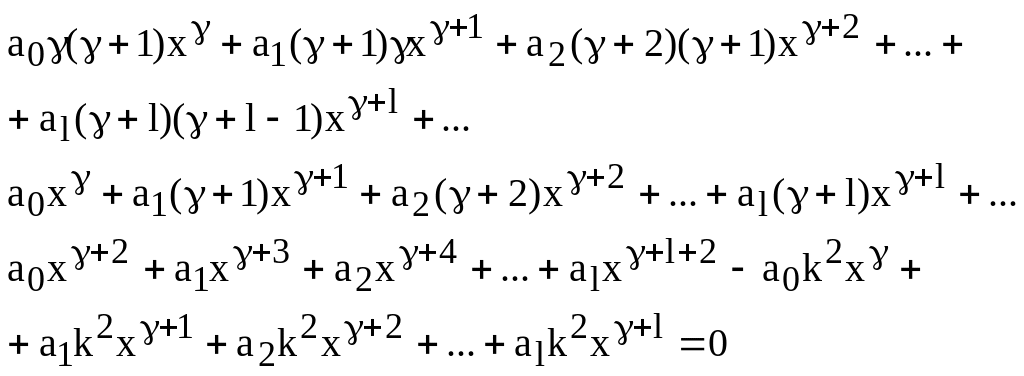
Из второго уравнения
(141) находим, что
=0.
преобразуем l-е
уравнение в системе (141).
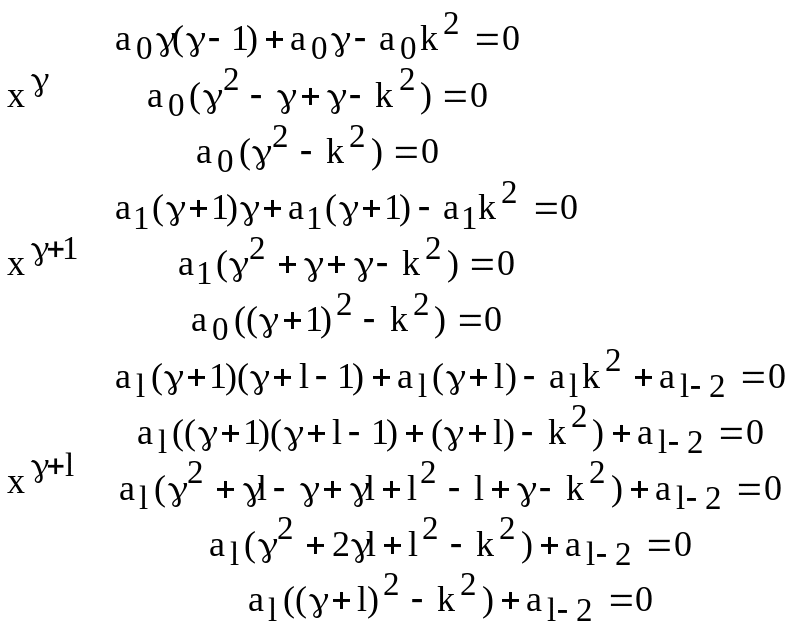
(142)
Отсюда получаем рекуррентную формулу:
(143)
С учетом найденного
=0
делаем вывод, что все нечетные коэффициенты
равны нулю. Очевидно, что при
решение обращается в бесконечность при
x=0.
будем рассматривать случай
.
В результате, для четных коэффициентов
получаем
(144)
Применяя эту формулу m-1 раз, получим
(145)
Полагая,
Получаем
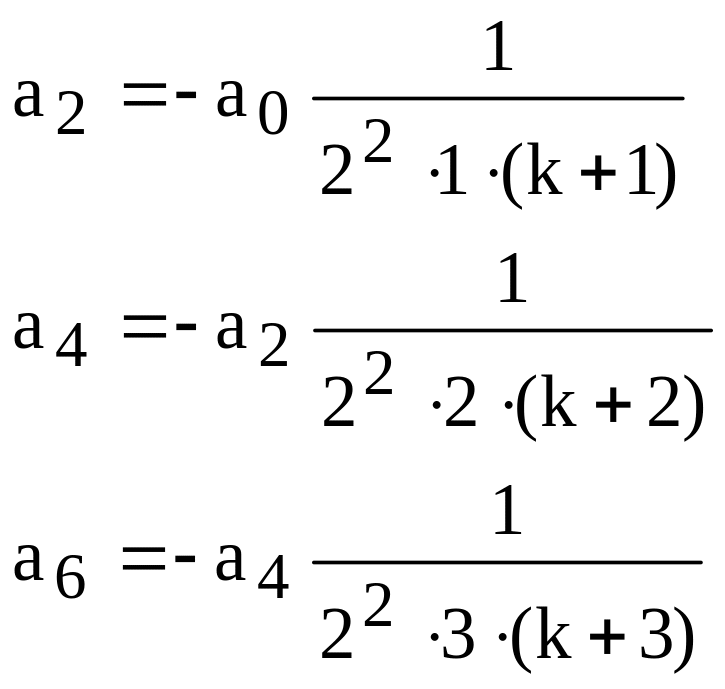
(146)
В результате,
полученное решение
называется функцией Бесселя первого
рода k-ого
порядка и имеет вид:
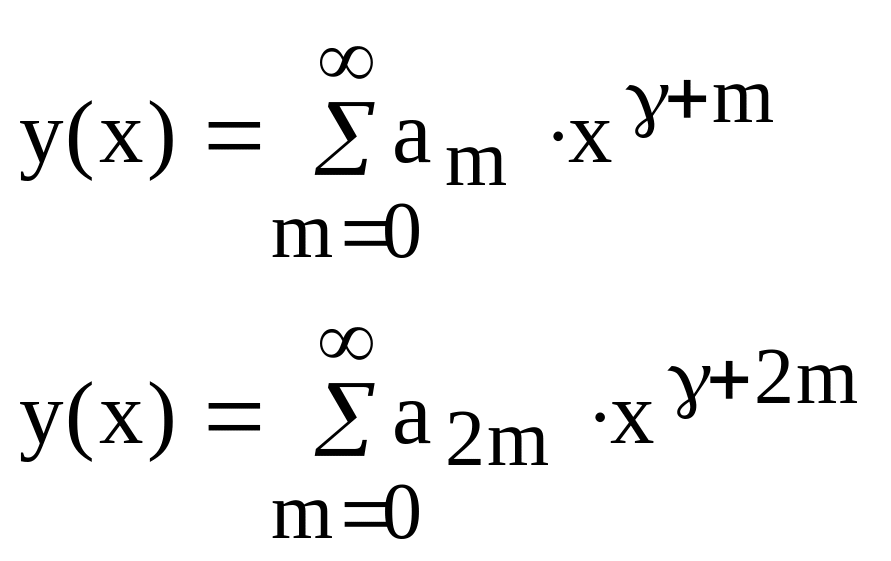
(147)