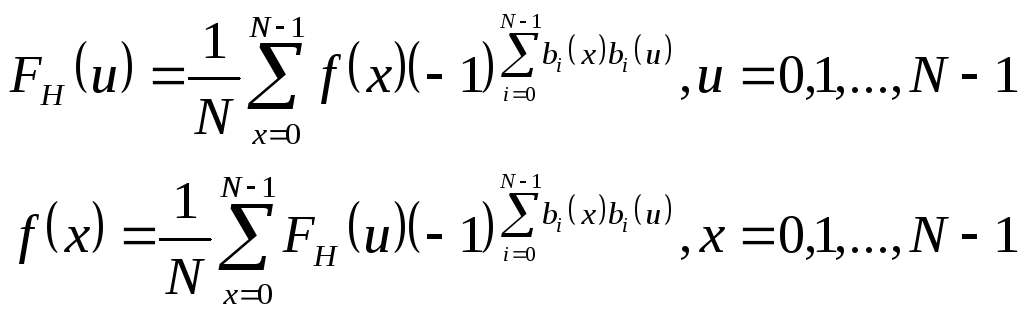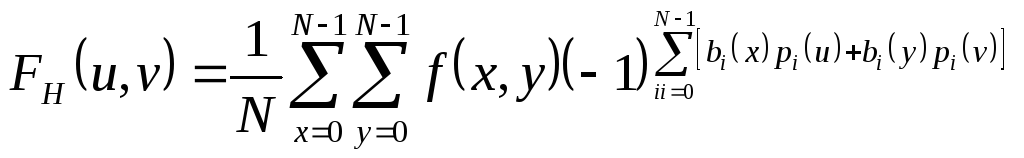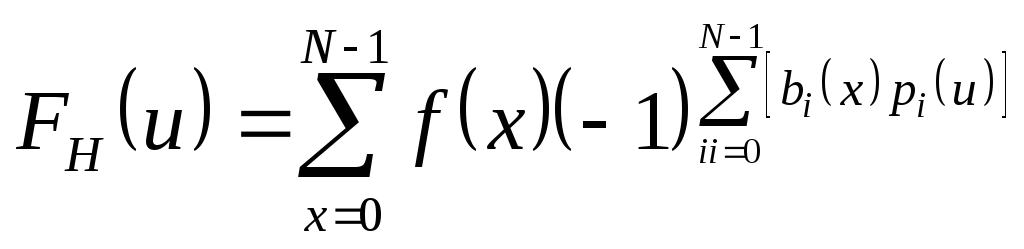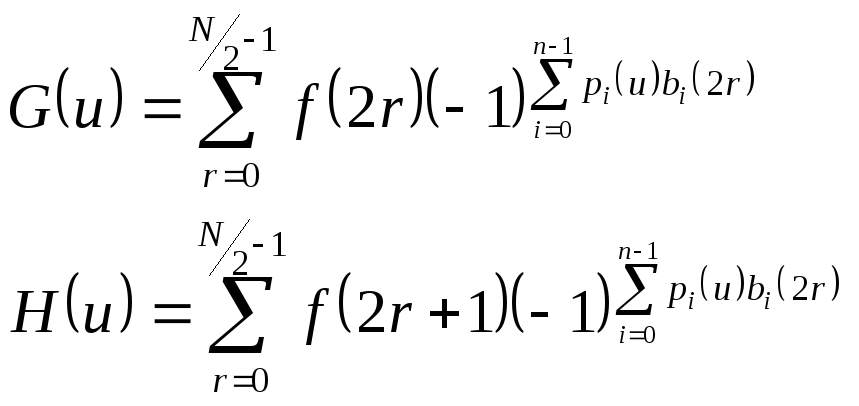8.5.2 Преобразование Адамара

Если функция

(8.98)

используется в качестве ядра обобщенного преобразования (8.10), то такое преобразование известно как преобразование Адамара. Пара преобразований Адамара - следующая:

(8.99) (8.100)

где N - это число элементов выборки, равное, аn- целое положительное число. Аргументаналогичен используемому в преобразовании Уолша.

Некоторые свойства матриц Адамара (H) полезны при их генерации:

Свойство 1Матрица Адамара - это квадратная матрица строки (и столбцы) которой ортогональны и содержат элементы равные либо +1, либо -1. Для матрицы

(8.101) (8.102)

Наименьшая матрица Адамара (при N=2) определяется как

(8.103)

Свойство 2

(8.104)

Свойство 3

Следующий простой рекурсивный алгоритм может использоваться для создания матриц Адамара:

(8.105)

где ипредставляют собой соответственно матрицы размераN и2N. Если использовать "+" и "-" в качестве "+1" и "-", то в упрощенной нотации получаем:

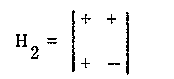
И то же самое рекурсивное соотношение позволяет записать:

Матрица H формируется рекурсивным алгоритмом неупорядоченно (т.е. неупорядоченно множество изменений знака). Эта ситуация может быть изменена путем внесения изменений в ядро, которые будут обсуждаться позднее.

Двумерное преобразование Адамара может быть записано как:

(8.108)

где - это преобразование Адамара от, а- симметричная матрица Адамара, размера. Обратное преобразование Адамара отесть

(8.109)

или

после подстановки из уравнения 8.108. Используя соотношение 8.101 получаем:

(8.110)

и также

(8.111)

что формирует пару преобразований Адамара с 8.108.

Чтобы расположить последовательность в порядке возрастания запишем ядро прямого преобразования как:

(8.112)

Тогда преобразование Адамара принимает вид:

(8.112)

где и xиu представлены в двоичной форме.определяется как

(8.114)

и

(8.115)

где представляет собой крайний левый битu;- следующий слева битuи т.д. Суммирование в формулах 8.114 и 8.115 выполняются согласно арифметике по модулю два. Аналогичные рассуждения применимы и к.

Пример Для одномерного преобразования Адамара вычислить значения упорядоченного ядра при.

Решение Приu=2 (0 1 0 в двоичном представлении) их = 6 (1 1 0) имеем:

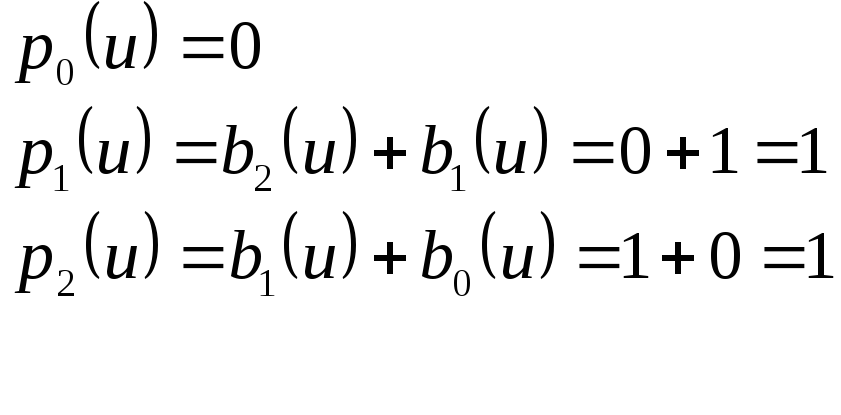
При u=5 (1 0 1 в двоичном представлении) и 4 = 6 (1 0 0) имеем:

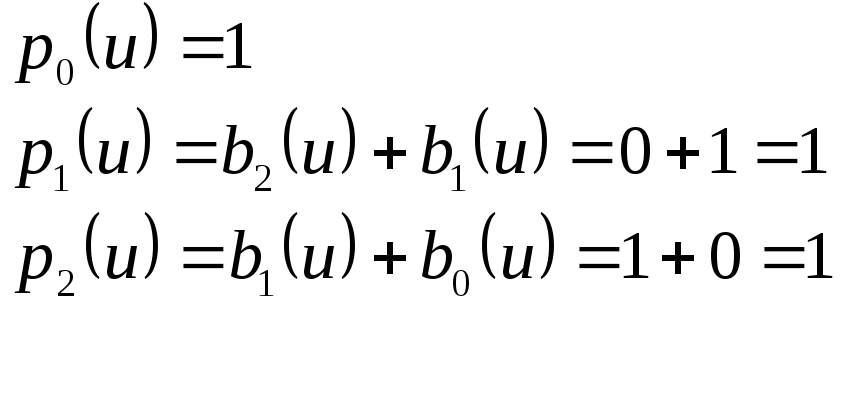
и так далее, пока упорядоченное ядро преобразования Адамара не будет построено как показано в 8.116.

Сравнивая 8.106 и 8.116 мы можем убедиться, что последовательность из 8.116 упорядочена.

Как видно из 8.112, ядро двумерного преобразования Адамара сепарабильно. Т.о.:

(8.117)

где - одномерное преобразование Адамара. Аналогично двумерному преобразованию Фурье, одномерное преобразование Адамара может быть использовано для вычисления двумерного, а также возможно использование быстрого вычислительного алгоритма. Аналогично преобразованию Фурье, преобразование Адамара записывается как

(8.118)

и может быть представлена в виде суммы двух рядов

(8.119)

Заметив, что

(8.120)

и

для четных х для нечетных

(8.121)

имеем

(8.122)

или

(8.123)

поскольку мы знаем, что по определению равно 1. Зная уравнения 8.120 и 8.121 можно переписать уравнение 8.118 в следующей форме:

(8.124)

Уравнение 8.119 преобразуется в

		(8.125)
	(8.126)

где

(8.127) (8.128)

и

(8.129)

Знак H(u)определяемыйположителен прии отрицателен при.