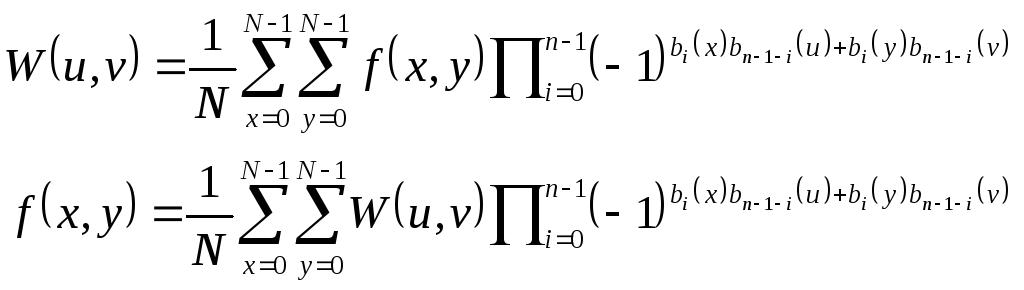8.5 Другие дискретные преобразования изображений

Преобразование Фурье - только одна из методик преобразования, используемых при обработке изображений. Другие методы преобразования также показали себя очень эффективными. Это - преобразование Уолша, преобразование Адамара, преобразование Карунена-Лева и т.д. Как и преобразование Фурье, все эти преобразования обратимы; причем как прямое, так и обратное преобразование могут применяться к непрерывным интегрируемым функциям, что делает возможным обработку изображений в домене преобразования.

8.5.1 Преобразование Уолша

Если функция

(8.88)

используется в качестве ядра преобразования, то такое преобразование известно как преобразование Уолша. Т.е. преобразование Уолша - это

(8.89)

где N - это число точек выборки, являющееся степенью двойки,представляет собой k-ое битовое представлениеz, где нулевой бит является младшим. Например, если,(1 1 0 1 в битовом представлении), то. Ядро для

Подстановкой в выражение выше мы получаем значение ядра для случая, обведенного кружком на рисунке 8.51

, которое является отрицательным значением. На рисунке 8.51 можно видеть, что ядро является симметричным и ортогональным, поэтому ядро обратного преобразованияидентично ядру прямого за исключением постоянного множителя. Т.о. мы имеем

(8.90)

и обратное преобразование Уолша есть

(8.91)

Начнем с наименьшего N(N = 2) и посмотрим, как строится массив ядер преобразования Уолша. КогдаN = 2 (илиn = 1), уравнение 8.88 превращается в

Получаемое при этом простейшее ядро преобразования Уолша показано на рисунке 8.53. Для N = 4 (илиn = 2), уравнение 8.88 превращается в

Соответствующее ядро преобразования Уолша показано на рисунке 8.53. Аналогичный процесс арифметической подстановки позволяет получить ядра для N = 8 (илиn = 3) иN = 16 (илиn = 4), показанные на рисунках 8.54 и 8.51 соответственно.

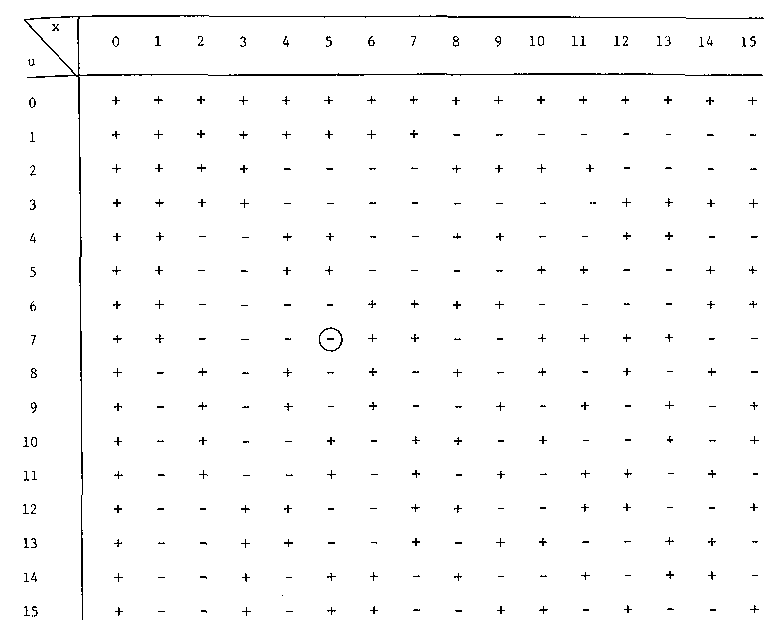
Рисунок 8.51 Значения ядра преобразования Уолша при N=16

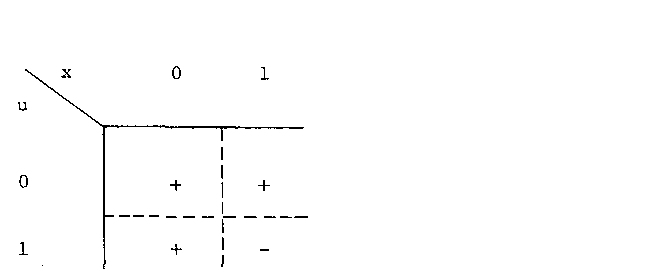
Рисунок 8.52 Значения ядра преобразования Уолша при N = 2

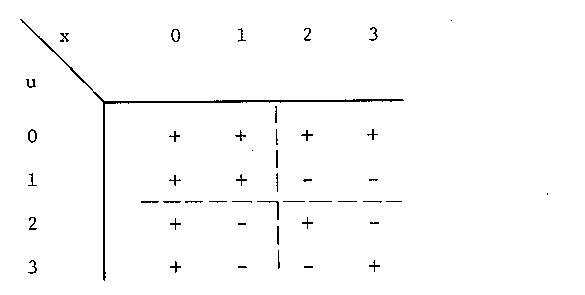
Рисунок 8.53 Значения ядра преобразования Уолша при N = 4

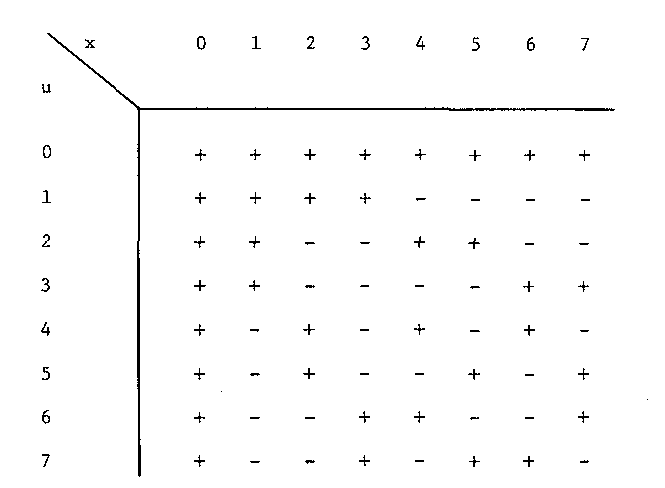
Рисунок 8.54 Значения ядра преобразования Уолша при N = 8

Расширяя преобразование Уолша на двумерный случай, мы получаем пару ядер преобразований, показанную ниже:

(8.92)

и

(8.93)

Как уже обсуждалось для уравнения 8.90, одно и то же ядро может быть использовано как для прямого, так и для обратного преобразования Уолша, а потому

(8.94) (8.95)

Уравнения 8.94 и 8.95 демонстрируют что один алгоритм может быть использован как для прямого, так и для обратного двумерного преобразования Уолша. Из них также вытекает, что ядра исимметричны и сепарабельны.

(8.96) (8.97)

где

а

Таким образом, как прямое, так и обратное двумерные преобразования Уолша могут быть выполнены путем последовательного применения одномерных преобразований, причем для всех этих вычислений может использоваться один и тот же алгоритм. Процедура вычислений будет такой же, как и для преобразования Фурье. Аналогично БПФ можно записать и быстрый алгоритм преобразования Уолша. Если множители и т.д. уже вычислены, то алгоритмы БПФ и БПУ (быстрого преобразования Уолша) будут одинаковы, а реализация БПФ на Фортране, приведенная на рисунке 8.48 может быть использована для БПУ с удалениемU, WиPIи заменой "COMPLEX" на "REAL" (см. рисунок 8.55).

Рисунок 8.55 Реализация БПУ на Фортране